Difference between revisions of "Aufgaben:Exercise 1.4Z: Representation of Oscillations"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/ Allgemeines Modell der Modulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choi…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID969__Mod_Z_1_4.png|right|]] |
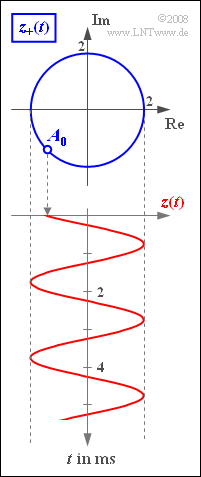
| + | Betrachtet wird eine harmonische Schwingung $z(t)$, die zusammen mit dem zugehörigen Signal $z_+(t)$ in der Grafik dargestellt ist. | ||
| + | |||
| + | Diese Signale können mathematisch wie folgt beschrieben werden: | ||
| + | $$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}) \\ = A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm}, \\ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t}$$ | ||
| + | Die zwei Amplitudenparameter $A_T$ und $A_0$ sind jeweils dimensionslos, der Phasenwert $ϕ_T$ soll zwischen $\text{±π}$ liegen und die Laufzeit τ ist nicht negativ. | ||
| + | |||
| + | Beachten Sie weiter, dass $ϕ_T$ in obiger Gleichung mit positivem Vorzeichen erscheint. Unter Anmerkungen zur Nomenklatur finden Sie eine Begründung für die unterschiedliche Verwendung von $φ_T$ und $ϕ_T = – φ_T$. | ||
| + | |||
| + | |||
Revision as of 16:24, 27 December 2016
Betrachtet wird eine harmonische Schwingung $z(t)$, die zusammen mit dem zugehörigen Signal $z_+(t)$ in der Grafik dargestellt ist.
Diese Signale können mathematisch wie folgt beschrieben werden: $$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}) \\ = A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm}, \\ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t}$$ Die zwei Amplitudenparameter $A_T$ und $A_0$ sind jeweils dimensionslos, der Phasenwert $ϕ_T$ soll zwischen $\text{±π}$ liegen und die Laufzeit τ ist nicht negativ.
Beachten Sie weiter, dass $ϕ_T$ in obiger Gleichung mit positivem Vorzeichen erscheint. Unter Anmerkungen zur Nomenklatur finden Sie eine Begründung für die unterschiedliche Verwendung von $φ_T$ und $ϕ_T = – φ_T$.
Fragebogen
Musterlösung