Difference between revisions of "Aufgaben:Exercise 2.8: Asymmetrical Channel"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Hüllkurvendemodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |t…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1038__Mod_A_2_8.png|right|]] |
| + | Ein cosinusförmiges Quellensignal $q(t)$ mit der Amplitude $A_N$ und der Frequenz $f_N$ wird ZSB–amplitudenmoduliert, so dass für das modulierte Signal gilt: | ||
| + | $$ s(t) = ( q(t) + A_{\rm T}) \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | ||
| + | Der Übertragungskanal weist lineare Verzerrungen auf. Während sowohl das untere Seitenband als auch der Träger unverfälscht übertragen werden, wird das obere Seitenband (bei der OSB-Frequenz $f_T + f_N$) mit dem Dämpfungsfaktor $α_O = 0.25$ gewichtet. | ||
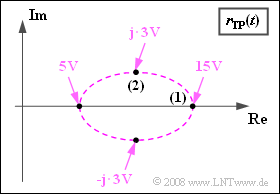
| + | Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals $r_TP(t)$ in der komplexen Ebene. Wertet man das Signal $r(t)$ mit einem idealen Hüllkurvendemodulator aus, so erhält man ein Sinkensignal $υ(t)$, das wie folgt angenähert werden kann: | ||
| + | $$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )- ...$$ | ||
| + | Für diese Messung wurde die Nachrichtenfrequenz $f_N = 2 kHz$ benutzt. | ||
| + | |||
| + | In der Teilaufgabe g) soll das Signal–zu–Stör–Leistungsverhältnis (SNR) wie folgt berechnet werden: | ||
| + | $$ \rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$ | ||
| + | Hierbei bezeichnen $P_{υ1} = α^2 · P_q$ und $P_ε$ die „Leistungen” der beiden Signale: | ||
| + | $$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ | ||
| + | $$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://en.lntwww.de/Modulationsverfahren/H%C3%BCllkurvendemodulation Kapitel 2.3]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 19:11, 1 January 2017
Ein cosinusförmiges Quellensignal $q(t)$ mit der Amplitude $A_N$ und der Frequenz $f_N$ wird ZSB–amplitudenmoduliert, so dass für das modulierte Signal gilt: $$ s(t) = ( q(t) + A_{\rm T}) \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$ Der Übertragungskanal weist lineare Verzerrungen auf. Während sowohl das untere Seitenband als auch der Träger unverfälscht übertragen werden, wird das obere Seitenband (bei der OSB-Frequenz $f_T + f_N$) mit dem Dämpfungsfaktor $α_O = 0.25$ gewichtet.
Die Grafik zeigt die Ortskurve, also die Darstellung des äquivalenten Tiefpass–Signals $r_TP(t)$ in der komplexen Ebene. Wertet man das Signal $r(t)$ mit einem idealen Hüllkurvendemodulator aus, so erhält man ein Sinkensignal $υ(t)$, das wie folgt angenähert werden kann: $$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )- ...$$ Für diese Messung wurde die Nachrichtenfrequenz $f_N = 2 kHz$ benutzt.
In der Teilaufgabe g) soll das Signal–zu–Stör–Leistungsverhältnis (SNR) wie folgt berechnet werden: $$ \rho_{v } = \frac{P_{v 1}}{P_{\varepsilon }} \hspace{0.05cm}.$$ Hierbei bezeichnen $P_{υ1} = α^2 · P_q$ und $P_ε$ die „Leistungen” der beiden Signale: $$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ $$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$
Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.3.
Fragebogen
Musterlösung