Aufgaben:Exercise 3.5: PM and FM for Rectangular Signals

• Return to book

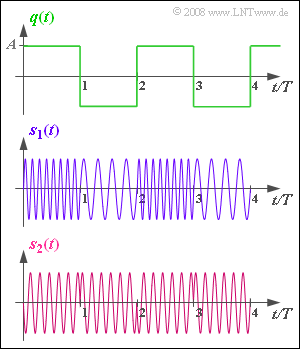
Wir gehen von einem bipolaren und rechteckförmigen Quellensignal $q(t)$ aus, welches im oberen Diagramm dargestellt ist.

Dieses kann nur die beiden Signalwerte $±A = ±2 V$ annehmen und die Dauer der positiven und negativen Rechtecke ist jeweils $T = 1 ms$. Die Periodendauer von $q(t)$ ist demzufolge $T_0 = 2 ms$.

Die Signale $s_1(t)$ und $s_2(t)$ zeigen zwei Sendesignale bei Winkelmodulation (WM), die jeweils in der Form $$s(t) = A_{\rm T} \cdot \cos (\psi (t) )$$ darstellbar sind. Hierbei unterscheidet man zwischen der Phasenmodulation (PM) mit der Winkelfunktion $$\psi(t) = \omega_{\rm T} \cdot t + \phi(t)$$ $$ = \omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t)$$ und der Frequenzmodulation (FM), bei der die Augenblicksfrequenz linear mit $q(t)$ zusammenhängt: $$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi}, \hspace{0.3cm} \omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}= \omega_{\rm T} + K_{\rm FM} \cdot q(t)\hspace{0.05cm}.$$ $K_{PM}$ und $K_{FM}$ bezeichnen dimensionsbehaftete, durch die Realisierung des PM– bzw. FM–Modulators vorgegebene Konstante. Der Frequenzhub $Δf_A$ gibt die maximale Abweichung der Augenblicksfrequenz von der Trägerfrequenz an.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.1 und Kapitel 3.2. Im Vorgriff auf das Kapitel 4 sei erwähnt, dass man die Phasenmodulation bei digitalem Eingangssignal auch als PSK (Phase Shift Keying) und entsprechend die Frequenzmodulation als FSK (Frequency Shift Keying) bezeichnet.

Fragebogen

1

Welches der Signale ist durch eine PM, welches durch eine FM entstanden?

	$s_1(t)$ beschreibt eine Phasenmodulation.
	$s_1(t)$ beschreibt eine Frequenzmodulation.

2

Wie groß ist die Trägerphase $ϕ_T$, die man mit $q(t) = 0$ messen könnte?

$ϕ_T$ = $Grad$

3

Welche Trägerfrequenz (bezogen auf 1/T) wurde bei den Grafiken verwendet?

$f_T · T$ =

4

Das Phase des PM–Signals ist $±90°$. Wie groß ist die Modulatorkonstante?

$K_{PM}$ = $V^{-1}$

5

Wie groß ist der Frequenzhub $Δf_A$ des FM–Signals, bezogen auf 1/T?

$Δf_A · T$ =

6

Wie groß ist die FM–Modulatorkonstante?

$K_{FM}$ = $(Vs)^{-1}$

Musterlösung

Solution

1. Bei einem rechteckförmigen (digitalen) Quellensignal erkennt man die Phasenmodulation (PM) an den typischen Phasensprüngen – siehe Signalverlauf $s_2(t)$. Die Frequenzmodulation (FM) weist dagegen zu den verschiedenen Zeiten unterschiedliche Augenblicksfrequenzen wie bei $s_1(t)$ auf ⇒ $\underline{Antwort 2}$.

2. Mit $q(t) = 0$ erhält man entsprechend den gegebenen Gleichungen sowohl für PM als auch für FM $$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t ) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \phi_{\rm T} \hspace{0.15cm}\underline {= 0}\hspace{0.05cm}.$$

3. Die Trägerfrequenz $f_T$ kann direkt nur aus dem PM–Signal $s_2(t)$ ermittelt werden. Bei der FM eines bipolaren Quellensignals tritt $f_T$ nicht auf. Durch Abzählen der Schwingungen von $s_2(t)$ im Zeitintervall T erkennt man, dass $f_T · T = 6$ verwendet wurde.

4. Der Amplitudenwert $A = 2 V$ führt zur Phase $90°$ bzw. $π/2$ (Minus–Sinusverlauf). Daraus folgt: $$K_{\rm PM} = \frac {\pi /2}{2\,{\rm V}} \hspace{0.15cm}\underline {= 0.785\,{\rm V}^{-1}} \hspace{0.05cm}.$$

5. Die Grafik $s_1(t)$ zeigt, dass innerhalb eines Zeitintervalls T entweder 4 oder 8 Schwingungen auftreten: $$4 \le f_{\rm A}(t) \cdot T \le 8\hspace{0.05cm}.$$ Unter Berücksichtigung der Trägerfrequenz $f_T · T = 6$ ergibt sich für den (normierten) Frequenzhub: $$\Delta f_{\rm A} \cdot T \hspace{0.15cm}\underline {=2}\hspace{0.05cm}.$$

6.Der Frequenzhub kann auch wie folgt dargestellt werden: $$\Delta f_{\rm A} = \frac {K_{\rm FM}}{2\pi}\cdot A \hspace{0.05cm}.$$ Mit $Δf_A · T = 2$ erhält man somit $$K_{\rm FM} = \frac {2 \cdot 2\pi}{A \cdot T}= \frac {4\pi}{2\,{\rm V} \cdot 1\,{\rm ms}}\hspace{0.15cm}\underline {= 6283 \,{\rm V}^{-1}{\rm s}^{-1}} \hspace{0.05cm}.$$