Difference between revisions of "Aufgaben:Exercise 3.10: Noise Power Calculation"
| Line 12: | Line 12: | ||
Die Rauschleistungsdichte nach der FM–Demodulation lautet mit dem Frequenzhub $Δf_A$: | Die Rauschleistungsdichte nach der FM–Demodulation lautet mit dem Frequenzhub $Δf_A$: | ||
$${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$ | $${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$ | ||
| − | Gegeben ist der Rauschabstand $10 · lg ρ_υ = 50 dB$ für Phasenmodulation und $f_N = 5 kHz$. Gesucht sind in dieser Aufgabe der Rauschabstand bei FM ($f_N = 5 kHz$) sowie die sich ergebenden Rauschabstände von PM und FM für die Nachrichtenfrequenz $f_N = | + | Gegeben ist der Rauschabstand $10 · lg ρ_υ = 50 dB$ für Phasenmodulation und $f_N = 5 kHz$. Gesucht sind in dieser Aufgabe der Rauschabstand bei FM ($f_N = 5 kHz$) sowie die sich ergebenden Rauschabstände von PM und FM für die Nachrichtenfrequenz $f_N = f_{10} = 10 kHz$. |
'''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation Kapitel 3.3]. | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [http://en.lntwww.de/Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation Kapitel 3.3]. | ||
| Line 19: | Line 19: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welcher Rauschabstand ergibt sich bei $f_N = 10 kHz$ und PM? Interpretieren Sie das Ergebnis. |
| − | |type=" | + | |type="{}"} |
| − | + | $PM, f_N = 10 kHz: 10 · lg ρ_υ$ = { 46.99 3% } $dB$ | |
| − | |||
| − | { | + | {Berechnen Sie den Rauschabstand für $f_N = 5 kHz$ und FM. Wie groß ist der Modulationsindex bei dieser Konstellation? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $FM, f_N = 5 kHz: 10 · lg ρ_υ$ = { 54.77 3% } $dB$ |
| − | |||
| + | {Berechnen Sie den Rauschabstand für $f_N = 10 kHz$ und FM. Interpretieren Sie das Ergebnis im Vergleich zu den Teilfragen a) und b). | ||
| + | |type="{}"} | ||
| + | $ FM, f_N = 10 kHz: 10 · lg ρ_υ$ = { 45.74 3% } $KHz$ | ||
</quiz> | </quiz> | ||
Revision as of 18:20, 3 January 2017
Betrachtet werden die Phasen– und Frequenzmodulation einer Cosinusschwingung mit der Frequenz $f_N$. Zunächst gelte für die Nachrichtenfrequenz $f_N = f_5 = 5 kHz$ und der Modulationsindex (Phasenhub) sei $η = 5$.
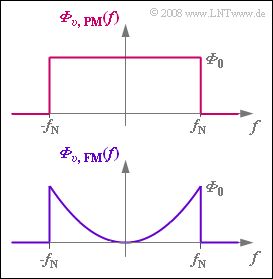
Bei Vorhandensein von additivem Gaußschen Rauschen mit der Rauschleistungsdichte N0 ergibt sich nach dem PM–Demodulator eine konstante Rauschleistungsdichte $Φ_{υ, PM}(f) = Φ_0$, die auch vom Modulationsindex abhängt: $${\it \Phi}_0 = \frac{N_0}{\eta^2} \hspace{0.05cm}.$$ Für die Berechnung der Rauschleistung $P_R$ ist lediglich der Frequenzbereich von $±f_N$ relevant (siehe Grafik).
Die Rauschleistungsdichte nach der FM–Demodulation lautet mit dem Frequenzhub $Δf_A$: $${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$ Gegeben ist der Rauschabstand $10 · lg ρ_υ = 50 dB$ für Phasenmodulation und $f_N = 5 kHz$. Gesucht sind in dieser Aufgabe der Rauschabstand bei FM ($f_N = 5 kHz$) sowie die sich ergebenden Rauschabstände von PM und FM für die Nachrichtenfrequenz $f_N = f_{10} = 10 kHz$.
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 3.3.
Fragebogen
Musterlösung