Difference between revisions of "Aufgaben:Exercise 4.4Z: Signal-to-Noise Ratio with PCM"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Pulscodemodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1619__Mod_Z_4_4.png|right|]] |
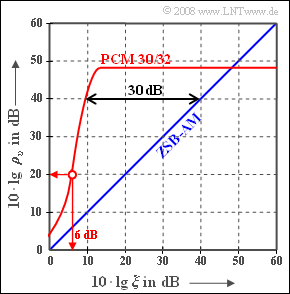
| + | Die Grafik zeigt den Sinken–Störabstand $10 · lg ρ_υ$ bei Pulscodemodulation (PCM) im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit ZSB–AM. Für letztere gilt $ρ_υ = ξ$, wobei | ||
| + | $$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} \hspace{0.05cm}.$$ | ||
| + | folgende Systemparameter zusammenfasst: | ||
| + | :* den frequenzunabhängigen Dämpfungsfaktor $α$ des Übertragungskanals, | ||
| + | :* die Leistung $P_S$ des Sendsignals $s(t)$, auch kurz Sendeleistung genannt, | ||
| + | :* die Nachrichtenfrequenz $f_N$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$, | ||
| + | :* die Rauschleistungsdichte $N_0$ des AWGN–Rauschens. | ||
| + | |||
| + | |||
| + | |||
| + | Für das PCM–System wurde auf der Seite [http://en.lntwww.de/Modulationsverfahren/Pulscodemodulation#Einfluss_von_.C3.9Cbertragungsfehlern_.284.29 Einfluss von Übertragungsfehlern (4)] folgende Näherung für das Sinken–SNR angegeben, die auch Bitfehler aufgrund des AWGN–Rauschens berücksichtigt: | ||
| + | $$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$ | ||
| + | Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und pB die Bitfehlerwahrscheinlichkeit. Da $ξ$ bei digitaler Modulation auch als die Signalenergie pro Bit bezogen auf die Rauschleistungsdichte ($E_B/N_0$) interpretiert werden kann, gilt mit dem komplementären Gaußschen Fehlersignal $Q(x)$ näherungsweise: | ||
| + | $$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$ | ||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/Pulscodemodulation Kapitel 4.1] Bei der hier betrachteten PCM handelt es sich um die PCM 30/32, deren Systemparameter zum Beispiel in der [http://en.lntwww.de/Aufgaben:4.1_PCM%E2%80%93System_30/32 Aufgabe A4.1] angegeben sind. | ||
| Line 9: | Line 24: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wieviele Bit pro Abtastwert verwendet das betrachtete PCM–System? |
| − | |type=" | + | |type="{}"} |
| − | + | $N_a$ = { 8 3% } | |
| − | |||
| − | + | {Wieviele Bit pro Abtastwert müsste man ver | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_b$= { 11 3% } |
| − | |||
| + | { | ||
</quiz> | </quiz> | ||
Revision as of 17:21, 4 January 2017
Die Grafik zeigt den Sinken–Störabstand $10 · lg ρ_υ$ bei Pulscodemodulation (PCM) im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit ZSB–AM. Für letztere gilt $ρ_υ = ξ$, wobei $$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} \hspace{0.05cm}.$$ folgende Systemparameter zusammenfasst:
- den frequenzunabhängigen Dämpfungsfaktor $α$ des Übertragungskanals,
- die Leistung $P_S$ des Sendsignals $s(t)$, auch kurz Sendeleistung genannt,
- die Nachrichtenfrequenz $f_N$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$,
- die Rauschleistungsdichte $N_0$ des AWGN–Rauschens.
Für das PCM–System wurde auf der Seite Einfluss von Übertragungsfehlern (4) folgende Näherung für das Sinken–SNR angegeben, die auch Bitfehler aufgrund des AWGN–Rauschens berücksichtigt: $$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$ Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und pB die Bitfehlerwahrscheinlichkeit. Da $ξ$ bei digitaler Modulation auch als die Signalenergie pro Bit bezogen auf die Rauschleistungsdichte ($E_B/N_0$) interpretiert werden kann, gilt mit dem komplementären Gaußschen Fehlersignal $Q(x)$ näherungsweise: $$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1 Bei der hier betrachteten PCM handelt es sich um die PCM 30/32, deren Systemparameter zum Beispiel in der Aufgabe A4.1 angegeben sind.
Fragebogen
Musterlösung