Difference between revisions of "Mobile Communications/Probability Density of Rayleigh Fading"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Zeitvariante Übertragungskanäle |Vorherige Seite=Distanzabhängige Dämpfung und Abschattung |Nächste Seite=Statistische Bindungen in…“) |
|||
| Line 74: | Line 74: | ||
Die Bildbeschreibung folgt auf der nächsten Seite.<br> | Die Bildbeschreibung folgt auf der nächsten Seite.<br> | ||
| + | |||
| + | == Modellierung von nichtfrequenzselektivem Fading (2) == | ||
| + | <br> | ||
| + | Wir betrachten die multiplikative Verfälschung <i>z</i>(<i>t</i>) entsprechend dem Rayleigh–Modell genauer. Für den komplexen Koeffizienten gilt entsprechend der letzten Seite: | ||
| + | |||
| + | :<math>z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot | ||
| + | {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} | ||
| + | \phi_{n}(t) }= | ||
| + | \sum_{n=1}^{N} \alpha_{n}(t) \cdot | ||
| + | \cos( | ||
| + | \phi_{n}( t)) + {\rm j}\cdot \sum_{n=1}^{N} \alpha_{n}(t) \cdot | ||
| + | \sin( | ||
| + | \phi_{n}( t)) | ||
| + | \hspace{0.05cm}. </math> | ||
| + | |||
| + | Das Empfangssignal <i>r</i>(<i>t</i>) ergibt sich, wenn man das Sendesignal <i>s</i>(<i>t</i>) mit der Zeitfunktion <i>z</i>(<i>t</i>) multipliziert. Es sei nochmals daran erinnert, dass sich alle Signale bzw. Zeitfunktionen <i>s</i>(<i>t</i>), <i>z</i>(<i>t</i>) und <i>r</i>(<i>t</i>) auf den äquivalenten Tiefpassbereich beziehen.<br> | ||
| + | |||
| + | [[File:P ID2109 Mob T 1 2 S2 v3.png|Rayleigh–Fading–Kanalmodell|class=fit]]<br> | ||
| + | |||
| + | Zu obiger Gleichung und der Grafik ist anzumerken: | ||
| + | *<i>α<sub>n</sub></i>(<i>t</i>) und <i>ϕ<sub>n</sub></i>(<i>t</i>) hängen von den Umgebungsbedingungen ab. <i>ϕ<sub>n</sub></i>(<i>t</i>) erfasst die verschiedenen Laufzeiten auf den <i>N</i> Pfaden und den Dopplereffekt aufgrund der Bewegung. | ||
| + | |||
| + | *Die Zeitfunktion <i>z</i>(<i>t</i>) ist eine komplexe Größe, deren Real– und Imaginärteil wir im Folgenden wieder mit <i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>) bezeichnen. | ||
| + | |||
| + | *Eine deterministische Beschreibung der Zufallsgröße <i>z</i>(<i>t</i>) = <i>x</i>(<i>t</i>) + j · <i>y</i>(<i>t</i>) ist nicht möglich, vielmehr müssen diese Funktionen durch stochastische Prozesse modelliert werden. | ||
| + | |||
| + | *Ist die Anzahl <i>N</i> der (leicht) unterschiedlichen Laufzeiten hinreichend groß, so ergeben sich nach dem zentralen Grenzwertsatz Gaußsche Zufallsgrößen <i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>). | ||
| + | |||
| + | *<i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>) sind jeweils mittelwertfrei und besitzen die gleiche Varianz <i>σ</i><sup>2</sup>: | ||
| + | |||
| + | ::<math>{\rm E}[x(t)] = {\rm E}[y(t)] = 0\hspace{0.05cm}, \hspace{0.2cm}{\rm E}[x^2(t)] = {\rm E}[y^2(t)] = \sigma^2 | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Zu berücksichtigen ist die Orthogonität von Realteil und Imaginärteil (jeweils Cosinus und Sinus des gleichen Arguments); damit sind sie auch unkorreliert. Nur bei Gaußschen Zufallsgrößen folgt daraus weiter die statistische Unabhängigkeit von <i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>). | ||
| + | |||
| + | *Aufgrund des Dopplereffekts gibt es allerdings statistische Bindungen innerhalb des Realteils <i>x</i>(<i>t</i>) und innerhalb des Imaginärteils <i>y</i>(<i>t</i>). Diese werden im Modell durch zwei Digitale Filter erzeugt. | ||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 17:24, 4 January 2017
Allgemeine Beschreibung des Mobilfunkkanals
Im Folgenden wird zur Vereinfachung der Schreibweise auf den Zusatz „TP” verzichtet. Somit liegt das reelle Signal s(t) = 1 am Eingang des Mobilfunkkanals an und das Ausgangssignal r(t) ist komplexwertig. Zusätzliche Rauschprozesse werden ausgeschlossen.
Das Funksignal s(t) kann den Empfänger über eine Vielzahl von Pfaden erreichen, wobei die einzelnen Signalanteile in unterschiedlicher Weise gedämpft und verschieden lang verzögert werden. Allgemein kann man für das Tiefpass–Empfangssignal ohne Berücksichtigung von thermischem Rauschen schreiben:
\[r(t)= \sum_{k=1}^{K} \alpha_{k}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{k}(t)} \cdot s(t - \tau_{k}) \hspace{0.05cm}.\]
Hierbei sind folgende Bezeichnungen verwendet:
- Der zeitabhängige Dämpfungsfaktor auf dem k–ten Pfad ist αk(t).
- Der zeitabhängige Phasenverlauf auf dem k–ten Pfad ist ϕk(t).
- Die Laufzeit auf dem k–ten Pfad ist τk.
Die Anzahl K der sich (zumindest geringfügig) unterscheidenden Pfade ist meist sehr groß und für eine direkte Modellierung ungeeignet. Das Modell lässt sich aber entscheidend vereinfachen, wenn man jeweils Pfade mit näherungsweise gleichen Verzögerungen zusammenfasst. Man unterscheidet somit nur noch M Hauptpfade, die durch großräumige Wegeunterschiede und damit merkliche Laufzeitunterschiede gekennzeichnet sind:
\[r(t)= \sum_{m=1}^{M} \hspace{0.1cm} \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.01cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{m,\hspace{0.02cm}n}(t)} \cdot s(t - \tau_{m,\hspace{0.02cm}n}) \hspace{0.05cm}.\]
Die beiden bisher angegebenen Gleichungen sind identisch. Eine Vereinfachung ergibt sich, wenn man für jeden Hauptpfad m die Nm Laufzeiten, die sich durch Reflexionen an Feinstrukturen sowie eventuell durch Beugungs– und Brechungserscheinungen geringfügig unterscheiden, durch eine mittlere Laufzeit ersetzt:
\[\tau_{m} = \frac{1}{N_m} \cdot \sum_{n=1}^{N_m} \tau_{m,\hspace{0.02cm}n} \hspace{0.05cm}.\]
Damit erhält man das folgende wichtige Zwischenergebnis:
\[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.01cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{m,\hspace{0.02cm}n}(t)} \hspace{0.05cm}.\]
Modellierung von nichtfrequenzselektivem Fading (1)
Ausgehend von der soeben hergeleiteten Gleichung
\[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.01cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{m,\hspace{0.02cm}n}(t)} \hspace{0.05cm}\]
können zwei wichtige Sonderfälle abgeleitet werden:
- Gibt es mehr als einen Hauptpfad (M ≥ 2), so spricht man von Mehrwegeausbreitung. Wie im Kapitel 2 noch gezeigt werden wird, kommt es dann – je nach Frequenz – zu konstruktiven oder destruktiven Überlagerungen bis hin zu völliger Auslöschung. Für manche Frequenzen erweist sich die Mehrwegeausbreitung als günstig, für andere als extrem ungünstig. Man bezeichnet diesen Effekt auch als frequenzselektives Fading.
- Bei nur einem Hauptpfad (M = 1, auf den Index „1” verzichten wir in diesem Fall) vereinfacht sich die obige Gleichung wie folgt:
- \[r(t)= z(t) \cdot s(t - \tau) \hspace{0.05cm}.\]
- Die Verzögerung τ bewirkt hier eine für alle Frequenzen konstante Laufzeit, die nicht weiter betrachtet wird. Es gibt nun keine Überlagerungen von Signalanteilen mit merklichen Laufzeitunterschieden und damit auch keine Frequenzabhängigkeit des Gesamtsignals. Man spricht deshalb von nichtfrequenzselektivem Fading oder Flat–Fading. Für dieses gilt:
- \[r(t)= z(t) \cdot s(t) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{n}(t)} \hspace{0.05cm}. \]
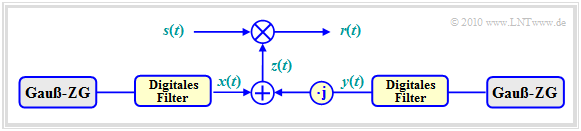
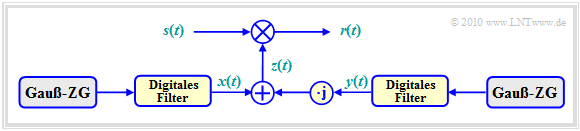
Die Grafik zeigt das Modell zur Erzeugung von nichtfrequenzselektivem Fading. Man spricht auch von Rayleigh–Fading.
Die Bildbeschreibung folgt auf der nächsten Seite.
Modellierung von nichtfrequenzselektivem Fading (2)
Wir betrachten die multiplikative Verfälschung z(t) entsprechend dem Rayleigh–Modell genauer. Für den komplexen Koeffizienten gilt entsprechend der letzten Seite:
\[z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{n}(t) }= \sum_{n=1}^{N} \alpha_{n}(t) \cdot \cos( \phi_{n}( t)) + {\rm j}\cdot \sum_{n=1}^{N} \alpha_{n}(t) \cdot \sin( \phi_{n}( t)) \hspace{0.05cm}. \]
Das Empfangssignal r(t) ergibt sich, wenn man das Sendesignal s(t) mit der Zeitfunktion z(t) multipliziert. Es sei nochmals daran erinnert, dass sich alle Signale bzw. Zeitfunktionen s(t), z(t) und r(t) auf den äquivalenten Tiefpassbereich beziehen.
Zu obiger Gleichung und der Grafik ist anzumerken:
- αn(t) und ϕn(t) hängen von den Umgebungsbedingungen ab. ϕn(t) erfasst die verschiedenen Laufzeiten auf den N Pfaden und den Dopplereffekt aufgrund der Bewegung.
- Die Zeitfunktion z(t) ist eine komplexe Größe, deren Real– und Imaginärteil wir im Folgenden wieder mit x(t) und y(t) bezeichnen.
- Eine deterministische Beschreibung der Zufallsgröße z(t) = x(t) + j · y(t) ist nicht möglich, vielmehr müssen diese Funktionen durch stochastische Prozesse modelliert werden.
- Ist die Anzahl N der (leicht) unterschiedlichen Laufzeiten hinreichend groß, so ergeben sich nach dem zentralen Grenzwertsatz Gaußsche Zufallsgrößen x(t) und y(t).
- x(t) und y(t) sind jeweils mittelwertfrei und besitzen die gleiche Varianz σ2:
- \[{\rm E}[x(t)] = {\rm E}[y(t)] = 0\hspace{0.05cm}, \hspace{0.2cm}{\rm E}[x^2(t)] = {\rm E}[y^2(t)] = \sigma^2 \hspace{0.05cm}.\]
- Zu berücksichtigen ist die Orthogonität von Realteil und Imaginärteil (jeweils Cosinus und Sinus des gleichen Arguments); damit sind sie auch unkorreliert. Nur bei Gaußschen Zufallsgrößen folgt daraus weiter die statistische Unabhängigkeit von x(t) und y(t).
- Aufgrund des Dopplereffekts gibt es allerdings statistische Bindungen innerhalb des Realteils x(t) und innerhalb des Imaginärteils y(t). Diese werden im Modell durch zwei Digitale Filter erzeugt.