Difference between revisions of "Aufgaben:Exercise 4.6: Quantization Characteristics"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Pulscodemodulation }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1623__Mod_Z_4_5.png|right|]] |
| + | Es wird die nichtlineare Quantisierung betrachtet und es gilt weiterhin das Systemmodell gemäß [http://en.lntwww.de/Aufgaben:4.5_Nichtlineare_Quantisierung Aufgabe A4.5]. Die Grafik zeigt zwei Kompressorkennlinien $q_K(q_A)$: | ||
| + | :* Rot eingezeichnet ist die sogenannte A–Kennlinie, die vom CCITT für das Standardsystem PCM 30/32 empfohlen wurde. Für $0 ≤ q_A ≤ 1$ gilt: | ||
| + | $$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\frac{1}{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < \frac{1}{A}} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | :* Der blau–gestrichelte Kurvenzug gilt für die sog. 13–Segment–Kennlinie. Diese ergibt sich aus der A–Kennlinie durch stückweise Linearisierung; sie wird in der Aufgabe A4.5 ausführlich behandelt. | ||
| + | |||
| + | Für die durchgehend rot gezeichnete A-Kennlinie ist der Quantisierungsparameter A = 100 gewählt. Mit dem vom CCITT vorgeschlagenen Wert A = 87.56 ergibt sich näherungsweise der gleiche Verlauf. Für die beiden weiteren Kurven gilt $A = A_1$ (oberer Kurvenzug) bzw. $A = A_2$ (punktierte Kurve), wobei für $A_1$ bzw. $A_2$ die beiden möglichen Zahlenwerte 50 und 200 vorgegeben sind. In der Teilaufgabe c) sollen Sie entscheiden, welche Kurve zu welchem Wert gehört. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf die [http://en.lntwww.de/Modulationsverfahren/Pulscodemodulation#Nichtlineare_Quantisierung_.281.29 letzte Theorieseite] von Kapitel 4.1. | ||
| Line 9: | Line 17: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche Argumente sprechen für die nichtlineare Quantisierung? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Das größere SNR – auch bei gleichwahrscheinlichen Amplituden. |
| − | + | + | + Bei Audio sind kleine Amplituden wahrscheinlicher als große. |
| + | + Die Verfälschung kleiner Amplituden ist subjektiv störender. | ||
| + | {Welche Unterschiede gibt es zwischen der A– und der 13–Segment–Kennlinie? | ||
| + | |type="[]"} | ||
| + | + Die A–Kennlinie beschreibt einen kontinuierlichen Verlauf. | ||
| + | + Die 13–Seg–Kurve nähert die A–Kennlinie stückweise linear an. | ||
| + | - Bei der Realisierung zeigt die A–Kennlinie wesentliche Vorteile. | ||
| − | { | + | {Lässt sich allein aus $q_A = 1 ⇒ q_K = 1$ der Parameter A ableiten? |
| + | |type="[]"} | ||
| + | - ja | ||
| + | + nein | ||
| + | |||
| + | {Lässt sich A bestimmen, wenn man vorgibt, dass der Übergang zwischen den beiden Bereichen kontinuierlich sein soll? | ||
| + | |type="[]"} | ||
| + | - ja | ||
| + | + nein | ||
| + | |||
| + | {Bestimmen Sie A aus der Bedingung $q_K(q_A = 1/2) = 0.875$. | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $q_K(q_A = 1/2) = 0.875: A$ = { 94 3% } |
| + | |||
| + | {Welche Parameterwerte werden für die weiteren Kurven verwendet? | ||
| + | |type="[]"} | ||
| + | - Es gilt $A_1 = 50$ und $A_2 = 200$. | ||
| + | + Es gilt $A_1 = 200$ und $A_2 = 50$. | ||
| + | |||
| + | |||
| Line 25: | Line 56: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die Impulsantwort $h_K(t)$ ergibt sich als das Empfangssignal r(t), wenn am Eingang ein Diracimpuls anliegt ⇒ $s(t) = δ(t)$. Daraus folgt |
| − | '''2.''' | + | $$ h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$ |
| − | '''3.''' | + | Richtig ist also der Lösungsvorschlag 1. |
| − | '''4.''' | + | |
| − | '''5.''' | + | |
| − | + | '''2.''' Der Kanalfrequenzgang $H_K(f)$ ist definitionsgemäß die Fouriertransformierte der Impulsantwort $h_K(t)$. Mit dem Verschiebungssatz ergibt sich hierfür: | |
| − | + | $$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$ | |
| + | Der erste Lösungsvorschlag ist dementsprechend falsch im Gegensatz zu den beiden anderen: $H_K(f)$ ist komplexwertig und der Betrag ist periodisch mit $1/τ$, wie die nachfolgende Rechnung zeigt: | ||
| + | $$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 =$$ | ||
| + | $$ = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$ | ||
| + | $$\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = \sqrt { 0.52 + 0.48 \cdot \cos(2 \pi f \tau) } \hspace{0.05cm}.$$ | ||
| + | Für $f = 0$ ist $|H_K(f)| = 1$. Im jeweiligen Frequenzabstand $1/τ$ wiederholt sich dieser Wert. | ||
| + | |||
| + | |||
| + | '''3.''' Wir setzen zunächst vereinbarungsgemäß K = 1. Insgesamt kommt man über vier Wege von $s(t)$ zum Ausgangssignal $b(t)$. Um die vorgegebene $h_{KR}(t)$–Gleichung zu erfüllen, muss entweder $τ_0 = 0$ gelten oder $τ_1 = 0$. Mit $τ_0 = 0$ erhält man für die Impulsantwort: | ||
| + | $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) +$$ | ||
| + | $$ + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$ | ||
| + | Um die „Hauptenergie” auf einen Zeitpunkt bündeln zu können, müsste dann $τ_1 = τ$ gewählt werden. Mit $h_0 = 0.6$ und $h_1 = 0.4$ erhält man dann $A_0 ≠ A_2$: | ||
| + | $$ h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | ||
| + | Dagegen ergibt sich mit $h_0 = 0.6$, $h_1 = 0.4$, $τ_0 = τ$ und $τ_1 = 0$: | ||
| + | $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) +$$ | ||
| + | $$ + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)=$$ | ||
| + | $$ = 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$ | ||
| + | Hier ist die Zusatzbedingung $A_0 = A_2$ erfüllt. Somit lautet das gesuchte Ergebnis: | ||
| + | $$\underline{\tau_0 = \tau = 1\,{\rm \mu s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''4.''' Für den Normierungsfaktor muss gelten: | ||
| + | $$ K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$ | ||
| + | Damit erhält man für die gemeinsame Impulsantwort (es gilt 0.24/0.52 = 6/13): | ||
| + | $$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$ | ||
| + | |||
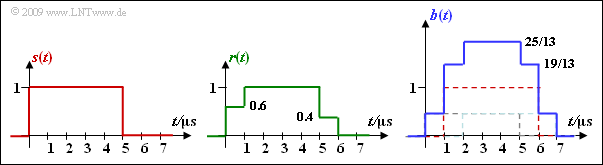
| + | '''5.''' Für das Empfangssignal $r(t)$ und für das RAKE–Ausgangssignal $b(t)$ gilt: | ||
| + | $$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm \mu s})\hspace{0.05cm},$$ | ||
| + | $$b(t) = \frac{6}{13} \cdot s(t) + 1.00 \cdot s (t - 1\,{\rm \mu s}) + \frac{6}{13} \cdot s (t - 2\,{\rm \mu s}) \hspace{0.05cm}.$$ | ||
| + | Richtig sind die Aussagen 1 und 4, wie die folgende Grafik zeigt. Die Überhöhung des Ausgangssignals ⇒ $b(t) > 1$ ist auf den Normierungsfaktor K = 25/13 zurückzuführen. Mit K = 1 wäre der Maximalwert von $b(t)$ tatsächlich 1. | ||
| + | [[File:P_ID1902__Mod_Z_5_5e.png]] | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 18:47, 4 January 2017
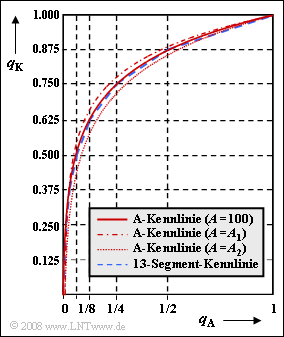
Es wird die nichtlineare Quantisierung betrachtet und es gilt weiterhin das Systemmodell gemäß Aufgabe A4.5. Die Grafik zeigt zwei Kompressorkennlinien $q_K(q_A)$:
- Rot eingezeichnet ist die sogenannte A–Kennlinie, die vom CCITT für das Standardsystem PCM 30/32 empfohlen wurde. Für $0 ≤ q_A ≤ 1$ gilt:
$$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\frac{1}{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < \frac{1}{A}} \hspace{0.05cm}. \\ \end{array}$$
- Der blau–gestrichelte Kurvenzug gilt für die sog. 13–Segment–Kennlinie. Diese ergibt sich aus der A–Kennlinie durch stückweise Linearisierung; sie wird in der Aufgabe A4.5 ausführlich behandelt.
Für die durchgehend rot gezeichnete A-Kennlinie ist der Quantisierungsparameter A = 100 gewählt. Mit dem vom CCITT vorgeschlagenen Wert A = 87.56 ergibt sich näherungsweise der gleiche Verlauf. Für die beiden weiteren Kurven gilt $A = A_1$ (oberer Kurvenzug) bzw. $A = A_2$ (punktierte Kurve), wobei für $A_1$ bzw. $A_2$ die beiden möglichen Zahlenwerte 50 und 200 vorgegeben sind. In der Teilaufgabe c) sollen Sie entscheiden, welche Kurve zu welchem Wert gehört.
Hinweis: Die Aufgabe bezieht sich auf die letzte Theorieseite von Kapitel 4.1.
Fragebogen
Musterlösung
2. Der Kanalfrequenzgang $H_K(f)$ ist definitionsgemäß die Fouriertransformierte der Impulsantwort $h_K(t)$. Mit dem Verschiebungssatz ergibt sich hierfür:
$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$
Der erste Lösungsvorschlag ist dementsprechend falsch im Gegensatz zu den beiden anderen: $H_K(f)$ ist komplexwertig und der Betrag ist periodisch mit $1/τ$, wie die nachfolgende Rechnung zeigt:
$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 =$$
$$ = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$
$$\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = \sqrt { 0.52 + 0.48 \cdot \cos(2 \pi f \tau) } \hspace{0.05cm}.$$
Für $f = 0$ ist $|H_K(f)| = 1$. Im jeweiligen Frequenzabstand $1/τ$ wiederholt sich dieser Wert.
3. Wir setzen zunächst vereinbarungsgemäß K = 1. Insgesamt kommt man über vier Wege von $s(t)$ zum Ausgangssignal $b(t)$. Um die vorgegebene $h_{KR}(t)$–Gleichung zu erfüllen, muss entweder $τ_0 = 0$ gelten oder $τ_1 = 0$. Mit $τ_0 = 0$ erhält man für die Impulsantwort:
$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) +$$
$$ + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$
Um die „Hauptenergie” auf einen Zeitpunkt bündeln zu können, müsste dann $τ_1 = τ$ gewählt werden. Mit $h_0 = 0.6$ und $h_1 = 0.4$ erhält man dann $A_0 ≠ A_2$:
$$ h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
Dagegen ergibt sich mit $h_0 = 0.6$, $h_1 = 0.4$, $τ_0 = τ$ und $τ_1 = 0$:
$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) +$$
$$ + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)=$$
$$ = 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$
Hier ist die Zusatzbedingung $A_0 = A_2$ erfüllt. Somit lautet das gesuchte Ergebnis:
$$\underline{\tau_0 = \tau = 1\,{\rm \mu s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$
4. Für den Normierungsfaktor muss gelten: $$ K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$ Damit erhält man für die gemeinsame Impulsantwort (es gilt 0.24/0.52 = 6/13): $$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
5. Für das Empfangssignal $r(t)$ und für das RAKE–Ausgangssignal $b(t)$ gilt:
$$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm \mu s})\hspace{0.05cm},$$
$$b(t) = \frac{6}{13} \cdot s(t) + 1.00 \cdot s (t - 1\,{\rm \mu s}) + \frac{6}{13} \cdot s (t - 2\,{\rm \mu s}) \hspace{0.05cm}.$$
Richtig sind die Aussagen 1 und 4, wie die folgende Grafik zeigt. Die Überhöhung des Ausgangssignals ⇒ $b(t) > 1$ ist auf den Normierungsfaktor K = 25/13 zurückzuführen. Mit K = 1 wäre der Maximalwert von $b(t)$ tatsächlich 1.