Difference between revisions of "Aufgaben:Exercise 5.2: Band Spreading and Narrowband Interferer"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1868__Mod_A_5_2.png|right|]] |
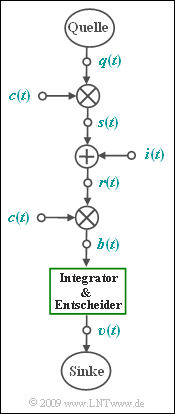
| + | Betrachtet wird ein Spread Spectrum System gemäß der vorliegenden Grafik im äquivalenten Tiefpassbereich. Das Digitalsignal $q(t)$ besitze das Leistungsdichtespektrum $Φ_q(f)$, das als rechteckförmig mit der Bandbreite $B = 1/T = 100 kHz$ angenähert werden soll: | ||
| + | $${\it \Phi}_{q}(f) = | ||
| + | \left\{ \begin{array}{c} {\it \Phi}_{q0} \\ | ||
| + | 0 \\ \end{array} \right. | ||
| + | \begin{array}{*{10}c} {\rm{f\ddot{u}r}} | ||
| + | \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} | ||
| + | |f| <B/2 \hspace{0.05cm}, \\ | ||
| + | \\ | ||
| + | \end{array}$$ | ||
| + | Im Tiefpassbereich ist somit die Bandbreite (nur die Anteile bei positiven Frequenzen) gleich B/2. Die Bandbreite im Bandpassbereich ist B. | ||
| + | Die Bandspreizung erfolgt durch Multiplikation mit der PN–Sequenz $c(t)$ der Chipdauer $T_c = T/100$ (PN steht dabei für Pseudo Noise). Für die Autokorrelationsfunktion gelte vereinfachend: | ||
| + | $$ {\it \varphi}_{c}(\tau) = \left\{ \begin{array}{c}1 - |\tau|/T_c \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} -T_c \le \tau \le T_c \hspace{0.05cm}, \\ \\ \end{array}$$ | ||
| + | Beim Empfänger wird wieder die gleiche Spreizfolge c(t) phasensynchron zugesetzt. | ||
| + | |||
| + | Das Interferenzsignal $i(t)$ soll zunächst vernachlässigt werden. In der Teilaufgabe (d) bezeichnet $i(t)$ einen schmalbandigen Störer bei der Trägerfrequenz $f_T = 30 MHz = f_I$ mit der Leistung $P_I$. Der Einfluss des AWGN–Rauschens $n(t)$ wird in dieser Aufgabe nicht betrachtet. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/PN%E2%80%93Modulation Kapitel 5.2]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie lautet das Leistungsdichtespektrum des Spreizsignals $c(t)$? Welcher Wert ergibt sich bei der Frequenz f = 0? |
| − | |type=" | + | |type="{}"} |
| − | - | + | $Φ_c(f = 0)$ = { 1 3% } $10^-7$ $1/Hz$ |
| − | |||
| − | |||
| − | { | + | {Berechnen Sie die äquivalente Bandbreite $B_c$ des Spreizsignals als Breite des flächengleichen LDS–Rechtecks: |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $B_C$ = { 10 3% } $MHz$ |
| − | |||
| + | {Welche Aussagen sind für die Bandbreiten der Signale $s(t)$ und $b(t)$ zutreffend? Die (zweiseitige) Bandbreite von $q(t)$ ist B. | ||
| + | |type="[]"} | ||
| + | - $B_s$ ist exakt gleich $B_c$. | ||
| + | + $B_s$ ist näherungsweise gleich $B_c + B$. | ||
| + | - $B_b$ ist exakt gleich $B_s$. | ||
| + | - $B_b$ ist gleich $B_s + B_c = 2B_c + B$. | ||
| + | + $B_b$ ist exakt gleich B. | ||
| + | {Welchen Einfluss hat eine Bandspreizung auf einen schmalbandigen Störer bei der Trägerfrequenz? Es gelte also $f_I = f_T$. | ||
| + | |type="[]"} | ||
| + | + Der störende Einfluss wird durch Bandspreizung abgeschwächt. | ||
| + | - Die Störleistung ist nur mehr halb so groß. | ||
| + | - Die Störleistung wird durch die Bandspreizung nicht verändert. | ||
</quiz> | </quiz> | ||
Revision as of 18:38, 6 January 2017
Betrachtet wird ein Spread Spectrum System gemäß der vorliegenden Grafik im äquivalenten Tiefpassbereich. Das Digitalsignal $q(t)$ besitze das Leistungsdichtespektrum $Φ_q(f)$, das als rechteckförmig mit der Bandbreite $B = 1/T = 100 kHz$ angenähert werden soll: $${\it \Phi}_{q}(f) = \left\{ \begin{array}{c} {\it \Phi}_{q0} \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} |f| <B/2 \hspace{0.05cm}, \\ \\ \end{array}$$ Im Tiefpassbereich ist somit die Bandbreite (nur die Anteile bei positiven Frequenzen) gleich B/2. Die Bandbreite im Bandpassbereich ist B.
Die Bandspreizung erfolgt durch Multiplikation mit der PN–Sequenz $c(t)$ der Chipdauer $T_c = T/100$ (PN steht dabei für Pseudo Noise). Für die Autokorrelationsfunktion gelte vereinfachend: $$ {\it \varphi}_{c}(\tau) = \left\{ \begin{array}{c}1 - |\tau|/T_c \\ 0 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{sonst}} \hspace{0.05cm}. \\ \end{array}\begin{array}{*{20}c} -T_c \le \tau \le T_c \hspace{0.05cm}, \\ \\ \end{array}$$ Beim Empfänger wird wieder die gleiche Spreizfolge c(t) phasensynchron zugesetzt.
Das Interferenzsignal $i(t)$ soll zunächst vernachlässigt werden. In der Teilaufgabe (d) bezeichnet $i(t)$ einen schmalbandigen Störer bei der Trägerfrequenz $f_T = 30 MHz = f_I$ mit der Leistung $P_I$. Der Einfluss des AWGN–Rauschens $n(t)$ wird in dieser Aufgabe nicht betrachtet.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 5.2.
Fragebogen
Musterlösung