Soft-in Soft-Out Decoder

1. Channel Coding
2. Iterative Decodierverfahren
3. Soft-in Soft-Out Decoder

• Previous page
• Next page

• Previous page
• Next page

Hard Decision vs. Soft Decision (1)

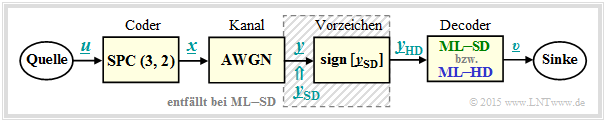
Zur Hinleitung auf die Thematik dieses vierten und letzten Kapitels und zur Motivation betrachten wir das folgende Nachrichtenübertragungssystem mit Codierung.

Nachfolgend werden alle Symbole in bipolarer Darstellung angegeben: „0”  →  „+1” und „1”  →  „–1”.

• Die Symbolfolge u = (u₁, u₂) wird der Coderfolge x = (x₁, x₂, x₃) = (u₁, u₂, p) zugeordnet, wobei für das Paritybit p = u₁ ⊕ u₂ gilt  ⇒  Single Parity–check Code  ⇒  SPC (3, 2, 2).
  

• Der AWGN–Kanal verändert die Binärsymbole x_i ∈ {+1, –1} zu reellwertigen Ausgangswerten y_i, z.B. im Block 4 der unteren Tabelle:   x₁ = +1  ⇒  y₁ = +0.9  und   x₃ = –1  ⇒  y₃ = +0.1.
  

• Die Decodierung geschieht gemäß dem Kriterium Maximum Likelihood (block–wise ML), wobei zwischen Hard Decision (ML–HD) und Soft Decision (ML–SD) zu unterscheiden ist.
  

• Das obige Blockschaltbild in seiner Gesamtheit entspricht ML–HD. Hier werden zur Detektion nur die Vorzeichen der AWGN–Ausgangswerte entsprechend  y_{HD, i} = sign[y_{SD, i}]  ausgewertet.
  

• Bei Soft Decision (ML–SD) verzichtet man auf den schraffierten Block in obigem Blockschaltbild und wertet direkt die wertkontinuierlichen Eingangsgrößen y_{SD, i} aus.
  

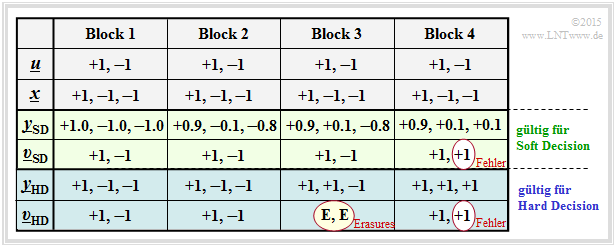
Aus der Beispieltabelle erkennt man:

• Hard Decision  ⇒ die Symbolfolge υ_HD ergibt sich aus den hart entschiedenen Kanalwerten y_HD (blaue Hinterlegung): Es werden nur die beiden ersten Blöcke fehlerfrei decodiert.
  

• Soft Decision  ⇒ die Symbolfolge υ_SD ergibt sich aus den „weichen” Kanalausgangswerten y_SD (grüne Hinterlegung): Nun wird in diesem Beispiel auch der dritte Block richtig entschieden.
  
  

Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.

Hard Decision vs. Soft Decision (2)

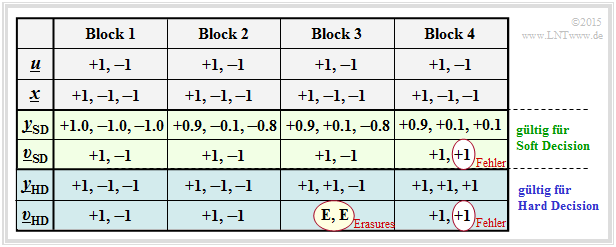
Für alle Spalten der folgenden Tabelle wird vorausgesetzt:

• der Nachrichtenblock u = (0, 1), bipolar darstellbar als (+1, –1),
  

• der SPC (3, 2)–codierte Block x = (0, 1, 1) bzw. in Bipolardarstellung (+1, –1, –1).
  
  

Die vier Blöcke unterscheiden sich also nur durch unterschiedliche AWGN–Realisierungen.

Die Tabelle ist wie folgt zu interpretieren:

• Bei idealem Kanal entsprechend Block 1  ⇒  x = y_SD = y_HD gibt es keinen Unterschied zwischen der (blauen) herkömmlichen ML–HD –Variante und der (grünen) ML–SD –Variante.
  

• Der Block 2 demonstriert geringe Signalverfälschungen. Wegen y_HD = x (das heißt, dass der Kanal die Vorzeichen nicht verfälscht) liefert auch ML–HD das richtige Ergebnis υ_HD = u.
  

• Dagegen gilt im dritten Block y_HD ≠ x und es gibt auch keine SPC (3, 2)–Zuordnung u  ⇒  y_HD. Der ML–Decoder kann hier nur durch die Ausgabe υ_HD = (E, E) vermelden, dass er bei der Decodierung dieses Blocks gescheitert ist. „E” steht hierbei für Erasure (deutsch: Auslöschung).
  

• Auch der Soft Decision Decoder erkennt, dass eine Decodierung anhand der Vorzeichen nicht funktioniert. Anhand der y_SD–Werte erkennt er aber, dass mit großer Wahrscheinlichkeit das zweite Bit verfälscht wurde und entscheidet sich für die richtige Symbolfolge υ_SD = (+1, –1) = u.
  

• Im vierten Block werden durch den AWGN–Kanal sowohl die Vorzeichen von Bit 2 als auch von Bit 3 verändert, was zum Ergebnis υ_HD = (+1, +1) ≠ u (+1, –1) führt  ⇒  ein Blockfehler und gleichzeitig ein Bitfehler. Auch der Soft Decision Decoder liefert hier das gleiche falsche Ergebnis.
  
  

Die Decodiervariante ML–SD bietet gegenüber ML–HD zudem den Vorteil, dass man relativ einfach jedes Decodierergebnis mit einem Zuverlässigkeitswert versehen kann (in obiger Tabelle ist dieser allerdings nicht angegeben). Dieser Zuverlässigkeitswert

• hätte bei Block 1 seinen Maximalwert,
  

• wäre bei Block 2 deutlich kleiner,
  

• läge bei Block 3 und 4 nahe bei 0.
  

Zuverlässigkeitsinformation – Log Likelihood Ratio (1)

Es sei x ∈ {+1, –1} eine binäre Zufallsvariable mit den Wahrscheinlichkeiten Pr(x = +1) und Pr(x = –1). Für die Codierungstheorie erweist es sich als zweckmäßig hinsichtlich der Rechenzeiten, wenn man anstelle der Wahrscheinlichkeiten Pr(x = ±1) den natürlichen Logarithmus des Quotienten heranzieht.

: Das Log–Likelihood–Verhältnis (kurz: der L–Wert, englisch: Log–Likelihood Ratio, LLR) der Zufallsgröße x ∈ {+1, –1} lautet:

\[L(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = +1)}{{\rm Pr}(x = -1)}\hspace{0.05cm}.\]

Bei unipolarer/symbolhafter Darstellung (+1 → 0  und  –1 → 1) gilt entsprechend mit ξ ∈ {0, 1}:

\[L(\xi)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(\xi = 0)}{{\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]

Nachfolgend ist der nichtlineare Zusammenhang zwischen Pr(x = ±1) und L(x) angegeben. Ersetzt man Pr(x = +1) durch Pr(ξ = 0), so gibt die mittlere Zeile den L–Wert der unipolaren Zufallsgröße ξ an.

Man erkennt:

• Der wahrscheinlichere Zufallswert von x ∈ {+1, –1} ist durch sign L(x)  ⇒  Vorzeichen gegeben.
  

• Dagegen gibt der Betrag |L(x)| die Zuverlässigkeit für das Ergebnis sign(L(x)) an.
  
  

:

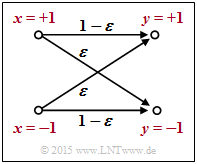Wir betrachten das skizzierte BSC–Modell mit bipolarer Darstellung. Hier gilt mit der Verfälschungswahrscheinlichkeit ε = 0.1 sowie den beiden Zufallsgrößen x ∈ {+1, –1} und y ∈ {+1, –1} am Eingang und Ausgang des Kanals:

\[L(y\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.15cm} = \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = +1)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = -1)} = \] \[\hspace{-0.15cm} = \hspace{-0.15cm} \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]

Beispielsweise ergeben sich für ε = 0.1 folgende Zahlenwerte (vergleiche obere Tabelle):

\[L(y = +1\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.2cm} L(y = -1\hspace{0.05cm}|\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]

Dieses Beispiel zeigt, dass man die sog. L–Wert–Algebra auch auf bedingte Wahrscheinlichkeiten anwenden kann. In Aufgabe Z4.1 wird das BEC–Modell in ähnlicher Weise beschrieben.

Zuverlässigkeitsinformation – Log Likelihood Ratio (2)

Wir betrachten nun den AWGN–Kanal mit den beiden bedingten Wahrscheinlichkeitsdichtefunktionen

\[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\] \[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]

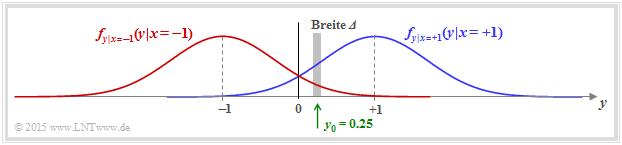
In der Grafik sind zwei beispielhafte Gaußfunktionen als blaue bzw. rote Kurve dargestellt.

Die gesamte WDF des Ausgangssignals y ergibt sich aus der (gleich) gewichteten Summe:

\[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}| \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]

Berechnen wir nun die Wahrscheinlichkeit, dass der Empfangswert y in einem (sehr) schmalen Intervall der Breite Δ um y₀ = 0.25 liegt, so erhält man näherungsweise

\[{\rm Pr} (|y - y_0| \le{\it \Delta}/2 \hspace{0.05cm} \Big | \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\] \[{\rm Pr} (|y - y_0| \le {\it \Delta}/2 \hspace{0.05cm} \Big | \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]

Die etwas größeren senkrechten Striche bezeichnen die Bedingungen, die kleineren die Betragsbildung.

Der L–Wert der bedingten Wahrscheinlichkeit in Vorwärtsrichtung (das bedeutet: Ausgang y für einen gegebenen Eingang x) ergibt sich somit als der Logarithmus des Quotienten beider Ausdrücke:

\[L(y = y_0\hspace{0.05cm}|\hspace{0.05cm}x) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ]\hspace{0.15cm} = \] \[\hspace{2.4cm} = \hspace{-0.1cm} \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]

Ersetzen wir nun die Hilfsgröße y₀ durch die (allgemeine) Zufallsgröße y am AWGN–Ausgang, so lautet das Endergebnis:

\[L(y \hspace{0.05cm}|\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]

Hierbei ist K_L = 2/σ² eine Konstante, die allein von der Streuung der Gaußschen Störung abhängt.

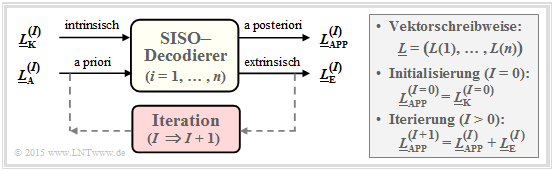
Symbolweise Soft–in Soft–out Decodierung

Wir gehen nun von einem (n, k)–Blockcode aus, wobei das Codewort x = (x₁, ... , x_n) durch den Kanal in das Empfangswort y = (y₁, ... , y_n) verfälscht wird. Bei langen Codes ist eine Maximum–a–posteriori–Entscheidung auf Blockebene – kurz: block–wise MAP – sehr aufwändig. Man müsste unter den 2^k zulässigen Codeworten x_j ∈ C dasjenige mit der größten Rückschlusswahrscheinlichkeit (englisch: A Posteriori Probability, APP) finden. Das auszugebende Codewort z wäre in diesem Fall

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]

Eine zweite Möglichkeit ist die Decodierung auf Bitebene. Der dargestellte symbolweise (oder bitweise) Soft–in Soft–out Decoder hat die Aufgabe, alle Codewortbits x_i ∈ {0, 1} entsprechend maximaler Rückschlusswahrscheinlichkeit Pr(x_i | y) zu decodieren. Mit der Laufvariablen i = 1, ... , n gilt dabei:

• Der entsprechende L–Wert (englisch: Log Likelihood Ratio, LLR) für das i–te Codebit lautet:

\[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]

• Der Decoder arbeitet iterativ. Bei der Initialisierung (gekennzeichnet durch den Parameter I = 0) ist L_APP(i) = L_K(i), wobei das Kanal–LLR L_K(i) durch den Empfangswert y_i gegeben ist.
  

• Berechnet wird zudem der extrinsische L–Wert L_E(i), der die gesamte Information quantifiziert, die alle anderen Bits (j ≠ i) aufgrund der Code–Eigenschaften über das betrachtete i–te Bit liefern.
  

• Bei der nächsten Iteration (ab I = 1) wird L_E(i) bei der Berechnung von L_APP(i) als Apriori–Information L_A(i) berücksichtigt. Für das neue Aposteriori–LLR in der Iteration I + 1 gilt somit:

\[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]

• Die Iterationen werden fortgesetzt, bis alle |L_APP(i)| größer sind als ein vorzugebender Wert. Das wahrscheinlichste Codewort z ergibt sich dann aus den Vorzeichen aller L_APP(i), mit i = 1, ... , n.
  

• Bei einem systematischen Code geben die ersten k Bit von z das gesuchte Informationswort an, das mit großer Wahrscheinlichkeit mit der gesendeten Nachricht u übereinstimmen wird.
  
  

Diese Beschreibung des SISO–Decodierers nach [Bos98] soll in erster Linie die unterschiedlichen L–Werte verdeutlichen. Das große Potential der symbolweisen Decodierung erkennt man allerdings erst im Zusammenhang mit verketteten Codiersystemen.

Zur Berechnung der extrinsischen L–Werte (1)

Die Schwierigkeit bei der symbolweisen iterativen Decodierung ist im allgemeinen die Bereitstellung der extrinsischen L–Werte L_E(i). Bei einem Code der Länge n gilt hierbei für die Laufvariable: i = 1, ... , n.

: Der extrinsische L–Wert (englisch: extrinsic LLR) ist ein Maß für die Informationen, den die anderen Symbole (j ≠ i) des Codewortes über das i–te Codesymbol liefern, ausgedrückt als Log–Likelihood–Verhältnis. Wir benennen diesen Kennwert mit L_E(i).

Wir berechnen nun die extrinsischen L–Werte L_E(i) für zwei beispielhafte Codes.

Repetition Code ⇒ RC (n, 1, n)

Ein Wiederholungscode zeichnet sich dadurch aus, dass alle n Codesymbole x_i ∈ {0, 1} identisch sind. Der extrinsische L–Wert für das i–ten Symbol ist hier sehr einfach anzugeben und lautet:

\[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]

Ist die Summe über alle L_j≠i positiv, so bedeutet dies aus Sicht der anderen L–Werte eine Präferenz für „x_i = 0”. Bei negativer Summe ist „x_i = 1” wahrscheinlicher. L_E(i) = 0 erlaubt keine Vorhersage.

: Wir betrachten die Decodierung eines Wiederholungscodes (n = 4), wobei gelten soll:

• L = (+1, –1, +3, –1)  ⇒  L_E = (+1, +3, –1, +3): L_E(1) ist positiv, obwohl zwei der anderen

L–Werte (Mehrheit) negativ sind  ⇒  Präferenz für „x₁ = 0”. Alle Aposteriori–L–Werte sind nach einer Iteration positiv  ⇒  Informationsbit ist u = 0. Weitere Iterationen bringen nichts.

• L = (+1, +1, –4, +1)  ⇒  L_E = (–2, –2, +3, –2): Alle Aposteriori–L–Werte sind

nach zwei Iterationen negativ  ⇒  Informationsbit ist u = 1  ⇒  zu Beginn waren drei Vorzeichen falsch.

• L = (+1, +1, –3, +1)  ⇒  L_E = (–1, –1, +3, –1): Alle Aposteriori–L–Werte sind

nach einer Iteration 0  ⇒  Informationsbit kann nicht decodiert werden. Weitere Iterationen bringen nichts.

Zur Berechnung der extrinsischen L–Werte (2)

Single Parity–check Code ⇒ SPC (n, n –1, 2)

Bei jedem Single Parity–check Code ist die Anzahl der Einsen in jedem Codewort geradzahlig. Oder anders ausgedrückt: Für jedes Codewort x ist das Hamming–Gewicht w_H(x) geradzahlig.

Das Codewort x^(–i) beinhalte alle Symbole mit Ausnahme von x_i  ⇒  Vektor der Länge n – 1. Damit lautet der extrinsische L–Wert bezüglich dieses i–ten Symbols, wenn x empfangen wurde:

\[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]

Wie in der Aufgabe A4.4 gezeigt werden soll, kann hierfür auch geschrieben werden:

\[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]

: Wir gehen vom Single Parity–check Code mit n = 3, k = 2  ⇒  kurz SPC (3, 2, 2) aus. Die <nobr>2^k = 4</nobr> gültigen Codeworte x = {x₁, x₂, x₃} lauten bei bipolarer Beschreibung  ⇒  x_i ∈ {±1}:

\[ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, \hspace{0.3cm} \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, \hspace{0.3cm} \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, \hspace{0.3cm} \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. \]

Bei diesem Code ist also das Produkt x₁ · x₂ · x₃ stets positiv.

Die Tabelle zeigt den Decodiervorgang für L_APP = (+2.0, +0.4, –1.6). Die harte Entscheidung nach den Vorzeichen von L_APP(i) ergäbe hier (+1, +1, –1), also kein gültiges Codewort des SP(3, 2, 2).

Rechts sind in der Tabelle die dazugehörigen extrinsischen L–Werte eingetragen:

\[L_{\rm E}(1) \hspace{-0.15cm} = \hspace{-0.15cm} 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \] \[L_{\rm E}(2) \hspace{-0.15cm} = \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \] \[L_{\rm E}(3) \hspace{-0.15cm} = \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]

Die zweite Gleichung lässt sich wie folgt interpretieren:

• L_APP(1) = +2.0 und L_APP(3) = –1.6 sagen aus, dass Bit 1 eher „+1” als „–1” ist und Bit 3 eher „–1” als „+1”. Die Zuverlässigkeit (Betrag) ist beim ersten Bit etwas größer als beim dritten.
  

• Die extrinsische Information L_E(2) = –0.518 berücksichtigt nur die Informationen von Bit 1 und Bit 3 über Bit 2. Aus deren Sicht ist das zweite Bit eine „–1” mit der Zuverlässigkeit 0.518.
  

• Der vom Empfangswert y₂ abgeleitete L–Wert  ⇒  L_APP(2) = +0.4 hat für das zweite Bit eine „+1” vermuten lassen. Die Diskrepanz wird hier bereits in der Iteration I = 1 aufgelöst.
  

• Entschieden wird hier für das Codewort x₁. Bei 0.518 < L_APP(2) < 1.6 würde das Ergebnis x₁ erst nach mehreren Iterationen vorliegen. Für L_APP(2) > 1.6 liefert der Decoder dagegen x₀.