Binomial Distribution

Allgemeine Beschreibung der Binomialverteilung

Die Binomialverteilung stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar.

Zur Herleitung der Binomialverteilung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i$

den Wert $1$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 1) = p$, und
den Wert $0$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 0) = 1-p$ annehmen kann.

Dann ist die Summe $z$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat $\{0, 1, 2, ... , I\}$, die man als binomialverteilt bezeichnet:

$$z=\sum_{i=1}^{I}b_i.$$

Der Symbolumfang beträgt somit $M = I + 1.$

Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen:

Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle.
Sie erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung.
Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße.

Wahrscheinlichkeiten der Binomialverteilung

Für die Wahrscheinlichkeiten der Binomialverteilung gilt mit $μ = 0, ... , I$: $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ Der erste Term gibt hierbei die Anzahl der Kombinationen („$I$ über $μ$”) an: $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$

Weitere Hinweise:

Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene Poissonverteilung angenähert werden.
Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.

rechts

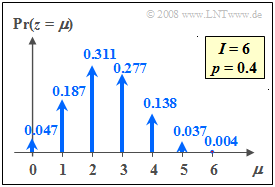
Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung sind für $I =6$ und $p =0.4$. Von Null verschieden sind somit $M = I+1=7$ Wahrscheinlichkeiten.

Dagegen ergeben sich für $I = 6$ und $p = 0.5$ die folgenden Binomialwahrscheinlichkeiten: $$\begin{align*}{\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}0) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}6)\hspace{-0.05cm} =\hspace{-0.05cm} 1/64\hspace{-0.05cm} = \hspace{-0.05cm}0.015625 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}1) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}5) \hspace{-0.05cm}= \hspace{-0.05cm}6/64 \hspace{-0.05cm}=\hspace{-0.05cm} 0.09375,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}2) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}4)\hspace{-0.05cm} = \hspace{-0.05cm}15/64 \hspace{-0.05cm}= \hspace{-0.05cm}0.234375 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}3) & = 20/64 \hspace{-0.05cm}= \hspace{-0.05cm} 0.3125 .\end{align*}$$

Diese sind symmetrisch bezüglich des Abszissenwertes $\mu = I/2$.

Mit nachfolgendem Berechnungsmodul können Sie die Binomialwahrscheinlichkeiten auch für andere Parameterwerte $I$ und $p$ ermitteln:

Ereigniswahrscheinlichkeiten der Binomialverteilung

Blockfehlerwahrscheinlichkeit

Ein weiteres Beispiel für die Anwendung der Binomialverteilung ist die Berechnung der Blockfehlerwahrscheinlichkeit bei einem digitalen Übertragungssystem.

Überträgt man jeweils Blöcke von $I =10$ Binärsymbolen über einen Kanal, der

mit der Wahrscheinlichkeit $p = 0.01$ ein Symbol verfälscht ⇒ Zufallsgröße $e_i = 1$, und
entsprechend mit der Wahrscheinlichkeit $1 – p = 0.99$ das Symbol unverfälscht überträgt ⇒ Zufallsgröße $e_i = 0$,

so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”): $$f=\sum_{i=1}^{I}e_i.$$

Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $0$ (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ$.

Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1.
Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf:

$$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$

Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = $10$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =1$ gelten soll.

Für $f =2$ gibt es deutlich mehr Kombinationen, nämlich „10 über 2“ = $45$, und man erhält

$$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$

Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $$p_{\rm R} = \it p_{\rm 3} \rm +... \rm + \it p_{\rm 10}\approx \rm 10^{-4},$$ oder $$p_{\rm R} = \rm 1-\it p_{\rm 0}-\it p_{\rm 1}-p_{\rm 2}\approx \rm 10^{-4}.$$

Man erkennt, dass die zweite Berechnungsmöglichkeit über das Komplement schneller zum Ziel führt. Man könnte aber auch berücksichtigen, dass bei diesen Zahlenwerten $p_{\rm R} ≈ p_3$ gilt.

Momente der Binomialverteilung

Die Momente können mit den Gleichungen im Kapitel Momente einer diskreten Zufallsgröße und den Wahrscheinlichkeiten der Binomialverteilung allgemein berechnet werden.

Für das Moment $k$-ter Ordnung einer binomialverteilten Zufallsgröße gilt: $$m_k=\rm E[\it z^k \rm ]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$

Daraus erhält man nach einigen Umformungen für

den linearen Mittelwert:

$$m_1 = I\cdot p,$$

den quadratischen Mittelwert:

$$m_2 = (I^2-I)\cdot p^2+I\cdot p.$$

Die Varianz und die Streuung erhält man durch Anwendung des „Steinerschen Satzes”:

$$\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$$

Die maximale Varianz $σ^2 = I/4$ ergibt sich für die charakteristische Wahrscheinlichkeit $p = 1/2$. In diesem Fall sind die Wahrscheinlichkeit symmetrisch um den Mittelwert $m_1 = I/2 \ ⇒ \ p_μ = p_{I–μ}$.

Je mehr die charakteristische Wahrscheinlichkeit $p$ vom Wert $1/2$ abweicht,

um so kleiner ist die Streuung $σ$, und
um so unsymmetrischer werden die Wahrscheinlichkeiten um den Mittelwert $m_1 = I · p$.

Wir betrachten wie im letzten Beispiel einen Block von $I =10$ Binärsymbolen, die jeweils mit der Wahrscheinlichkeit $p = 0.01$ unabhängig voneinander verfälscht werden. Dann gilt:

Die mittlere Anzahl von Fehlern pro Block ist gleich $m_f = {\rm E}[ f] = I · p = 0.1$.
Die Streuung (Standardabweichung) der Zufallsgröße $f$ beträgt $σ_f = \sqrt{0.1 \cdot 0.99}≈ 0.315$.

Im vollständig gestörten Kanal ⇒ Verfälschungswahrscheinlichkeit $p = 1/2$ ergeben sich demgegenüber die Werte

$m_f = 5$ ⇒ im Mittel sind fünf der zehn Bits innerhalb eines Blocks falsch,
$σ_f = \sqrt{I}/2 ≈1.581$ ⇒ maximale Streuung für $I = 10$.

Aufgaben zum Kapitel

Aufgabe 2.3: Summe von Binärzahlen

Aufgabe 2.4: Zahlenlotto (6 aus 49)