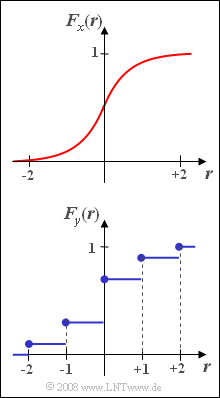
Exercise 3.2: CDF for Exercise 3.1
From LNTwww
Es gelten die gleichen Voraussetzungen wie bei Aufgabe 3.1.
- Die WDF der wertkontinuierlichen Zufallsgröße ist in den Bereichen $|x| > 2$ identisch Null, und im Bereich $-2 \le x \le +2$ gilt:
- $$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$
- Auch die diskrete Zufallsgröße $y$ ist auf den Bereich $\pm 2$ begrenzt. Es gelten folgende Wahrscheinlichkeiten:
- $${\rm \Pr}(y=0)=0.4,$$
- $${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$
- $${\rm \Pr}(y=+2)={\rm \Pr}(y=-2)=0.1.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichtefunktion.
- Eine Zusammenfassung der hier behandelten Thematik bietet das Lernvideo Zusammenhang zwischen WDF und VTF.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Gegeben ist die folgende Gleichung:
- $$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$
Fragebogen
Musterlösung
- 1. Da x eine kontinuierliche Zufallsgröße und auf den Bereich |x| < 2 begrenzt ist, sind alle drei vorgegebenen Aussagen richtig.
- 2. Bei einer diskreten Zufallsgröße steigt die Verteilungsfunktion nur schwach monoton an, d. h. es gibt außer Sprüngen ausschließlich horizontale Abschnitte der VTF. Da an den Sprungstellen jeweils der rechtsseitige Grenzwert gilt, ist demzufolge Fy(–2) = 0.1, also ungleich 0. Richtig sind somit die Aussagen 2 und 3.
- 3. Die VTF Fx(r) berechnet sich als das Integral von –∞ bis r über die WDF fx(x). Aufgrund der Symmetrie kann hierfür im Bereich 0 ≤ r ≤ 2 geschrieben werden:
- $$\it F_{\it x} (\it r) =\rm \frac{1}{2} + \rm \int\limits_{0}^{\it r} \it f_x(x)\;{\rm d}x = \rm \frac{1}{2} + \int\limits_{0}^{\it r}\rm \frac{1}{2}\cdot cos^2 (\frac{\pi}{4}\cdot \it x)\;{\rm d}x.$$
- In gleicher Weise wie bei Aufgabe A3.1(g) erhält man somit:
- $$\it F_{\it x} (\it r) =\rm \frac{1}{2} + \frac{\it r}{\rm 4} + \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2}\cdot \it r),$$
- $$\it F_{\it x} (\it r= \rm 0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$
- $$\it F_{\it x}(\it r=\rm 1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$
- $$\it F_{\it x}(\it r=\rm 2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$
- 4. Aufgrund der Punktsymmetrie um r = 0 bzw. Fx(0) = 1/2 und wegen sin(–x) = –sin(x) gilt diese Formel im gesamten Bereich, wie die folgende Kontrollrechnung zeigt:
- $$\it F_{\it x}(\it r=\rm -2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$
- $$\it F_{\it x}(\it r=\rm -1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$
- 5. Für die Wahrscheinlichkeit, dass x zwischen -1 und +1 liegt, gilt:
- $$\rm Pr(|\it x|<\rm 1)=\it F_{\it x}(\rm 1) - \it F_{\it x}(-\rm 1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$
- Dieses Ergebnis stimmt exakt mit dem Resultat von Aufgabe A3.1(g) überein, das durch direkte Integration über die WDF ermittelt wurde.
- 6. Die VTF der diskreten Zufallsgröße y an der Stelle 0 ist die Summe der Wahrscheinlichkeiten von –2, –1 und 0, also gilt Fy(r = 0) = 0.7.