4.1:WDF, VTF und Wahrscheinlichkeit
Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch stochastischen Signaltheorie beschäftigen wir uns mit
- der Wahrscheinlichkeitsdichtefunktion (WDF),
- der Verteilungsfunktion (VTF).
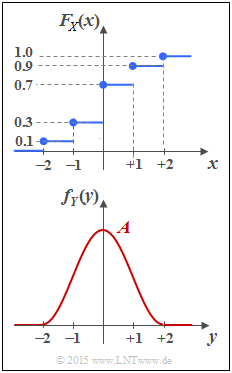
Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße X. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (a) zu bestimmen. Die Gleichung $$ {\rm Pr}(A < X \le B) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(B) - F_X(A) = $$ $$ =\hspace{-0.15cm} \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int\limits_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$
stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße X liegt in einem Intervall” aus der VTF bzw. der WDF zu berechnen.
Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |Y| ≤ 2 begrenzt ist.
Prinzipiell besteht bei der kontinuierlichen Zufallsgröße Y der gleiche Zusammenhang zwischen WDF, VTF und Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. Beispielsweise kann bei der kontinuierlichen Zufallsgröße Y in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) \hspace{0.1cm}{\rm d}y\hspace{0.05cm}$$.
Hinweis: Die Aufgabe dient zur Vorbereitung der in Kapitel 4.1 dargelegten Thematik. Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im Kapitel 3 des Buches „Stochastische Signaltheorie”. Gegeben ist zudem das folgende unbstimmte Integral: $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta)$$.
Fragebogen
Musterlösung