Exercise 4.2Z: Mixed Random Variables

Man spricht von einer gemischten Zufallsgröße, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet.

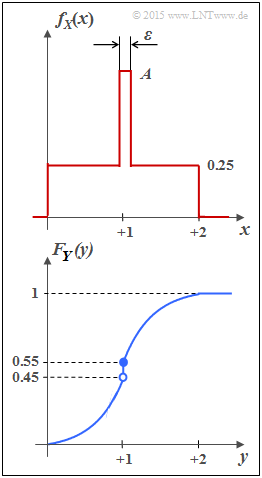
Die Zufallsgröße Y mit der Verteilungsfunktion F_Y(y) gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil. Die Wahrscheinlichkeitsdichtefunktion f_Y(y) erhält man aus F_Y(y) durch Differentiation. Aus dem Sprung bei y = 1 in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF).

In der Teilaufgabe (d) soll die differentielle Entropie h(Y) der Zufallsgröße Y ermittelt werden (in bit), wobei von folgender Gleichung auszugehen ist: $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$ In der Teilaufgabe (b) ist die differentielle Entropie h(X) der Zufallsgröße X zu berechnen, deren WDF f_X(x) oben skizziert ist. Führt man einen geeigneten Grenzübergang durch, so wird auch aus der Zufallsgröße X eine gemischte Zufallsgröße.

Hinweis: Die Aufgabe gehört zum Kapitel 4.1 des vorliegenden Buches. Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel 3.2 des Buches „Stochastische Signaltheorie”.

Fragebogen

Musterlösung

Solution

a) Das Integral über die WDF muss 1 ergeben: $$f_X(x) \hspace{0.1cm}{\rm d}x = 0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1$$ $$\Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$$ Richtig ist also der Lösungsvorschlag 2.

b) Die differentielle Entropie (in „bit”) ist wie folgt gegeben: $$h(X) = \hspace{0.1cm} \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{f_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ Wir unterteilen nun das Integral in drei Teilintegrale: $$h(X) \hspace{-0.15cm} = \hspace{-0.15cm} \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x $$ $$\ + \hspace{-0.15cm}\hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} [0.5/\varepsilon + 0.25] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$ $$=\ \hspace{-0.15cm} 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) \hspace{0.05cm}.$$ Insbesondere erhält man

für ε = 0.1:

$$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} \hspace{0.05cm},$$

für ε = 0.01:

$$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} \hspace{0.05cm}$$

für ε = 0.001:

$$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} \hspace{0.05cm}.$$ c) Alle Lösungsvorschläge sind hier zutreffend. Nach dem Grenzübergang ε → 0 erhält man für die differentielle Entropie $$h(X) \hspace{-0.15cm} = \hspace{-0.15cm} \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)]$$ $$ = \ \hspace{-0.15cm} 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty \hspace{0.05cm}.$$ Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu $$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$ Es handelt sich demzufolge um eine „gemischte” Zufallsgröße mit

einem stochastischen, gleichverteilten Anteil zwischen 0 ≤ x ≤ 2, und
einem diskreten Anteil bei x = 1 mit der Wahrscheinlichkeit 0.5.

Die Grafik zeigt links die WDF f_X(x) und rechts die Verteilungsfunktion (kurz VTF) F_X(x). 4. 5. 6. 7.

	Der VTF–Wert an der Stelle y = 1 ist 0.5.
	Y beinhaltet einen diskreten und einen kontinuierlichen Anteil..
	Der diskrete Anteil Y = 1 tritt mit 10% Wahrscheinlichkeit auf.
	Der kontinuierliche Anteil von Y ist gleichverteilt.
	Die differentiellen Entropien von X und Y sind gleich.

	f_X(x) hat nun einen kontinuierlichen und einen diskreten Anteil.
	Die differentielle Energie h(X) ist negativ.
	Der Betrag \|h(X)\| ist unendlich groß.

	A = 0.5/ε,
	A = 0.5/ε + 0.25,
	A = 1/ε.