Exercise 1.6: Non-Binary Markov Sources

• Return to book

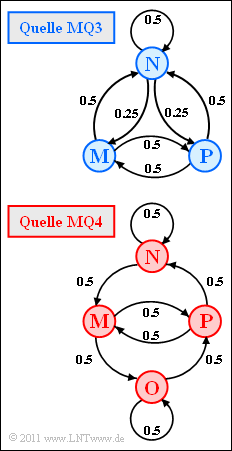
Die Grafik zeigt zwei ergodische Markovquellen (MQ):

• Die Quelle MQ3 ist durch $M = 3$ Zustände (Symbole) $\rm N$, $\rm M$, $\rm P$ gekennzeichnet. Aufgrund der Stationarität haben die Wahrscheinlichkeiten folgende Werte:

$$p_{\rm N} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P} = 1/4\hspace{0.05cm}.$$

• Bei der Quelle MQ4 ist zusätzlich der Zustand $\rm O$ möglich ⇒ $M = 4$. Aufgrund der symmetrischen Übergänge sind die stationären Wahrscheinlichkeiten alle gleich:

$$p_{\rm N} = p_{\rm M} = p_{\rm O} = p_{\rm P} = 1/4\hspace{0.05cm}.$$

Informationstheoretisch sind Markovquellen von besonderer Bedeutung, da bei diesen – und nur bei diesen – durch

• $H_1$ (Entropienäherung, nur auf den Symbolwahrscheinlichkeiten basierend), und
• $H_2$ (zweite Entropienäherung, berechenbar mit den Verbundwahrscheinlichkeiten für alle Zweiertupel)

gleichzeitig auch bestimmt sind:

• die weiteren Entropienäherungen $H_k$ mit $k = 3, 4$, ... und
• die tatsächliche Quellenentropie $H$.

Es gelten folgende Bestimmungsgleichungen:

$$H = 2 \cdot H_2 - H_1\hspace{0.05cm},\hspace{0.4cm}H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H] \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
• Bezug genommen wird insbesondere auf die Seite Nichtbinäre Markovquellen.
• Bei allen Entropien ist die Pseudoeinheit „bit/Symbol” hinzuzufügen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie die Entropienäherung $H_1$ der Markovquelle MQ3.

$H_1 \ =$ $\ \rm bit/Symbol$

2

Berechnen Sie die Entropienäherung $H_2$ der Markovquelle MQ3.

$H_2 \ =$ $\ \rm bit/Symbol$

3

Wie groß sind für MQ3 die tatsächliche Quellenentropie $H$ und die Näherungen $H_3$ und $H_4$?

$H \ =$ $\ \rm bit/Symbol$

$H_3 \ =$ $\ \rm bit/Symbol$

$H_4 \ =$ $\ \rm bit/Symbol$

4

Berechnen Sie die Entropienäherung $H_1$ der Markovquelle MQ4.

$H_1 \ =$ $\ \rm bit/Symbol$

5

Berechnen Sie die Entropienäherung $H_2$ der Markovquelle MQ4.

$H_2 \ =$ $\ \rm bit/Symbol$

6

Wie groß sind für MQ4 die tatsächliche Quellenentropie $H$ und die Näherungen $H_3$ und $H_4$?

$H \ =$ $\ \rm bit/Symbol$

$H_3 \ =$ $\ \rm bit/Symbol$

$H_4 \ =$ $\ \rm bit/Symbol$

Musterlösung

Solution

(1)  Die Symbolwahrscheinlichkeiten der ternären Markovquelle sind gegeben. Daraus lässt sich die Entropienäherung $H_1$ berechnen:

$$H_{\rm 1} = 1/2 \cdot {\rm log}_2\hspace{0.1cm} (2) + 2 \cdot 1/4 \cdot {\rm log}_2\hspace{0.1cm}(4 ) \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(2)  Die Verbundwahrscheinlichkeit ist $p_{\rm XY} = p_{\rm X} \cdot p_{\rm Y|X}$, wobei $p_{\rm X}$ die Symbolwahrscheinlichkeit von $\rm X$ angibt und $p_{\rm Y|X}$ die bedingte Wahrscheinlichkeit für $\rm Y$, unter der Voraussetzung, dass vorher $\rm X$ aufgetreten ist.

$\rm X$ und $\rm Y$ sind hier Platzhalter für die Symbole $\rm N$, $\rm P$ und $\rm M$. Dann gilt:

$$p_{\rm NN} = 1/2 \cdot 1/2 = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm PP} = 1/4 \cdot 0 = 0\hspace{0.05cm},\hspace{0.2cm}p_{\rm MM} = 1/4 \cdot 0 = 0 \hspace{0.05cm},$$

$$p_{\rm NP} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm PM} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm MN} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$

$$p_{\rm NM} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm MP} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm PN} = 1/4 \cdot 1/2 = 1/8$$

$$\Rightarrow \hspace{0.3cm} H_{\rm 2} = {1}/{2} \cdot \left [ 1/4 \cdot {\rm log}_2\hspace{0.1cm}( 4) + 6 \cdot 1/8 \cdot {\rm log}_2\hspace{0.1cm} (8) \right ] \hspace{0.15cm} \underline {= 1.375 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(3)  Da MQ3 Markoveigenschaften aufweist, können aus $H_1$ und $H_2$ alle Entropienäherungen $H_k$ (für $k = 3, 4,$ ... ) angegeben werden und auch der Grenzwert $H =H_\infty$ für $k \to \infty$:

$$H = 2 \cdot H_2 - H_1 = 2\cdot 1.375 - 1.5 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/Symbol}}\hspace{0.05cm},$$

$$H_3 \hspace{0.1cm} = \hspace{0.1cm}= (H_1 + 2 \cdot H)/3 = (1.5 + 2 \cdot 1.25)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/Symbol}}\hspace{0.05cm},$$

$$H_4 = (H_1 + 3 \cdot H)/4 = (1.5 + 3 \cdot 1.25)/4 \hspace{0.15cm} \underline {= 1.3125 \,{\rm bit/Symbol}}\hspace{0.05cm}.$$

Die 10. Entropienäherung unterscheidet sich noch immer, wenn auch nur geringfügig (um 2%) vom Endwert $H = 1.25 \, \rm bit/Symbol$:

$$H_{10} = (H_1 + 9 \cdot H)/10 = (1.5 + 9 \cdot 1.25)/10 {= 1.275 \,{\rm bit/Symbol}}\hspace{0.05cm}.$$

(4)  Entsprechend der Angabe sind bei MQ3 die $M = 4$ Symbole gleichwahrscheinlich. Daraus folgt:

$$H_{\rm 1} = H_{\rm 0} = {\rm log}_2\hspace{0.1cm} (4) \hspace{0.15cm} \underline {= 2 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(5)  Von den $M^2 = 16$ möglichen Zweiertupeln sind acht Kombinationen nicht möglich:

$$\rm NP, NO, PP, PO, OM, ON, MM, MN.$$

Die acht weiteren Kombinationen (Zweiertupel) ergeben jeweils den Verbundwahrscheinlichkeitswert $1/8$, wie an zwei Beispielen gezeigt wird:

$$p_{\rm NN} = p_{\rm N} \cdot p_{\rm N\hspace{0.01cm}|\hspace{0.01cm}N} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$

$$p_{\rm MP} = p_{\rm M} \cdot p_{\rm P\hspace{0.01cm}|\hspace{0.01cm}M} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \left [ 8 \cdot 1/8 \cdot {\rm log}_2\hspace{0.1cm} (8) \right ] \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(6)  Aufgrund der Markoveigenschaft gilt hier:

$$H = 2 \cdot H_2 - H_1 = 2\cdot 1.5 - 2 \hspace{0.15cm} \underline {= 1 \,{\rm bit/Symbol}}\hspace{0.05cm},$$

$$H_3 = (H_1 + 2 \cdot H)/3 = (2 + 2 \cdot 1)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/Symbol}}\hspace{0.05cm},$$

$$H_4 = (H_1 + 3 \cdot H)/4 = (2 + 3 \cdot 1)/4 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/Symbol}}\hspace{0.05cm}.$$

Auch hier unterscheidet sich die 10. Näherung noch deutlich, nämlich um $10\%$, vom Endwert:

$$H_{10} = (H_1 + 9 \cdot H)/10 = (2 + 9 \cdot 1)/10 {= 1.1 \,{\rm bit/Symbol}}\hspace{0.05cm}.$$

Eine Abweichung um $2\%$ ergibt sich hier erst für $k = 50$. Zum Vergleich: Bei der Markovquelle MQ3 wurde diese Annäherung bereits mit $k = 10$ erreicht.