Exercise 5.5: Multi-User Interference

Wir betrachten die PN–Modulation mit folgenden Parametern:

Die Spreizung erfolgt mit der M–Sequenz $(45)_{oktal}$ vom Grad G = 5. Die Periodenlänge ist somit $P = 2^5 –1 = 31$.
Der AWGN–Parameter wird mit $10 · lg (E_B/N_0) = 5 dB$ festgelegt. Daraus folgt $E_B/N_0 = 3.162 = 1/0.316$.
Die Bitfehlerwahrscheinlichkeit beträgt ohne interferierende Teilnehmer im gleichen Frequenzband

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2E_{\rm B}}/{N_{\rm 0}}}\right ) \approx {\rm Q} \left ( \sqrt{2 \cdot 3.162}\right ) = {\rm Q} \left ( 2.515 \right ) \approx 6 \cdot 10^{-3} \hspace{0.05cm}.$$

Da ohne interferierende Teilnehmer alle Nutzabtastwerte gleich $±s_0$ sind (Nyquistsystem), gilt für die Fehlerwahrscheinlichkeit in gleicher Weise:

$$p_{\rm B} = {\rm Q} \left ( {s_0}/{\sigma_d}\right ) \hspace{0.05cm}.$$ $σ_d$ bezeichnet den Rauscheffektivwert vor dem Entscheider, herrührend vom AWGN–Rauschen.

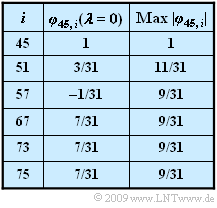
In dieser Aufgabe soll untersucht werden, wie die Bitfehlerwahrscheinlichkeit durch einen einzigen zusätzlichen Teilnehmer verändert wird. Die Spreizfolgen der interferierenden Teilnehmer seien ebenfalls durch P = 31 festgelegt. Zur Verfügung stehen die PN–Generatoren mit den Oktalkennungen (45), (51), (57), (67), (73) und (75). In der Tabelle sind die PKKF–Werte für λ = 0 angegeben, desweiteren auch der jeweilige Maximalwert für eine andere Anfangsphase: $$ {\rm Max}\,\,|{\it \varphi}_{45,\hspace{0.05cm}i}| = \max_{\lambda} \,\,|{\it \varphi}_{45,\hspace{0.05cm}i}(\lambda)| \hspace{0.05cm}.$$ Der Sonderfall $φ_{45, 45}(λ = 0)$ gibt den PAKF–Wert der Spreizfolge mit der Oktalkennung (45) an.

Im Verlauf dieser Aufgabe und in der Musterlösung werden folgende Signale erwähnt:

$q(t)$: binäres bipolares Quellensignal, Symboldauer T,
$c(t)$: ±1–Spreizsignal, Chipdauer $T_c$,
$s(t) = q(t) · c(t)$: bandgespreiztes Sendesignal, Amplitude $±s_0$, Chipdauer $T_c$,
$n(t)$: AWGN–Rauschen, festgelegt durch den Quotienten $E_B/N_0$,
$i(t)$: Interferenzsignal des störenden Teilnehmers,
$r(t) = s(t) + n(t) + i(t)$: Empfangssignal,
$b(t)= r(t) · c(t)$: bandgestauchtes Signal,
$d(t)$: Detektionssignal nach Integration von $b(t)$ über die Symboldauer T,
$υ(t)$: Sinkensignal, der Vergleich mit $q(t)$ liefert die Fehlerwahrscheinlichkeit.

Hinweise:

Die Aufgabe gehört zum Kapitel Spreizfolgen für CDMA.
Bezug genommen wird insbesondere auf den Abschnitt Codes mit variablem Spreizfaktor im Theorieteil.
Wir möchten Sie gerne auch auf das Interaktionsmodul OVSF hinweisen.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 5.4. Für die sog. Q-Funktion kann von folgenden Näherungen ausgegangen werden: $$ {\rm Q} (2) \approx 0.02275, \hspace{0.2cm}{\rm Q} (3) \approx 0.00135, \hspace{0.2cm}{\rm Q} (5) \approx 2.45 \cdot 10^{-7} \hspace{0.05cm}.$$

Fragebogen

$σ_d/s_0$ =

$i(t) = (45)_{oktal}: p_B$ =

$i(t) = (75)_{oktal}: p_B$ =

	Mit der Oktalkennung (51) ist $p-B = 0.001$ möglich.
	Mit der Oktalkennung (57) ist $p-B = 0.007$ möglich.
	Mit der Oktalkennung (67) ist $p-B = 0.012$ möglich.

Musterlösung

Solution

1. Aus den beiden vorne angegebenen Gleichungen folgt direkt: $$p_{\rm B} = {\rm Q}(2.515) = {\rm Q}({s_0}/{\sigma_d}) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \frac{\sigma_d}{s_0} = \frac{1}{2.515} = 0.398 \hspace{0.15cm}\underline {\approx 0.4} \hspace{0.05cm}.$$ Man könnte diese Größe aber auch über die allgemeinere Gleichung $$ \sigma_d^2 = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty} |H_{\rm I}(f) |^2 \,\,{\rm d} {\it f}\hspace{0.05cm} = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty}{\rm si}^2(\pi f T)\,\,{\rm d} {\it f} = \frac{N_0}{2T } \hspace{0.05cm}.$$ berechnen. Hierbei beschreibt $H_I(f)$ den Integrator im Frequenzbereich. Mit $E_B = s_0^2 · T$ ergibt sich $$\frac{\sigma_d^2}{s_0^2} = \frac{N_0}{2 \cdot s_0^2 \cdot T } = \frac{N_0}{2 E_{\rm B} } = \frac{0.316}{2 } = 0.158\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\sigma_d}/{s_0} = 0.398 \approx 0.4 \hspace{0.05cm}.$$

2. Benutzt der interferierende Teilnehmer die gleiche M–Sequenz $(45)_{oct}$ wie der betrachtete Nutzer, so sind die (normierten) Detektionsnutzabtastwerte gleich +2 (zu 25%), –2 (zu 25%) und 0 (zu 50%). Bei $d(νT) = ±2$ wird die Fehlerwahrscheinlichkeit für den betrachteten Teilnehmer signifikant verkleinert. In diesem Fall übertragen beide Nutzer das gleiche Bit (+1 oder –1) und der Abstand von der Schwelle wird verdoppelt: $$ p_{\rm B}\,\,[{\rm falls}\,\, d (\nu T) = \pm 2s_0 ] = {\rm Q} \left ( 2 \cdot 2.515 \right ) = {\rm Q} \left ( 5.03 \right ) \approx 2.45 \cdot 10^{-7} \approx 0 \hspace{0.05cm}.$$ Ist dagegen $d(νT) = 0$ (zum Beispiel, wenn $a_1(s) = +1$ und $a_1(i) = –1$ gilt oder umgekehrt), so löschen sich die Signale vollständig aus und man erhält $$p_{\rm B}\,\,[{\rm falls}\,\, d (\nu T) = 0 ] = {\rm Q} \left ( 0 \right ) = 0.5 \hspace{0.05cm}.$$ Durch Mittelung über diese beiden gleichwahrscheinlichen Möglichkeiten ergibt sich so für die mittlere Bitfehlerwahrscheinlichkeit: $$p_{\rm B}= 0.5 \cdot 2.45 \cdot 10^{-7}+ 0.5 \cdot 0.5 \hspace{0.15cm}\underline {\approx 0.25} \hspace{0.05cm}.$$ 3. Wir betrachten zunächst nur den Nutzanteil ⇒ $n(t) = 0$. Außerdem beschränken wir uns auf das erste Datensymbol und setzen den Amplitudenkoeffizienten $a_{1(s)} = +1$ voraus. Dann gilt innerhalb dieses Datenbits $s(t) = c_{45}(t)$. Ist der Koeffizient $a_{1(i)}$ des interferierenden Teilnehmers ebenfalls +1, so erhält man für die vorne spezifizierten Signale im Zeitintervall von 0 bis T: $$ r(t) = c_{45}(t) + c_{75}(t)\hspace{0.05cm},$$ $$b(t) = r(t) \cdot c_{45}(t) = \left [c_{45}(t) + c_{75}(t) \right ] \cdot c_{45}(t) = 1+ c_{45}(t) \cdot c_{75}(t) \hspace{0.05cm},$$ $$ d (T) = \frac{1}{T} \cdot \int_{0 }^{ T} b (t )\hspace{0.1cm} {\rm d}t = 1 + {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ Hierbei bezeichnet $φ_{45, 75}(τ)$ die PKKF zwischen den Spreizfolgen mit den Oktalkennungen (45) und (75), die in der Tabelle auf der Angabenseite zu finden sind.

Entsprechend gilt für den Detektionsnutzabtastwert unter der Voraussetzung $a_{1(s)} = +1$ und $a_{1(i)} = –1$: $$d (T) = 1 - {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ Aus Symmetriegründen liefern die Koeffizienten $a_{1(s)} = –1$, $a_{1(i)} = –1$ sowie $a_{1(s)} = –1$, $a_{1(i)} = +1$ die genau gleichen Beiträge für die Bitfehlerwahrscheinlichkeit wie $a_{1(s)} = +1$, $a_{1(i)} = +1$ bzw. $a_{1(s)} = +1$, $a_{1(i)} = –1$, wenn man zudem das AWGN–Rauschen berücksichtigt.

Mit dem Ergebnis der Teilaufgabe a) und $φ_{45, 75}(λ = 0) = 7/31$ erhält man somit näherungsweise: $$p_{\rm B} = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1+ 7/31}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{1- 7/31}{0.4} \right ) =$$ $$ = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1.225}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{0.775}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( 3.06 \right ) + \frac{1}{2} \cdot {\rm Q} \left ( 1.94 \right ) \approx $$ $$ \approx \frac{1}{2} \cdot \left [{\rm Q} \left ( 3 \right ) + {\rm Q} \left ( 2 \right ) \right ] = \frac{1}{2} \cdot \left [0.00135 + 0.02275 \right ] \hspace{0.15cm}\underline {= 0.012}\hspace{0.05cm}.$$

4. Möglich sind die Lösungsvorschläge 2 und 3. Der PKKF–Wert $φ_{45, 57}(λ = 0)$ ist betragsmäßig nur 1/31 und damit ist die Fehlerwahrscheinlichkeit nur geringfügig größer als 0.6%. Die Folge $(67)_{oktal}$ führt dagegen zur gleichen PKKF wie die Folge $(75)_{oktal}$.

Ohne störenden Teilnehmer gilt entsprechend dem Angabenblatt; $p_B = 0.6%$. Mit Interferenz kann dieser Wert nicht unterschritten werden ⇒ Lösungsvorschlag 1 ist nicht möglich.