Exercise 3.10Z: Amplitude and Angle Modulation in Comparison
Betrachtet wird die Übertragung eines Cosinussignals mit Amplitudenmodulation (AM) und Winkelmodulation (WM). Es gelten folgende Randbedingungen:
- Nachrichtenfrequenz $f_{\rm N} = 10 \ \rm kHz$,
- Sendeleistung $P_{\rm S} = 100 \ \rm kW$,
- Kanaldämpfungsfaktor $20 · \lg α_{\rm K} = -120 \ \rm dB$,
- Rauschleistungsdichte $N_0 = 10^{–16} \ \rm W/Hz$.
Diese Systemparameter werden zweckmäßigerweise zur gemeinsamen Leistungskenngröße
- $$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
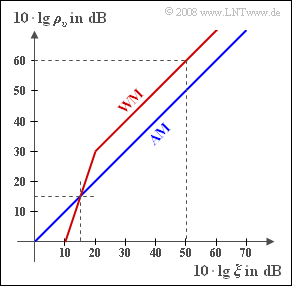
zusammengefasst. Die Grafik zeigt den sich ergebenden Sinken–Störabstand $10 · \lg ρ_v$ in Abhängigkeit der logarithmierten Leistungskenngröße $ξ$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Rauscheinfluss bei Winkelmodulation.
- Bezug genommen wird aber auch auf den Abschnitt Sinken-SNR und Leistungskenngröße sowie auf das Kapitel Frequenzmodulation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Es gelten folgende Beziehungen:
- $$\rho_{v } = \left\{ \begin{array}{c} \xi \\ {\eta^2}/2 \cdot\xi \\ 3{\eta^2}/2 \cdot\xi \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}l} {\rm ZSB/ESB-AM \hspace{0.15cm}ohne \hspace{0.15cm}Tr\ddot{a}ger} \hspace{0.05cm}, \\ {\rm PM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta } \hspace{0.05cm}, \\ {\rm FM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta }\hspace{0.05cm}. \\ \end{array}$$
- Die Bandbreiten $B_{\rm K}$ bei Winkelmodulation sind gemäß der Carson–Regel so zu wählen, dass ein Klirrfaktor $K < 1\%$ garantiert werden kann:
- $$ B_{\rm K} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.05cm}.$$
Fragebogen
Musterlösung
2. Aus der Grafik ist zu entnehmen, dass beim AM–System $ρ_υ = ξ$ gilt. Damit ist auch $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$
3. Es handelt sich um eine ZSB–AM oder ESB–AM ohne Träger, das heißt, richtig sind die ersten drei Lösungsvorschläge. Dagegen scheiden die ZSB–AM und die ESB–AM mit Träger aus. In diesen Fällen würde $ρ_υ$ stets kleiner als $ξ$ sein.
4.Bei der ZSB–AM muss $B_K ≥ 2 · f_N = 20 kHz$ gelten.
5. Aus der Grafik erkennt man, dass ab etwa $20 dB$ gilt:
$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 10 \cdot {\rm lg} \hspace{0.15cm}\xi + 10\,{\rm dB}. \hspace{0.3cm}{\rm Mit}\hspace{0.15cm}10 \cdot {\rm lg} \hspace{0.15cm}\xi = 50\,{\rm dB}\hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 60\,{\rm dB}}.$$
6. Bei Phasenmodulation gilt: $$ \rho_{v }= \frac{\eta^2}{2} \cdot \xi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta^2 = \frac{2 \cdot \rho_{v }}{\xi} = 20\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 4.47 \hspace{0.05cm}.$$ Damit muss für die Kanalbandbreite unter der Voraussetzung K < 1% gelten: $$B_{\rm K} \ge 2 \cdot f_{\rm N} \cdot (\eta +2) = 20\,{\rm kHz}\cdot 6.47 \hspace{0.15cm}\underline { \approx 130\,{\rm kHz}}\hspace{0.05cm}.$$
7.Hier genügt ein kleinerer Modulationsindex und damit auch eine kleinere Bandbreite: $${3}/{2}\cdot \eta^2 = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 2.58 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}B_{\rm K} = 20\,{\rm kHz}\cdot 4.58 \hspace{0.15cm}\underline {\approx 91.6\,{\rm kHz}}\hspace{0.05cm}.$$ 8. In der Grafik erkennt man den so genannten FM–Knick. Für $10 · lg ξ = 15 dB$ erhält man für das WM–System genau das gleiche Sinken–SNR wie für das AM–System. Die Sendeleistung kann also um $35 dB$ kleiner sein als $100 kW$: $$ 10 \cdot {\rm lg} \hspace{0.15cm}\frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}= -35\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}\approx 0.0003\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm S,\hspace{0.05cm}min} \hspace{0.15cm}\underline {\approx 0.03\,{\rm kW}}\hspace{0.05cm}.$$