Burst Error Channels

1. Digital Signal Transmission
2. Digitale Kanalmodelle
3. Burst Error Channels

• Previous page
• Next page

• Previous page
• Next page

Kanalmodell nach Gilbert–Elliott

Dieses auf E. N. Gilbert [Gil60] und E. O. Elliott [Ell63] zurückgehende Kanalmodell eignet sich zur Beschreibung und Simulation von digitalen Übertragungssystemen mit Bündelfehlercharakteristik.

Gilbert–Elliott–Kanalmodell

Das Gilbert–Elliott–Modell (Kurzbezeichnung: GE–Modell) lässt sich wie folgt charakterisieren:

• Die unterschiedliche Übertragungsqualität zu unterschiedlichen Zeiten wird durch eine endliche Anzahl $g$ von Kanalzuständen $(Z_1, Z_2, \text{...}, Z_g)$ ausgedrückt.
  

• Die in Wirklichkeit fließenden Übergänge der Störintensität – im Extremfall von völlig fehlerfreier Übertragung bis hin zum Totalausfall – werden beim GE–Modell durch feste Wahrscheinlichkeiten in den einzelnen Kanalzuständen approximiert.
  

• Die Übergänge zwischen den $g$ Zuständen erfolgen gemäß einem Markovprozess (1. Ordnung) und werden durch $g \cdot (g-1)$ Übergangswahrscheinlichkeiten gekennzeichnet. Zusammen mit den $g$ Fehlerwahrscheinlichkeiten in den einzelnen Zuständen gibt es somit $g^2$ freie Modellparameter.
  

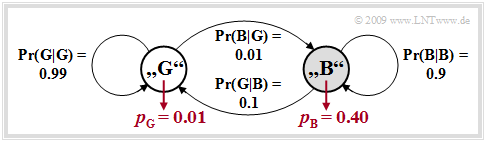
• Aus Gründen der mathematischen Handhabbarkeit beschränkt man sich meist auf $g = 2$ Zustände und bezeichnet diese mit $\rm G$ („GOOD”) und $\rm B$ („BAD”). Meist wird die Fehlerwahrscheinlichkeit im Zustand $\rm G$ sehr viel kleiner sein als im Zustand $\rm B$.
  

• Im Folgenden benutzen wir diese beiden Fehlerwahrscheinlichkeiten $p_{\rm G}$ und $p_{\rm B}$, wobei $p_{\rm G} < p_{\rm B}$ gelten soll, sowie die Übergangswahrscheinlichkeiten ${\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm}G)$ und ${\rm Pr}(G\hspace{0.05cm}|\hspace{0.05cm}B)$. Damit sind auch die beiden anderen Übergangswahrscheinlichkeiten festgelegt:

\[{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) = 1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G), \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B) = 1 - {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{0.05cm}.\]

Kanalmodell nach Gilbert–Elliott (2)

Beispielhaft betrachten wir nun das GE–Modell mit den Parametern

\[p_{\rm G} = 0.01, \hspace{0.2cm}p_{\rm B} = 0.4, \hspace{0.2cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) = 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.\]

Betrachtetes GE–Modell

Die nachfolgende Grafik zeigt eine dazugehörige (mögliche) Fehlerfolge der Länge N = 800.

Befindet sich das GE–Modell im Zustand „BAD”, so erkennt man dies an der grauen Hinterlegung. Die Wahrscheinlichkeiten, dass sich die Markovkette im Zustand „G” bzw. „B” befindet, lassen sich aus der vorausgesetzten Homogenität und Stationarität berechnen. Man erhält mit den obigen Zahlenwerten:

\[w_{\rm G} \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr(im\hspace{0.15cm} Zustand \hspace{0.15cm}G)}= \frac{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} = {10}/{11}\hspace{0.05cm},\] \[w_{\rm B} \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr(im\hspace{0.15cm} Zustand \hspace{0.15cm}B)}= \frac{{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.11}{0.1 + 0.01} = {1}/{11}\hspace{0.05cm}.\]

Damit kann auch die mittlere Fehlerwahrscheinlichkeit des GE–Modells ermittelt werden:

\[p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{p_{\rm G} \cdot {\rm Pr}({\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm}.\]

Insbesondere gilt für das hier beispielhaft betrachtete Modell:

\[p_{\rm M} ={10}/{11} \cdot 0.01 +{1}/{11} \cdot 0.4 = {1}/{22} \approx 4.55\%\hspace{0.05cm}.\]

Zur Simulation einer GE–Fehlerfolge wird zwischen den Zuständen „G” und „B” entsprechend den vier Übergangswahrscheinlichkeiten umgeschaltet. Beim ersten Aufruf erfolgt die Auswahl des Zustandes zweckmäßigerweise entsprechend den Wahrscheinlichkeiten w_G und w_B.

Zu jedem Taktzeitpunkt wird genau ein Element der Fehlerfolge 〈e_ν〉 entsprechend der aktuellen Fehlerwahrscheinlichkeit (p_G bzw. p_B) erzeugt. Die Simulation des Fehlerabstandes ist hier nicht anwendbar, da ein Zustandswechsel nach jedem Symbol (und nicht nur nach einem Fehler) möglich ist.

Fehlerabstandsverteilung des GE–Modells

In [Hub82] finden sich die analytischen Berechnungen

• der Wahrscheinlichkeit des Fehlerabstandes k:

\[{\rm Pr}(a=k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm G}) + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \cdot (1- \beta_{\rm B})\hspace{0.05cm},\]

• der Fehlerabstandsverteilung:

\[V_a(k) = {\rm Pr}(a \ge k) = \alpha_{\rm G} \cdot \beta_{\rm G}^{\hspace{0.05cm}k-1} + \alpha_{\rm B} \cdot \beta_{\rm B}^{\hspace{0.05cm}k-1} \hspace{0.05cm}.\]

Hierbei sind folgende Hilfsgrößen verwendet:

\[u_{\rm GG} \hspace{-0.1cm} = \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\] \[u_{\rm BB} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}\]

\[\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},\] \[\hspace{0.8cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]

\[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}\]

\[\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]

Die angegebenen Gleichungen sind das Ergebnis umfangreicher Matrizenoperationen.

Fehlerabstandsverteilung von GE– und BSC–Modell

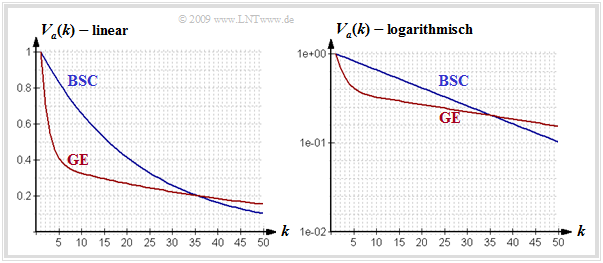
• Die Abbildung zeigt die Fehlerabstandsverteilung (FAV) des GE–Modells (rote Kurve) in linearer und logarithmischer Darstellung für Pr(G|B) = 0.1, Pr(B|G) = 0.01, p_G = 0.001 und p_B = 0.4.
  

• Zum Vergleich ist auch der Verlauf von V_a(k) für das BSC–Modell mit der gleichen mittleren Fehlerwahrscheinlichkeit p_M = 4.5% als blaue Kurve eingezeichnet.
  

Fehlerkorrelationsfunktion des GE–Modells

Für die Fehlerkorrelationsfunktion (FKF) ergibt sich mit der mittleren Fehlerwahrscheinlichkeit p_M, den Übergangswahrscheinlichkeiten Pr(B|G) und Pr(G|B) sowie den Fehlerwahrscheinlichkeiten p_G und p_B in den zwei Zuständen „G” und „B” nach umfangreichen Matrizenoperationen der relativ einfache Ausdruck

\[\varphi_{e}(k) = \left\{ \begin{array}{c} p_{\rm M} \\ p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) (p_{\rm M} - p_{\rm G}) [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^k \end{array} \right.\quad \begin{array}{*{1}c} f{\rm \ddot{u}r }\hspace{0.15cm}k = 0 \hspace{0.05cm}, \\ f{\rm \ddot{u}r }\hspace{0.15cm} k > 0 \hspace{0.05cm}.\\ \end{array}\]

Der nur für „erneuernde Modelle” gültige Zusammenhang zwischen FKF und FAV ist hier nicht gegeben (GE–Modell ist nicht erneuernd!)  ⇒  Zur Berechnung unbedingt φ_e(k) = E[e_ν · e_ν+k] verwenden.

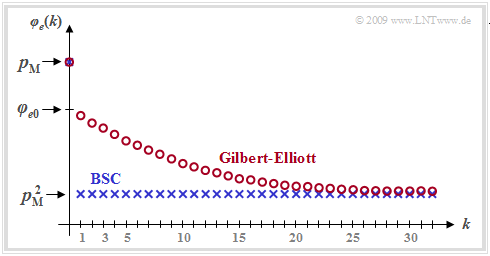
In der Grafik ist ein beispielhafter FKF–Verlauf des GE–Modells mit roten Kreisen markiert eingetragen. Während beim gedächtnislosen Kanal (BSC–Modell, blaue Kurve) alle FKF–Werte φ_e(k ≠ 0) gleich p_M² sind, nähern sich die FKF–Werte beim Bündelfehlerkanal diesem Endwert deutlich langsamer.

Fehlerkorrelationsfunktion von GE-Modell (Kreise) und BSC-Modell (Kreuze)

Weiter erkennt man aus dieser Darstellung:

• Beim Übergang von k = 0 nach k = 1 tritt eine gewisse Unstetigkeit auf. Während φ_e(k = 0) = p_M ist, ergibt sich mit der für k > 0 gültigen zweiten Gleichung für k = 0 folgender extrapolierter Wert:

\[\varphi_{e0} = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G})\hspace{0.05cm}.\]

• Ein quantitatives Maß für die Länge der statistischen Bindungen ist die Korrelationsdauer D_K, die allgemein als die Breite eines flächengleichen Rechtecks mit der Höhe φ_e0 – p_M² definiert ist:

\[D_{\rm K} = \frac{1}{\varphi_{e0} - p_{\rm M}^2} \cdot \sum_{k = 1 }^{\infty}\hspace{0.1cm} [\varphi_{e}(k) - p_{\rm M}^2]\hspace{0.05cm}.\]

• Beim Gilbert–Elliott–Modell erhält man hierfür den einfachen, analytisch angebbaren Ausdruck

\[D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 \hspace{0.05cm}.\]

• D_K ist umso größer, je kleiner Pr(B|G) und Pr(G|B) sind (also Zustandswechsel selten auftreten). Für das BSC–Modell (p_B = p_G = p_M, D_K = 0) ist die Gleichung nicht anwendbar.
  

Kanalmodell nach McCullough

Der wesentliche Nachteil des GE–Modells ist, dass damit eine Fehlerabstandssimulation nicht möglich ist. Wie in der Aufgabe A5.5 herausgearbeitet wurde, hat diese gegenüber der symbolweisen Generierung der Fehlerfolge 〈e_ν〉 große Vorteile hinsichtlich Rechengeschwindigkeit und Speicherbedarf.

McCullough [McC68] hat das drei Jahre zuvor von Gilbert und Elliott entwickelte Modell dahingehend modifiziert, dass eine Fehlerabstandssimulation in den beiden Zustände „GOOD” und „BAD” jeweils für sich anwendbar ist. Die Grafik zeigt unten das Modell von McCullough, im Folgenden als MC–Modell bezeichnet, während oben das GE–Modell nach Umbenennung der Übergangswahrscheinlichkeiten ⇒ p(B|G) = Pr(B|G), p(G|B) = Pr(G|B) usw. dargestellt ist.

[[File:P ID1840 Dig T 5 3 S4a version1.png|center|frame|Kanalmodelle nach Gilbert–Elliott (oben) und McCullough (unten)|class=fit]

Zwischen den beiden Modellen bestehen viele Gemeinsamkeiten und einige wenige Unterschiede:

• Das McCullough–Kanalmodell beruht wie das Gilbert–Elliott–Modell auf einem Markovprozess erster Ordnung mit den beiden Zuständen „G” (GOOD) und „B” (BAD). Hinsichtlich der Modellstruktur ist kein Unterschied feststellbar.
  

• Der wesentliche Unterschied zum GE–Modell besteht darin, dass ein Zustandswechsel zwischen „G” und „B” jeweils nur nach einem Fehler – also einer „1” in der Fehlerfolge – möglich ist. Dies ermöglicht eine Fehlerabstandssimulation.
  

• Die vier frei wählbaren GE–Parameter p_G, p_B, p(B|G) und p(G|B) können – wie auf der nächsten Seite gezeigt – so in die MC–Parameter q_G, q_B, q(B|G) und q(G|B) umgerechnet werden, dass eine in ihren statistischen Eigenschaften gleiche Fehlerfolge wie beim GE–Modell erzeugt wird.
  

• Beispielsweise bezeichnet q(B|G) die Übergangswahrscheinlichkeit von dem Zustand „G” in den Zustand „B” unter der Voraussetzung, dass im Zustand „G” gerade ein Fehler aufgetreten ist. Der GE–Parameter p(B|G) kennzeichnet diese Übergangswahrscheinlichkeit ohne Zusatzbedingung.
  

Kanalmodell nach McCullough (2)

Die Abbildung zeigt oben eine beispielhafte Fehlerfolge des GE–Modells mit den Parametern p_G = 0.01, p_B = 0.4, p(G|B) = 0.1 und p(B|G) = 0.01. Man erkennt, dass ein Zustandswechsel von „G” (ohne Hinterlegung) nach „B” (graue Hinterlegung) und umgekehrt zu jedem Zeitpunkt ν möglich ist – also auch dann, wenn e_ν gleich 0 ist.

Fehlerfolge des GE–Modells (oben) und des MC–Modells (unten)

Die Zusammenhänge zwischen den beiden Modellen lassen sich wie folgt zusammenfassen:

• Bei der unten dargestellten Fehlerfolge des McCullough–Modells ist im Gegensatz zur oberen Folge ein Zustandswechsel zum Zeitpunkt ν nur bei e_ν = 1 möglich.
  

• Dies hat den Vorteil, dass man bei einer Fehlerfolgensimulation die Fehler nicht „step–by–step” generieren muss, sondern die schnellere Fehlerabstandssimulation nutzen kann ⇒  Aufgabe A5.5.
  

• Die Parameter des GE–Modells können derart in entsprechende MC–Parameter umgerechnet werden, dass beide Modellen äquivalent sind.
  

• Das bedeutet, dass die MC–Fehlerfolge exakt gleiche statistische Eigenschaften besitzt wie die GE–Fehlerfolge. Es bedeutet aber nicht, dass die beiden Fehlerfolgen identisch sind.
  
  

Die Umrechnung der GE– in die MC–Parameter wird auf der nächsten Seite beschrieben und in der Aufgabe A5.7 an einem einfachen Beispiel verdeutlicht. In der Aufgabe Z5.7 wird weiter gezeigt, wie die mittlere Fehlerwahrscheinlichkeit, die Fehlerabstandsverteilung, die Fehlerkorrelationsfunktion und die Korrelationsdauer des MC–Modells direkt aus den q–Parametern ermittelt werden können.

Kanalmodell nach McCullough (3)

Die Parameter des äquivalenten MC–Modells sind aus den GE–Parametern wie folgt berechenbar:

\[q_{\rm G} =1-\beta_{\rm G}\hspace{0.05cm}, \hspace{0.2cm}q_{\rm B} = 1-\beta_{\rm B}\hspace{0.05cm}.\]

\[q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) =\frac{\alpha_{\rm B} \cdot[{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, \hspace{0.5cm} q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) = \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.\]

Hierbei sind wieder die folgenden Hilfsgrößen verwendet:

\[u_{\rm GG} \hspace{-0.1cm} = \hspace{-0.1cm}{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\rm G}) \hspace{0.05cm},\hspace{0.2cm} {\it u}_{\rm GB} ={\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) \cdot (1-{\it p}_{\hspace{0.03cm} \rm G}) \hspace{0.05cm},\] \[u_{\rm BB} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B}) \hspace{0.05cm},\hspace{0.29cm} {\it u}_{\rm BG} ={\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) \cdot (1-{\it p}_{\hspace{0.03cm}\rm B})\hspace{0.05cm}\]

\[\Rightarrow \hspace{0.3cm} \beta_{\rm G} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} + \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2} \hspace{0.05cm},\] \[\hspace{0.7cm}\beta_{\rm B} \hspace{-0.1cm} = \hspace{-0.1cm}\frac{u_{\rm GG} + u_{\rm BB} - \sqrt{(u_{\rm GG} - u_{\rm BB})^2 + 4 \cdot u_{\rm GB}\cdot u_{\rm BG}}}{2}\hspace{0.05cm}.\]

\[x_{\rm G} =\frac{u_{\rm BG}}{\beta_{\rm G}-u_{\rm BB}} \hspace{0.05cm},\hspace{0.2cm} x_{\rm B} =\frac{u_{\rm BG}}{\beta_{\rm B}-u_{\rm BB}}\]

\[\Rightarrow \hspace{0.3cm} \alpha_{\rm G} = \frac{(w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}\cdot x_{\rm G})( x_{\rm B}-1)}{p_{\rm M} \cdot( x_{\rm B}-x_{\rm G})} \hspace{0.05cm}, \hspace{0.2cm}\alpha_{\rm B} = 1-\alpha_{\rm G}\hspace{0.05cm}.\]

Fehlerfolge des GE–Modells (oben) und des MC–Modells (unten)

• GE–Parameter:     p_G = 0.01, p_B = 0.4, p(G|B) = 0.1 und p(B|G) = 0.01.
  

• MC–Parameter:   q_G = 0.0186, q_B = 0.4613, q(G|B) = 0.2240 und q(B|G) = 0.3602.
  

Bündelfehlerkanalmodell nach Wilhelm

Dieses Modell geht auf Claus Wilhelm zurück und wurde ab Mitte der 1960er Jahre aus empirischen Messungen zeitlicher Folgen von Bitfehlern entwickelt. Es beruht auf Tausenden von Messstunden in Übertragungskanälen ab 200 bit/s mit analogem Modem bis hin zu 2.048 Mbit/s über ISDN. Ebenso wurden Seefunkkanäle bis zu 7500 Kilometern im Kurzwellenbereich vermessen.

Aufgezeichnet wurden Blöcke der Länge n. Daraus wurde die jeweilige Blockfehlerrate h_B(n) ermittelt. Ein Blockfehler liegt bereits dann vor, wenn auch nur eines der n Symbole verfälscht wurde. Wohl wissend, dass die Blockfehlerrate h_B nur für n → ∞ exakt mit der Blockfehlerwahrscheinlichkeit p_B übereinstimmt, setzen wir bei der folgenden Beschreibung p_B(n) ≈ h_B(n).

Beispielhafte Funktionsverläufe p_B(n)

Bei einer Vielzahl von Messungen wurde immer wieder die Tatsache bestätigt, dass der Verlauf p_B(n) in doppelt–logarithmischer Darstellung im unteren Bereich lineare Anstiege aufweisen (siehe Grafik). Es gilt also für n ≤ n^∗:

\[{\rm lg} \hspace{0.1cm}p_{\rm B}(n) = {\rm lg} \hspace{0.1cm}p_{\rm S} + \alpha \cdot {\rm lg} \hspace{0.1cm}n\]

\[\Rightarrow \hspace{0.3cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha}\hspace{0.05cm}.\]

Hierbei bezeichnet p_S = p_B(n = 1) die mittlere Symbolfehlerwahrscheinlichkeit und die empirisch gefundenen Werte von α liegen zwischen 0.5 und 0.95. Für 1 – α wird auch die Bezeichnung Bündelungsfaktor verwendet.

: Für das BSC–Modell gilt für den Verlauf der Blockfehlerwahrscheinlichkeit:

\[p_{\rm B}(n) =1 -(1 -p_{\rm S})^n \approx n \cdot p_{\rm S}\hspace{0.05cm}.\]

Daraus folgt α = 1 bzw. der Bündelungsfaktor 1 – α = 0. In diesem Fall (und nur in diesem) ergibt sich auch bei nicht–logarithmischer Darstellung ein linearer Verlauf.

Es ist aber zu beachten, dass obige Näherung nur für p_S << 1 und nicht allzu großes n zulässig ist, da sonst die Näherung (1 – p_S)ⁿ ≈ 1 – n · p_S nicht anwendbar ist. Das heißt aber auch, dass die oben angegebene Gleichung auch nur für einen unteren Bereich (für n < n^∗ ) gilt. Ansonsten würde sich für n → ∞ eine unendlich große Blockfehlerwahrscheinlichkeit ergeben.

Für die aus Messungen empirisch bestimmte Funktion p_B(n) muss nun die Fehlerabstandsverteilung gefunden werden, aus der der Verlauf für n > n^∗ extrapoliert werden kann und der die Nebenbedingung

\[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_{\rm B}(n) = 1 \]

erfüllt. Wir bezeichnen diesen Ansatz als das Wilhelm–Modell. Da das Gedächtnis nur bis zum letzten Symbolfehler reicht, wird dieses ein Erneuerungsmodell (englisch: Renewal Model) sein.

Fehlerabstandsbetrachtung zum Wilhelm–Modell (1)

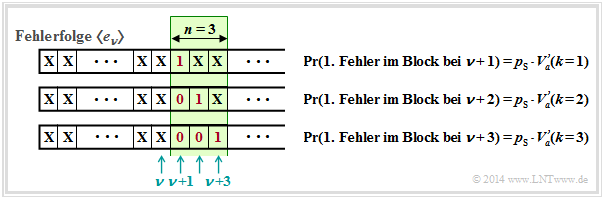
Betrachten wir nun die Fehlerabstände. Eine Fehlerfolge 〈e_ν〉 kann in äquivalenter Weise durch die Fehlerabstandsfolge 〈a_ν'〉 dargestellt werden, wie in der folgenden Grafik gezeigt. Man erkennt:

• Die Fehlerfolge ...1001... wird durch den Fehlerabstand a = 3 ausgedrückt.
  
• Entsprechend bezeichnet der Fehlerabstand a = 1 die Fehlerfolge ...11... .
  
• Die verschiedenen Indizes ν und ν' berücksichtigen, dass die beiden Folgen nicht synchron laufen.

Fehlerfolge und Fehlerabstandsfolge

Mit den Wahrscheinlichkeiten p_a(k) = Pr(a = k) für die einzelnen Fehlerabstände k und der mittleren (Bit–)Fehlerwahrscheinlichkeit p_S gelten folgende Definitionen für

• die Fehlerabstandsverteilung (FAV):             den mittleren Fehlerabstand E[a]:

\[ V_a(k) = {\rm Pr}(a \ge k)= \sum_{\kappa = k}^{\infty}p_a(\kappa) \hspace{0.05cm}, \hspace{0.93cm} {\rm E}[a] = \sum_{k = 1}^{\infty} k \cdot p_a(k) = {1}/{p_{\rm S}}\hspace{0.05cm}.\]

Wir betrachten nun einen Block mit n Bit, beginnend bei der Bitposition ν + 1. Ein Blockfehler tritt immer dann auf, wenn ein Bit an den Positionen ν + 1, ... , ν + n verfälscht ist.

Die Verfälschungswahrscheinlichkeiten werden in der Grafik durch die Fehlerabstandsverteilung V_a'(k) ausgedrückt. Irgendwo vor dem Block der Länge n = 3 befindet sich der letzte Fehler, aber mindestens im Abstand k vom ersten Fehler im Block entfernt. Also ist der Abstand gleich oder größer als k, was genau der Wahrscheinlichkeit V_a'(k) entspricht.

Hinweis. Das Hochkomma soll anzeigen, dass wir später noch eine Korrektur vornehmen müssen, um von der empirisch gefundenen FAV zur richtigen Funktion V_a(k) zu kommen.

Für die Blockfehlerwahrscheinlichkeit haben wir nun zwei Gleichungen: Durch Verallgemeinerung des obigen Bildes ergibt sich Gleichung (1). Die zweite Gleichung liefert unsere empirische Untersuchung:

\[(1)\hspace{0.2cm} p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) \hspace{0.05cm}, \hspace{0.4cm}(2)\hspace{0.2cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. \]

Fehlerabstandsbetrachtung zum Wilhelm–Modell (2)

Wir betrachten weiterhin die Blockfehlerwahrscheinlichkeit p_B(n) für einen Block mit n Bit:

\[(1)\hspace{0.2cm} p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) \hspace{0.05cm}, \hspace{0.4cm}(2)\hspace{0.2cm} p_{\rm B}(n) = p_{\rm S} \cdot n^{\alpha} \hspace{0.4cm}\Rightarrow\hspace{0.4cm} \sum_{k = 1}^{n} V_a\hspace{0.05cm}'(k) = n^{\alpha} \hspace{0.05cm}. \]

• Die Gleichung (1) wurde auf der letzten Seite hergeleitet. Sie stellt den Zusammenhang zwischen Blockfehlerwahrscheinlichkeit p_B(n) und (approximativer) Fehlerabstandsverteilung V_a′(k) her.
  

• Die Gleichung (2) lieferte unsere empirische Untersuchung zu Beginn dieses Abschnitts.
  

• Die letzte Gleichung ergibt sich aus Gleichsetzen von (1) und (2).
  
  

Durch sukzessives Einsetzen von n = 1, 2, 3, ... in diese Gleichung erhalten wir mit V_a'(1) = 1:

\[V_a\hspace{0.05cm}'(1) = 1^{\alpha} \hspace{0.05cm},\hspace{1.1cm} V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) =2^{\alpha} \hspace{0.05cm},\] \[V_a\hspace{0.05cm}'(1) + V_a\hspace{0.05cm}'(2) + V_a\hspace{0.05cm}'(3) = 3^{\alpha} \hspace{0.35cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}'(k) = k^{\alpha}-(k-1)^{\alpha} \hspace{0.05cm}.\]

Die aus empirischen Daten gewonnenen Koeffizienten V_a′(k) erfüllen jedoch nicht notwendigerweise die Normierungsbedingung. Um den Sachverhalt zu korrigieren, verwendet Wilhelm folgenden Ansatz:

\[V_a\hspace{0.05cm}(k) = V_a\hspace{0.05cm}'(k) \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} V_a\hspace{0.05cm}(k) = [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)}\hspace{0.05cm}.\]

Wilhelm bezeichnet diese Darstellung als L–Modell, siehe [Wil11]. Die Konstante β ist in Abhängigkeit

• der Symbolfehlerwahrscheinlichkeit p_S, und
  
• des empirisch gefundenen Exponenten α   ⇒   Bündelungsfaktor 1 – α
  
  

so zu bestimmen, dass die Blockfehlerwahrscheinlichkeit bei unendlich großer Blocklänge gleich 1 wird:

\[\lim_{n \hspace{0.05cm} \rightarrow \hspace{0.05cm} \infty} p_B(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) = p_{\rm S} \cdot \sum_{k = 1}^{n} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} =1 \hspace{0.05cm}\]

\[\Rightarrow \hspace{0.3cm} \sum_{k = 1}^{\infty} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} = {1}/{p_{\rm S}} \hspace{0.05cm}.\]

Um β zu bestimmen, wird die erzeugende Funktion von V_a(k) verwendet, die wir mit V_a(z) benennen:

\[V_a\hspace{0.05cm}(z) = \sum_{k = 1}^{\infty}V_a\hspace{0.05cm}(k) \cdot z^k = \sum_{k = 1}^{n} [k^{\alpha}-(k-1)^{\alpha} ] \cdot {\rm e}^{- \beta \cdot (k-1)} \cdot z^k \hspace{0.05cm}.\]

In [Wil11] wird näherungsweise hergeleitet:

\[V_a\hspace{0.05cm}(z) = \frac{1}{\left (1- {\rm e}^{- \beta }\cdot z \right )^\alpha} \hspace{0.05cm}.\]

Aus der Gleichung für den mittleren Fehlerabstand folgt:

\[ {\rm E}[a] = \sum_{k = 1}^{\infty} k \cdot p_a(k) ='"`UNIQ--h-10--QINU`"' \sum_{k = 1}^{\infty} V_a(k) = \sum_{k = 1}^{\infty} V_a(k) \cdot 1^k = V_a(z=1) = {1}/{p_{\rm S}}\hspace{0.05cm}\]

\[\Rightarrow \hspace{0.3cm}{p_{\rm S}} = \left [V_a(z=1)\right]^{-1}= \left [1- {\rm e}^{- \beta }\cdot 1\right]^{\alpha} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm e}^{- \beta } =1 - {p_{\rm S}}^{1/\alpha}\hspace{0.05cm}.\]

Numerischer Vergleich von BSC–Modell und Wilhelm–Modell (1)

Fassen wir dieses Zwischenergebnis zusammen, das von Wilhelm als L–Modell bezeichnet wird.

Das L–Modell nach Wilhelm beschreibt die Fehlerabstandsverteilung in der Form

\[V_a\hspace{0.05cm}(k) = \left [k^{\alpha}-(k-1)^{\alpha}\right ] \cdot \left [ 1 - {p_{\rm S}^{1/\alpha}}\right ]^{k-1} \hspace{0.05cm}.\]

Dieses Modell soll nun anhand beispielhafter numerischer Ergebnisse erläutert werden.

1 : Wir gehen zunächst vom BSC–Modell aus. Die Verfälschungswahrscheinlichkeit setzen wir aus Darstellungsgründen sehr hoch auf p_S = 0.2. In der zweiten Zeile der nachfolgenden Tabelle ist dessen Fehlerabstandsverteilung V_a(k) = Pr(a ≥ k) für k ≤ 10 eingetragen.

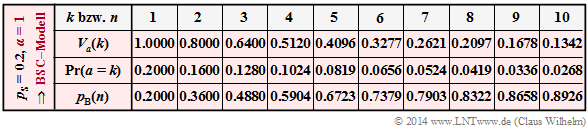
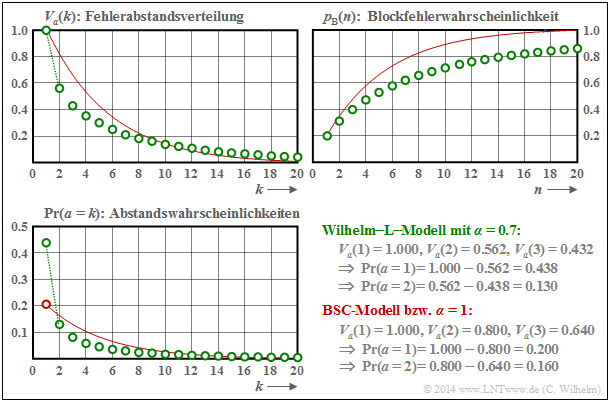
Das Wilhelm–Modell mit p_S = 0.2 und α = 1 weist genau die gleiche Fehlerabstandsverteilung V_a(k) wie das entsprechende BSC–Modell auf. Dies zeigt auch die Rechnung. Mit α = 1 erhält man aus der Gleichung auf der letzten Seite:

\[V_a\hspace{0.05cm}(k) = \left [k^{\alpha}-(k-1)^{\alpha}\right ] \cdot \left [ 1 - {p_{\rm S}^{1/\alpha}}\right ]^{k-1} = (1 - p_{\rm S})^{k-1} \hspace{0.05cm}.\]

Damit besitzen beide Modelle entsprechend den Zeilen 3 und 4 auch

• gleiche Wahrscheinlichkeiten Pr(a = k) = V_a(k–1) – V_a(k) der Fehlerabstände,
  

• gleiche Blockfehlerwahrscheinlichkeiten p_B(n).
  
  

Im Hinblick auf das folgende Beispiel mit α ≠ 1 ist nochmals besonders zu erwähnen:

• Die Blockfehlerwahrscheinlichkeiten p_B(n) des Wilhelm–Modells ergeben sich grundsätzlich aus der Fehlerabstandsverteilung V_a(k) entsprechend der Gleichung

\[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} V_a\hspace{0.05cm}(k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \cdot 1 = 0.2 \hspace{0.05cm}, \hspace{0.15cm}p_{\rm B}(2) = 0.2 \cdot (1+0.8) = 0.36 \hspace{0.05cm}.\]

• Im Sonderfall α = 1  ⇒  BSC–Modell (und nur in diesem) kann p_B(n) auch durch Summation über die Fehlerabstandswahrscheinlichkeiten Pr(a = k) ermittelt werden:

\[ p_{\rm B}(n) = p_{\rm S} \cdot \sum_{k = 1}^{n} {\rm Pr}(a=k) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} p_{\rm B}( 1) = 0.2 \hspace{0.05cm}, \hspace{0.15cm}p_{\rm B}(2) = 0.2+ 0.16 = 0.36 \hspace{0.05cm}.\]

Numerischer Vergleich von BSC–Modell und Wilhelm–Modell (2)

2 : Betrachten wir nun einen Kanal mit Bündelfehlercharakteristik. Die Grafik zeigt als grüne Kreise die Ergebnisse für das Wilhelm–L–Modell mit α = 0.7. Die rote Vergleichskurve gilt für α = 1 (bzw. für den BSC–Kanal) bei gleicher mittlerer Symbolfehlerwahrscheinlichkeit p_S = 0.2. Unten rechts sind einige interessante Zahlenwerte angegeben.

Man erkennt aus diesen Darstellungen:

• Der Verlauf der Blockfehlerfehlerwahrscheinlichkeit beginnt jeweils mit p_B(n = 1) = p_S = 0.2, sowohl bei statistisch unabhängigen Fehlern (BSC) als auch bei Bündelfehlern (Wilhelm).
  

• Beim Bündelfehlerkanal ist Pr(a = 1) = 0.438 deutlich größer als beim vergleichbaren BSC ⇒ Pr(a = 1) = 0.2. Zudem erkennt man einen abgeknickten Verlauf im unteren Bereich.
  

• Der mittlere Fehlerabstand E[a] = 1/p_S = 5 ist aber bei gleicher Symbolfehlerwahrscheinlichkeit ebenfalls identisch. Der große Ausreiser bei k = 1 wird durch kleinere Wahrscheinlichkeiten für k = 2, k = 3 und k = 4 ausgeglichen, sowie durch die Tatsache, dass für große k die grünen Kreise – wenn auch nur minimal – oberhalb der roten Vergleichskurve liegen.
  

• Das wichtigste Ergebnis ist aber, dass die Blockfehlerfehlerwahrscheinlichkeit für n > 1 beim Bündelfehlerkanal kleiner ist als beim vergleichbaren BSC–Modell, z.B.:  p_B(n = 20) = 0.859.

Bevor wir dieses interessante Ergebnis interpretieren, beschreiben wie zunächst die endgültige Variante des Kanalmodells nach Wilhelm. Wir nennen es das Wilhelm–A–Modell.

Fehlerabstandsbetrachtung nach dem Wilhelm–A–Modell

Wilhelm hat aus der angegebenen erzeugenden Funktion V_a(z) eine weitere Näherung entwickelt, die er als das A–Modell bezeichnet. Die Näherung basiert auf einer Taylorreihenentwicklung.

Das A–Modell nach Wilhelm beschreibt die angenäherte Fehlerabstandsverteilung in der Form

\[V_a\hspace{0.05cm}(k) = \frac {1 \cdot \alpha \cdot (1+\alpha) \cdot \hspace{0.05cm} ... \hspace{0.05cm}\cdot (k-2+\alpha) }{(k-1)\hspace{0.05cm}!}\cdot \left [ 1 - {p_{\rm S}^{1/\alpha}}\right ]^{k-1} \hspace{0.05cm}.\]

Insbesondere ergibt sich V_a(k = 1) = 1 und V_a(k = 2) = α · (1 – p_S^1/α). Hierbei ist zu berücksichtigen, dass der Zähler des Vorfaktors aus k Faktoren besteht. Für k = 1 ergibt sich dieser demzufolge zu 1.

Im nachfolgenden Beispiel vergleichen wir die Unterschiede der beiden Wilhelm–Modelle (L bzw. A) hinsichtlich der resultierenden Blockfehlerwahrscheinlichkeit.

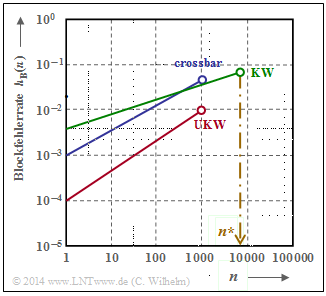
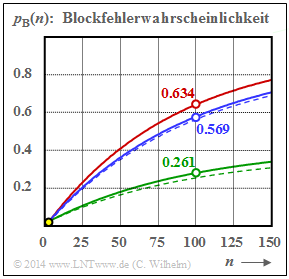3 : Nebenstehende Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeiten p_B(n) für drei verschiedene α–Werte, erkennbar an den Farben

• Rot:   α = 1  ⇒  BSC–Modell,
  

• Blau:  α = 0.95  ⇒  schwache Bündelung,
  

• Grün:  α = 0.70  ⇒  starke Bündelung.
  
  

Die durchgezogennen gelten für Linien das A–Modell und die gestrichelten für das L–Modell. Die im Bild angegebenen Zahlenwerte für p_B(n = 100) beziehen sich ebenfalls auf das A–Modell.

Für α = 1 geht sowohl das A–Modell als auch das L–Modell in das BSC–Modell (rote Kurve) über. Desweiteren ist anzumerken:

• Die Symbolfehlerwahrscheinlichkeit p_S = 0.01  ⇒  E[a = 100] ist hier (einigermaßen) realistisch angenommen. Alle Kurven starten deshalb bei p_B(n = 1) = 0.01  ⇒  gelbe Markierung.
  

• Der Unterschied zwischen zwei gleichfarbigen Kurven ist gering (bei starker Bündelung etwas größer), wobei die durchgezogene Kurve stets oberhalb der gestrichelten Kurve liegt.
  

• Auch dieses Beispiel zeigt: Je stärker die Bündelung (kleineres α), desto kleiner ist p_B(n). Dies gilt allerdings nur, wenn man wie hier von einer konstanten Fehlerwahrscheinlichkeit p_S ausgeht.
  

• Ein (dürftiger) Erklärungsversuch: Nehmen wir an, dass bei BSC mit sehr kleinem p_S jeder Blockfehler von genau einem Symbolfehler herrührt, dann wird bei gleicher Symbolfehleranzahl die Anzahl der Blockfehler kleiner, wenn zwei Symbolfehler in einen Block fallen (Bündelung).
  

• Noch ein (passendes?) Beispiel aus dem täglichen Leben. Man kann eine Straße mit konstantem Verkehrsaufkommen leichter überqueren, wenn die Fahrzeuge „irgendwie gebündelt” kommen.

Fehlerkorrelationsfunktion des Wilhelm–Modells

Eine weitere Beschreibungsform der digitalen Kanalmodelle neben der Fehlerabstandsverteilung V_a(k) ist die Fehlerkorrelationsfunktion φ_e(k) – abgekürzt FKF. Geht man von der binären Fehlerfolge 〈e_ν〉 mit e_ν ∈ {0, 1} aus, wobei e_ν = 0 eine richtige Übertragung und e_ν = 1 einen Symbolfehler (Bitfehler) hinsichtlich des ν–ten Bits bezeichnet, so gilt folgende Definition:

\[\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] = \overline{e_{\nu} \cdot e_{\nu + k}}\hspace{0.05cm}.\]

φ_e(k) gibt die (zeitdiskrete) Autokorrelationsfunktion der ebenfalls zeitdiskreten Zufallsgröße e an. Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.

Der Fehlerkorrelationswert φ_e(k) liefert statistische Aussagen bezüglich zwei um k auseinander liegende Folgenelemente, zum Beispiel über e_ν und e_ν+k. Die dazwischen liegenden Elemente e_ν+1, ... , e_ν+k–1 beeinflussen den φ_e(k)–Wert nicht.

Die Fehlerkorrelationsfunktion des Wilhelm–Modells kann wie folgt angenähert werden:

\[\varphi_e\hspace{0.05cm}(k) = p_{\rm S} \hspace{-0.03cm}\cdot \hspace{-0.03cm} \left [ 1 \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha}{1\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C \hspace{-0.03cm}-\hspace{-0.03cm} \frac{\alpha \cdot (1\hspace{-0.03cm}-\hspace{-0.03cm} \alpha)}{2\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^2 \hspace{-0.03cm}-\hspace{-0.03cm} \hspace{0.03cm} ... \hspace{0.03cm}\hspace{-0.03cm}-\hspace{-0.03cm} \frac {\alpha \hspace{-0.03cm}\cdot \hspace{-0.03cm} (1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) \hspace{-0.03cm}\cdot \hspace{-0.03cm} \hspace{0.03cm} ... \hspace{0.03cm} \hspace{-0.03cm}\cdot \hspace{-0.03cm} (k\hspace{-0.03cm}-\hspace{-0.03cm}1\hspace{-0.03cm}-\hspace{-0.03cm}\alpha) }{k\hspace{0.03cm}!} \hspace{-0.03cm}\cdot \hspace{-0.03cm} C^k \right ] \]

Zur Abkürzung ist hierbei C= 1 – p_S^1/α verwendet. Auf die Herleitung wird hier verzichtet.

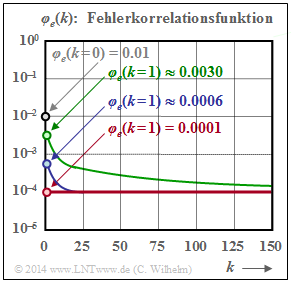
Nachfolgend werden die Eigenschaften der Fehlerkorrelationsfunktion an einem Beispiel aufgezeigt.

3:

Wie im Beispiel 2 gelte p_S = 0.01. Die hier dargestellten Fehlerkorrelationsfunktionen stehen wieder für

• α = 0.7 (grüne Kurve),
  

• α = 0.95 (blaue Kurve) und
  

• α = 1 (BSC, rote Kurve).
  
  

Die nachfolgenden Aussagen lassen sich weitgehend verallgemeinern, siehe auch GE–Modell:

• Der FKF-Wert an der Stelle k = 0 ist bei allen Kanälen gleich p_S = 0.01 (markiert durch den Kreis mit grauer Füllung) und der Grenzwert für k → ∞ liegt stets bei p_S² = 0.0001.
  

• Dieser Endwert wird beim BSC–Modell bereits bei k = 1 erreicht (rot gefüllte Markierung). Hier kann die FKF also nur die beiden Werte p_S und p_S² annehmen.
  

• Auch für für α ≠ 1 erkennt man einen Knick bei k = 1. Danach verläuft die FKF monoton fallend. Der Abfall ist umso langsamer, je kleiner α ist, also je gebündelter die Fehler auftreten.

Analyse von Fehlerstrukturen mit dem Wilhelm–Modell (1)

Wilhelm hat sein Kanalmodell hauptsächlich deshalb entwickelt, um aus gemessenen Fehlerfolgen Rückschlüsse über die dabei auftretenden Fehler machen zu können. Aus der Vielzahl der Analysen in [Wil11] sollen hier nur einige wenige angeführt werden, wobei stets die Symbolfehlerwahrscheinlichkeit p_S = 0.001 zugrunde liegt. In den Grafiken gilt jeweils die rote Kurve für statistisch unabhängige Fehler (BSC bzw. α = 1) und die grüne Kurve für einen Bündelfehlerkanal mit α = 0.7. Zudem soll gelten:

: Ein Fehlerburst (oder kurz Burst) beginnt stets mit einem Symbolfehler und endet, wenn k_Burst – 1 fehlerfreie Symbole aufeinanderfolgen; k_Burst bezeichnet den Burst–Endeparameter. Das Burstgewicht G_Burst entspricht der Anzahl aller Symbolfehler im Burst. Bei einem Einzelfehler gilt G_Burst = 1 und die Burstlänge L_Burst (bestimmt durch den ersten und letzten Fehler) ist ebenfalls 1.

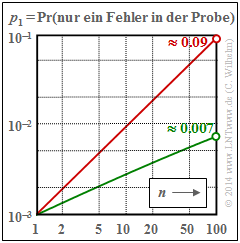
Wahrscheinlichkeit eines Einzelfehlers in einer Probe der Länge n   ⇒   p₁

Für den BSC–Kanal (α = 1) gilt p₁ = n · 0.001 · 0.999^n–1  ⇒  rote Kurve. Aufgrund der doppel–logarithmischen Darstellung ergibt sich mit diesen Zahlenwerten ein (nahezu) linearer Verlauf. Beim BSC–Modell treten also Einzelfehler in einer Probe der Länge n = 100 mit etwa 9% Wahrscheinlichkeit auf.

Beim Bündelfehlerkanal mit α = 0.7 (grüne Kurve) beträgt die entsprechende Wahrscheinlichkeit nur etwa 0.7% und der Kurvenverlauf ist hier leicht gekrümmt. Bei der folgenden Rechnung gehen wir zunächst von der Annahme aus, dass der Einzelfehler in der Probe der Länge n an Position b auftritt:

• Bei einem Einzelfehler müssen dann noch n – b fehlerfreie Symbole folgen. Nach Mittelung über die möglichen Fehlerpositionen b erhält man somit:

\[p_1 = p_{\rm S} \cdot \sum_{b = 1}^{n} \hspace{0.15cm}V_a (b) \cdot V_a (n+1-b) \hspace{0.05cm}.\]

• Wegen der Ähnlichkeit mit der Signaldarstellung eines Digitalen Filters kann man die Summe als Faltung von V_a(b) mit sich selbst bezeichnen. Für die erzeugende Funktion V_a(z) wird aus der Faltung ein Produkt (bzw. wegen V_a(b) ∗ V_a(b) das Quadrat) und man erhält folgende Gleichung:

\[V_a(z=1) \cdot V_a(z=1) = \left [ V_a(z=1) \right ]^2 = {\left [ 1 -(1- {p_{\rm S}}^{1/\alpha})\right ]^{-2\alpha}} \hspace{0.05cm}.\]

• Mit der spezifischen Fehlerabstandsverteilung V_a(z) erhält man somit folgendes Endergebnis:

\[p_1 = p_{\rm S} \cdot \frac{2\alpha \cdot (2\alpha+1) \cdot \hspace{0.05cm} ... \hspace{0.05cm} \cdot (2\alpha+n-2)} {(n-1)!}\cdot (1- {p_{\rm S}}^{1/\alpha})^{n-1} \hspace{0.05cm}.\]

Analyse von Fehlerstrukturen mit dem Wilhelm–Modell (2)

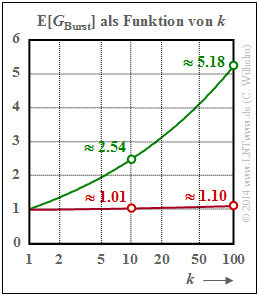
Mittlere Fehleranzahl in einem Burst mit dem Burst–Endeparameter k_Burst   ⇒   E[G_Burst]

Die mittlere Symbolfehlerwahrscheinlichkeit wird weiterhin mit p_S = 0.001 als (relativ) klein angenommen.

1. Rote Kurve für den BSC–Kanal (bzw. α = 1):
   • Der Parameter k_Burst = 10 bedeutet beispielsweise, dass der Burst beendet ist, wenn nach einem Fehler neun fehlerfreie Symbole aufeinanderfolgenden. Die Wahrscheinlichkeit für einen Fehlerabstand a ≤ 9 ist bei kleinem p_S (hier: 0.001) äußerst klein. Daraus folgt weiter, dass dann (fast) jeder Einzelfehler als ein „Burst” aufgefasst wird, und es gilt E[G_Burst] ≈ 1.01.
     
   • Bei größerem Burst–Endeparameter nimmt auch die Wahrscheinlichkeit Pr(a ≤ k_Burst) deutlich zu und es kommt zu „Bursts” mit mehr als einem Fehler. Wählt man beispielsweise k_Burst = 100, so beinhaltet ein „Burst” im Mittel 1.1 Symbolfehler.
     
   • Das bedeutet gleichzeitig, dass es auch beim BSC–Modell zu langen Fehlerbursts (entsprechend unserer Definition) kommen kann, wenn bei gegebenem p_S der Burst–Endeparameter zu groß gewählt ist oder bei vorgegebenem k_Burst die mittlere Fehlerwahrscheinlichkeit p_S zu groß ist.
     
     
2. Grüne Kurve für den Wilhelm–Kanal mit α = 0.7:

   Das hier angegebene Verfahren zur numerischen Bestimmung der mittleren Fehleranzahl E[G_Burst] eines Bursts kann unabhängig vom α–Wert angewendet werden. Man geht wie folgt vor:

   • Entsprechend den Fehlerabstandswahrscheinlichkeiten Pr(a = k) generiert man eine Fehlerfolge e₁, e₂, ... , e_i, ... mit den Fehlerabständen a₁, a₂, ... , a_i, ...
     
   • Ist ein Fehlerabstand a_i ≥ k_Burst, so kennzeichnet dieser das Ende eines Bursts. Ein solches Ereignis tritt mit der Wahrscheinlichkeit Pr(a ≥ k_Burst) = V_a(k_Burst) ein.
     
   • Wir zählen solche Ereignisse „a_i ≥ k_Burst” im gesamten Block der Länge n. Deren Anzahl ist gleichzeitig die Anzahl der Burst im Block. Wir bezeichnen diese Anzahl mit N_Burst.
     
   • Gleichzeitig gilt die Beziehung N_Burst = N_Fehler · V_a(k_Burst), wobei N_Fehler die Anzahl aller Fehler im Block angibt. Daraus lässt sich die mittlere Fehlerzahl pro Burst in einfacher Weise berechnen:

\[{\rm E}[G_{\rm Burst}] =\frac {N_{\rm Fehler}}{N_{\rm Burst}} =\frac {1}{V_a(k_{\rm Burst})}\hspace{0.05cm}.\]

Die Marker in der Grafik korrespondieren mit folgenden Zahlenwerten der Fehlerabstandsverteilung. Die grünen Kreise (Wilhelm–Kanal, α = 0.7) ergeben sich aus V_a(10) = 0.394 und V_a(100) = 0.193, die roten Kreise (BSC–Kanal, α = 1) sind die Kehrwerte von V_a(10) = 0.991 und V_a(100) = 0906.

Aufgaben

A5.6 Fehlerkorrelationsdauer

Zusatzaufgaben:5.6 GE-Modelleigenschaften

A5.7 MC- aus GE-Parameter

Zusatzaufgaben:5.7 Nochmals MC-Modell