Exercise 3.10: Maximum Likelihood Tree Diagram

Signale und Baumdiagramm

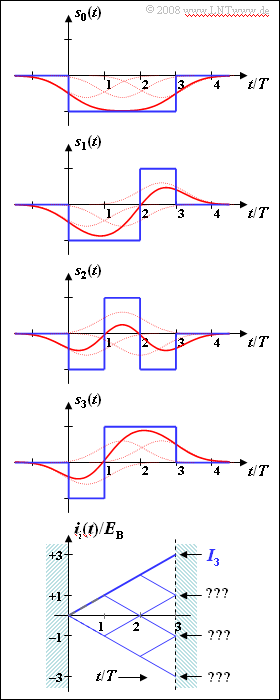
Wie in Aufgabe 3.9 betrachten wir die gemeinsame Entscheidung dreier Binärsymbole (Bits) mittels des Korrelationsempfängers. Die möglichen Sendesignale $s_0(t), \ \text{...} \ , \ s_7(t)$ seien bipolar. In der Grafik sind die Funktionen $s_0(t)$, $s_1(t)$, $s_2(t)$ und $s_3(t)$ dargestellt. Die blauen Kurvenverläufe gelten dabei für rechteckförmige NRZ–Sendeimpulse.

Darunter gezeichnet ist das so genannte Baumdiagramm für diese Konstellation unter der Voraussetzung, dass das Signal $s_3(t)$ gesendet wurde. Dargestellt sind hier im Bereich von $0$ bis $3T$ die Funktionen

$$i_i(t) = \int_{0}^{t} s_3(\tau) \cdot s_i(\tau) \,{\rm d} \tau \hspace{0.3cm}( i = 0, \ \text{...} \ , 7)\hspace{0.05cm}.$$

Der Korrelationsempfänger vergleicht die Endwerte $I_i = i_i(3T)$ miteinander und sucht den größtmöglichen Wert $I_j$.
Das zugehörige Signal $s_j(t)$ ist dann dasjenige, das gemäß dem Maximum–Likelihood–Kriterium am wahrscheinlichsten gesendet wurde.

Anzumerken ist, dass der Korrelationsempfänger im allgemeinen die Entscheidung anhand der korrigierten Größen $W_i = I_i \ – E_i/2$ trifft. Da aber bei bipolaren Rechtecken alle Sendesignale ($i = 0, \ \text{...} \ , \ 7$) die genau gleiche Energie

$$E_i = \int_{0}^{3T} s_i^2(t) \,{\rm d} t$$

aufweisen, liefern die Integrale $I_i$ genau die gleichen Maximum–Likelihood–Informationen wie die korrigierten Größen $W_i$.

Die roten Signalverläufe $s_i(t)$ ergeben sich aus den blauen durch Faltung mit der Impulsantwort $h_{\rm G}(t)$ eines Gaußtiefpasses mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.35$.

Jeder einzelne Rechteckimpuls wird verbreitert.
Die roten Signalverläufe führen bei Schwellenwertentscheidung zu Impulsinterferenzen.

Hinweise:

Die Aufgabe gehört zum Kapitel Optimale Empfängerstrategien.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$I_0/E_{\rm B} \ = \ $

$I_2/E_{\rm B} \ = \ $

$I_4/E_{\rm B} \ = \ $

$I_6/E_{\rm B} \ = \ $

	Das Baumdiagramm ist weiter durch Geradenstücke beschreibbar.
	Ist $I_3$ der maximale $I_i$–Wert, so entscheidet der Empfänger richtig.
	Es gilt unabhängig von der Stärke der Störungen $I_0 = I_6$.

	Das Baumdiagramm ist weiter durch Geradenstücke beschreibbar.
	Die Signalenergien $E_i(i = 0, \ \text{...} \ , 7$) sind unterschiedlich.
	Es sind sowohl die Entscheidungsgrößen $I_i$ als auch $W_i$ geeignet.

	Ohne Impulsinterferenzen (blau) sind $t_1 = 0$ und $t_2 = 3T$ bestmöglich.
	Mit Impulsinterferenzen (rot) sind $t_1 = 0$ und $t_2 = 3T$ bestmöglich.

Musterlösung

Solution

(1) Die linke Grafik zeigt das Baumdiagramm (ohne Rauschen) mit allen Endwerten. Grün hervorgehoben ist der Verlauf $i_0(t)/E_{\rm B}$ mit dem Endergebnis $I_0/E_{\rm B} = \ –1$, der zunächst linear bis $+1$ ansteigt – das jeweils erste Bit von $s_0(t)$ und $s_3(t)$ stimmen überein – und dann über zwei Bitdauern abfällt.

Baumdiagramm des Korrelationsempfängers

Die richtigen Ergebnisse lauten somit:

$$I_0/E_{\rm B}\hspace{0.15cm}\underline { = -1}, \hspace{0.2cm}I_2/E_{\rm B} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}I_4/E_{\rm B} \hspace{0.15cm}\underline {= -3}, \hspace{0.2cm}I_6/E_{\rm B}\hspace{0.15cm}\underline { = -1} \hspace{0.05cm}.$$

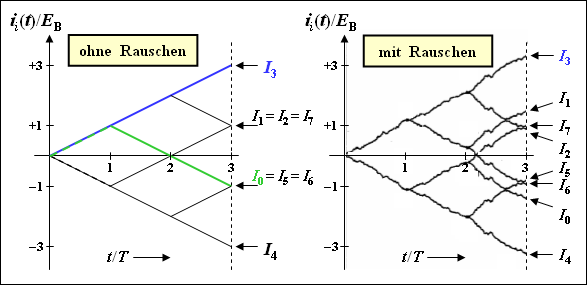
(2) Bei Vorhandensein von (Rausch–) Störungen nehmen die Funktionen $i_i(t)$ nicht mehr linear zu bzw. ab, sondern haben einen Verlauf wie in der oberen Grafik dargestellt. Solange $I_3 > I_{\it i≠3}$ ist, entscheidet der Korrelationsempfänger richtig. Bei Vorhandensein von Störungen gilt stets $I_0 ≠ I_6$ im Gegensatz zum störungsfreien Baumdiagramm. Richtig ist also nur der zweite Lösungsvorschlag.

(3) Auch hier ist nur die zweite Aussage zutreffend. Da nun die möglichen Sendesignale $s_i(t)$ nicht mehr aus horizontalen Abschnitten zusammengesetzt werden können, besteht auch das Baumdiagramm ohne Störungen nicht aus Geradenstücken. Da die Energien $E_i$ unterschiedlich sind – dies erkennt man zum Beispiel durch den Vergleich der Signale $s_0(t)$ und $s_2(t)$ – müssen für die Entscheidung unbedingt die korrigierten Größen $W_i$ herangezogen werden. Die Verwendung der reinen Korrelationswerte $I_i$ kann bereits ohne Störungen zu Fehlentscheidungen führen.

(4) Im Fall ohne Impulsinterferenzen (blaue Rechtecksignale) sind alle Signale auf den Bereich $0 \ ... \ 3T$ begrenzt. Außerhalb stellt das Empfangssignal $r(t)$ reines Rauschen dar. Deshalb genügt in diesem Fall auch die Integration über den Bereich $0 \ ... \ 3T$. Richtig ist Antwort 1.

Demgegenüber unterscheiden sich bei Berücksichtigung von Impulsinterferenzen (rote Signale) die Integranden $s_3(t) \cdot s_i(t)$ auch außerhalb dieses Bereichs. Wählt man $t_1 = \ –T$ und $t_2 = +4T$, so wird deshalb die Fehlerwahrscheinlichkeit des Korrelationsempfängers gegenüber dem Integrationsbereich $0 \ ... \ 3T$ weiter verringert.