Exercise 4.2Z: Eight-level Phase Shift Keying

• Return to book

Signalraumpunkte bei 8-PSK

Die $M = 8$ möglichen Sendesignale bei 8–PSK lauten mit $i = 0, \ ... \ , 7$ im Bereich $0 ≤ t < T$:

$$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$

Außerhalb der Symboldauer $T$ sind die Signale $s_i(t)$ alle gleich $0$.

In der Aufgabe A4.2 wurde gezeigt, dass diese Signalmenge durch die Basisfunktionen

$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$

$$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$

wie folgt dargestellt werden kann ($i = 0, \ ... \ , 7$):

$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$

Die äquivalente Tiefpassdarstellung der Signale $s_i(t)$ lautet nach dem Blockschaltbild in Kapitel 4.3 des Buches „Modulationsverfahren”:

$$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} \hspace{0.05cm}, \hspace{0.2cm}i = 0, ... \hspace{0.1cm} , 7 \hspace{0.05cm},$$

wobei $a_i$ komplexe dimensionslose Koeffizienten sind und die Energie des Sendegrundimpulses $g_s(t)$ im Tiefpassbereich $E_{\it gs}$ beträgt. Im hier dargestellten Fall beschreibt $g_s(t)$ einen Rechteckimpuls, doch kann für $g_s(t)$ auch ein jeder andere energiebegrenzte Impuls verwendet werden.

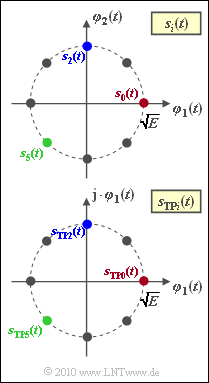
Die Grafik zeigt die Signalraumdarstellung der 8–PSK für das Bandpass–Signal (oben) sowie für das äquivalente Tiefpass–Signal (unten). Man erkennt daraus, dass sich die beiden Darstellungen nur duch die verwendeten Basisfunktionen unterscheiden, wobei $\varphi_1(t)$ in der oberen und der unteren Grafik für unterschiedliche Funktionen steht. In der Tiefpassdarstellung gilt $\varphi_2(t) = j \cdot \varphi_1(t)$.

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Kapitel Signale, Basisfunktionen und Vektorräume.
• Im Gegensatz zum Theorieteil und zur Aufgabe A4.2 kann hier die Laufvariable $i$ die Werte $0, \ ... \, M–1$ annehmen. Verwenden Sie zur Abkürzung

$$E = {A^2 \cdot T}/{2}\hspace{0.05cm}.$$

Fragebogen

1

Wie lauten die Koeffizienten des Signals $s_0(t)$?

$s_{\rm 01}$ = $\ \cdot E^{\rm 0.5}$

$s_{\rm 02}$ = $\ \cdot E^{\rm 0.5}$

2

Wie lauten die Koeffizienten des Signals $s_2(t)$?

$s_{\rm 21}$ = $\ \cdot E^{\rm 0.5}$

$s_{\rm 22}$ = $\ \cdot E^{\rm 0.5}$

3

Wie lauten die Koeffizienten des Signals $s_5(t)$?

$s_{\rm 51}$ = $\ \cdot E^{\rm 0.5}$

$s_{\rm 52}$ = $\ \cdot E^{\rm 0.5}$

4

Durch welche Basisfunktionen sind die TP–Signale $s_{\rm TP \it i}(t) darstellbar? Durch

	eine komplexe Basisfunktion $\xi_1(t)$,
	zwei komplexe Basisfunktionen $\xi_1(t)$ und $\xi_2(t)$,
	zwei reelle Funktionen $\varphi_1(t)$ und $\psi_1(t)$.

5

Wie lauten im vorliegenden Fall die reellen Basisfunktionen?

	$\varphi_1(t) = g_s(t)$,
	$\varphi_1(t) = g_s(t)/E_{\rm gs}^{\rm 0.5}$,
	$\psi_1(t) = \varphi_1(t)$,
	$\psi_1(t) = j \cdot \varphi_1(t)$.

6

Es gelte $s_{\rm TP0}(t) = E^{\rm 0.5}$. Was trifft zu:

	Die Energie $E$ bezieht sich auf das Tiefpass–Signal.
	Die Energie $E$ bezieht sich auf das Bandpass–Signal.

Musterlösung

Solution

(1)  Es ist

$$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$

Da dieses Signal keinen Sinusteil aufweist, ist $s_{\rm 02} = 0$. Weiter gilt mit der angegebenen Abkürzung:

$$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$

(2)  Das Signal $s_2(t)$ lautet mit $i = 2$ (beachten Sie, dass die zweite Basisfunktion minus–sinusförmig ist):

$$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t )$$

$$\Rightarrow \hspace{0.3cm} s_{21}\hspace{0.05cm} \underline{= 0}\hspace{0.05cm}, \hspace{0.2cm} s_{22}= \sqrt{E} \hspace{0.05cm} \hspace{0.15cm}\underline {=1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$

(3)  Entsprechend den Musterlösungen zu (1) und (2) gilt nun:

$$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$

$$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )=$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t + \phi_5)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\phi_5 = -0.75 \cdot \pi \hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}\phi_5 = 1.25 \cdot \pi \hspace{0.05cm}.$$

(4)  Richtig sind die Lösungsvorschläge 1 und 3. Dabei gilt folgender Zusammenhang:

$$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$

(5)  Richtig sind hier die Alternativen 2 und 3. Die Basisfunktion muss energienormiert sein und $\psi_1(t)$ ist wie $\varphi_1(t)$ eine reelle, nicht etwa eine imaginäre Funktion:

$$\varphi_1 (t) = \psi_1 (t) = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$

(6)  Aus dem Tiefpass–Signal $s_{\rm TP0}(t)$ kann auch das Bandpass–Signal $s_0(t)$ berechnet werden. Im Bereich $0 ≤ t ≤ T$ gilt mit dem Ergebnis aus (5):

$$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] = {\rm Re}[\sqrt{E} \cdot \frac{1}{\sqrt{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ]=$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$

also das gleiche Ergebnis wie in der Teilaufgabe (1). Daraus folgt: Die Energie $E$ bezieht sich auch bei Betrachtung im äquivalenten Tiefpass–Bereich auf das Bandpass–Signal.

Entsprechend gilt für das mit blauem Punkt markierte Signal $s_2(t)$ im interessierenden Bereich:

$$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] = && :&& \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t)- \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) ] =$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \hspace{0.05cm}.$$

Schließlich kann für das (grüne) Signal $s_5(t)$ im Bereich $0 ≤ t < T$ geschrieben werden:

$$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] = ... =$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{\frac{E}{2T}} \cdot \cos(2\pi f_{\rm T}t)+ \sqrt{\frac{E}{2T}} \cdot \sin(2\pi f_{\rm T}t)=$$

$$\hspace{-0.1cm} \ = \ \hspace{-0.1cm}\sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t + 1.25 \cdot \pi) \hspace{0.05cm}.$$

Auch diese Ergebnisse stimmen mit denen der Teilaufgaben (2) bzw. (3) überein. Zutreffend ist also der Lösungsvorschlag 2.