Exercise 4.3: Different Frequencies

• Return to book

Vorgegebene Signalmenge

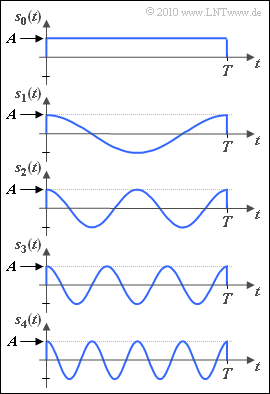
In der Grafik sind $M = 5$ Signale $s_i(t)$ dargestellt. Entgegen der Nomenklatur im Theorieteil sind für die Laufvariable $i$ die $0, \ ... \ , M–$ möglich. Anzumerken ist:

• Alle Signale sind zeitbegrenzt auf $0$ bis $T$; damit ist auch die Energie aller Signale endlich.
• Das Signal $s_1(t)$ hat die Periodendauer $T_0 = T$. Die Frequenz ist damit gleich $f_0 = 1/T$.
• Die Signale $s_i(t)$, $i ≠ 0$, sind Cosinusschwingungen mit der Frequenz $i \cdot f_0$. Dagegen ist $s_0(t)$ zwischen $0$ und $T$ konstant.
• Der Maximalwert aller Signale ist $A$ und es gilt $|s_i(t)| ≤ A$.

Gesucht sind in dieser Aufgabe die $N$ Basisfunktionen, die hier entgegen der bisherigen Beschreibung im Theorieteil mit $j = 0, \ ... \ , N–1$ durchnummeriert werden.

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel Signale, Basisfunktionen und Vektorräume.

Fragebogen

1

Beschreiben Sie die Signalmenge $\{s_i(t)\}, 0 ≤ i ≤ 4$ möglichst kompakt. Welche Beschreibungsform ist richtig?

	$s_i(t) = A \cdot \cos {2\pi i \cdot t/T}$.
	$s_i(t) = A \cdot \cos {2\pi i \cdot t/T}$ für $0 ≤ t < T$, sonst $0$.
	$s_i(t) = A \cdot \cos {2\pi i – i \cdot \pi/2}$ für $0 ≤ t < T$, sonst $0$.

2

Geben Sie die Anzahl $N$ der erforderlichen Basisfunktionen an.

$N$ =

3

Wie lautet die Basisfunktion $\varphi_0(t)$, die formgleich $s_0(t)$ ist?

	$\varphi_0(t) = s_0(t)$,
	$\varphi_0(t) = (1/T)^{\rm 0.5}$ für $0 ≤ t < T$, außerhalb $0$.
	$\varphi_0(t) = (2/T)^{\rm 0.5}$ für $0 ≤ t < T$, außerhalb $0$.

4

Wie lautet die Basisfunktion $\varphi_1(t)$, die formgleich $s_1(t)$ ist?

	$\varphi_1(t) = s_1(t)$,
	$\varphi_1(t) = (1/T)^{\rm 0.5} \cdot \cos {2\pi t/T}$ für $0 ≤ t < T$, außerhalb $0$.
	$\varphi_1(t) = (2/T)^{\rm 0.5} \cdot \cos {2\pi t/T}$ für $0 ≤ t < T$, außerhalb $0$.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.