Exercise 4.06Z: Signal Space Constellations

• Return to book

Drei Signalraumkonstellationen

Die (mittlere) Fehlerwahrscheinlichkeit eines optimalen Binärsystems lautet:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$

Hierzu ist anzumerken:

• ${\rm Q}(x)$ bezeichnet die komplementäre Gaußsche Fehlerfunktion (Definition und Approximation):

$${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \approx \\ \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

• $d$ gibt den Abstand der beiden Sendesignalpunkte $s_0$ und $s_1$ im vorgegebenen Vektorraum an:

$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$

• $\sigma_n^2$ ist die Varianz des AWGN–Rauschens nach dem Detektor, der zum Beispiel als Matched–Filter realisiert sein kann. Es gelte $\sigma_n^2 = N_0/2$.

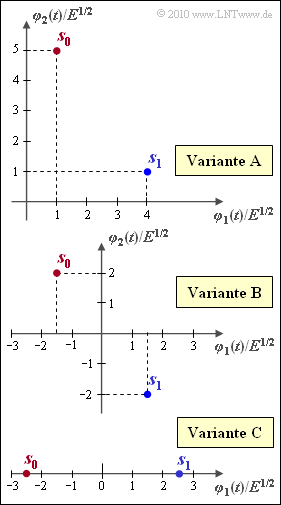
Durch die Grafik sind drei unterschiedliche Signalraumkonstellationen gegeben, nämlich

• Variante A: $s_0 = (+1, \ \, +5), \hspace{0.4cm} s_1 = (+4, \ \, +1)$,
• Variante B: $s_0 = (–1.5, \ \, +2), \, \ s_1 = (+1.5, \ \, –2)$,
• Variante C: $s_0 = (–2.5, \ \, 0), \hspace{0.5cm} s_1 = (+2.5, \ \, 0)$.

Die jeweils mittlere Energie pro Symbol ($E_{\rm S}$) kann nach folgender Gleichung berechnet werden:

$$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Kapitel Approximation der Fehlerwahrscheinlichkeit.
• Wenn bei einer Teilaufgabe keine anderslautende Angabe gemacht ist, so kann von gleichwahrscheinlichen Symbolen ausgegangen werden:

$${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$

1. Die Normierungsenergie $E$ ist hier stillschweigend zu $1$ gesetzt.

Fragebogen

1

Multiple-Choice

	correct
	false

2

Input-Box Frage

$xyz$ = $ab$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)