Exercise 1.09: BPSK and 4-QAM

Phasendiagramme von BPSK und 4–QAM

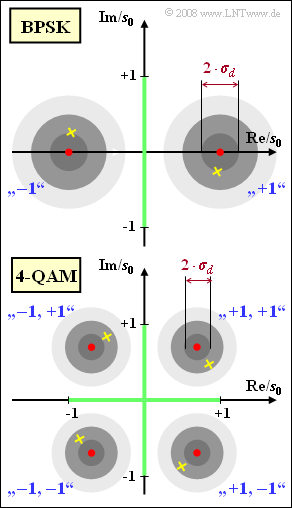
Die Grafik zeigt schematisch die Phasendiagramme der binären Phasenmodulation (abgekürzt BPSK) und der Quadraturamplitudenmodulation (4–QAM genannt). Die letztere lässt sich durch zwei BPSK–Systeme mit Cosinus– und Minus–Sinus–Träger beschreiben, wobei bei jedem der Teilkomponenten die Sendeamplitude gegenüber der BPSK um den Faktor „Wurzel aus 2” reduziert ist. Die Hüllkurve des Gesamtsignals $s(t)$ ist somit ebenfalls konstant gleich $s_{0}$. Die Fehlerwahrscheinlichkeit abhängig vom Quotienten $E_{\rm B}/N_{0}$ lautet bei BPSK und 4–QAM gleichermaßen:

$$p_{\rm B} = \ {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{E_{\rm B}/{ N_0 }} \right ).$$

Die Fehlerwahrscheinlichkeit des BPSK–Systems kann aber auch in der Form

$$p_{\rm B,\hspace{0.04cm}BPSK} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{T_{\rm B}}}$$

dargestellt werden. Entsprechend gilt für das 4–QAM–System:

$$p_{\rm B,\hspace{0.04cm}QAM} = {\rm Q}\left ( \frac{s_0/\sqrt{2}}{\sigma_d } \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$

Beide Gleichungen gelten allerdings nur unter der Voraussetzung einer exakten Phasensynchronisation. Bei einem Phasenversatz $\Delta\phi_{\rm T}$ zwischen sender– und empfangsseitigem Trägersignal erhöht sich die Fehlerwahrscheinlichkeit signifikant, wobei BPSK– und QAM–System unterschiedlich degradiert werden. Im Phasendiagramm macht sich der Phasenversatz durch eine Rotation der Punktwolken bemerkbar. In der Grafik sind die Mittelpunkte der Punktwolken für $\Delta\phi_{\rm T} = 15°$ durch gelbe Kreuze markiert, während die roten Kreise die Mittelpunkte für $\Delta\phi_{\rm T} = 0$ angeben. Es gilt stets $E_{\rm B}/N_{0} = 8$, so dass sich die Fehlerwahrscheinlichkeiten von BPSK und QAM im günstigsten Fall (ohne Phasenversatz) jeweils wie folgt ergeben $\Rightarrow$ Aufgabe Z1.8:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$

Bezeichnet man den Abstand der BPSK–Nutzabtastwerte von der (vertikalen) Entscheiderschwelle mit $s_{0}$, so ergibt sich für den Rauscheffektivwert $\sigma_{d} = s_{0}/4$. Die helleren Kreise in der Grafik markieren die Höhenlinien mit dem Radius $2\sigma_{d}$ bzw. $3\sigma_{d}$ der Gaußschen 2D–WDF.

Bei der 4–QAM sind gegenüber der BPSK die Abstände der rot eingezeichneten Nutzabtastwerte von den nun zwei Entscheiderschwellen jeweils um den Faktor „Wurzel aus 2” geringer, aber es ergibt sich auch ein um den gleichen Faktor kleinerer Rauscheffektivwert $\sigma_{d}$.

Hinweis:

Die Aufgabe bezieht sich auf die Seite Phasenversatz zwischen Sender und Empfänger im Lineare digitale Modulation – Kohärente Demodulation.
Die Werte der Q–Funktion können Sie mit folgenden Interaktionsmodul ermitteln: Komplementäre Gaußsche Fehlerfunktionen

Fragebogen

Musterlösung

Solution

(1) Durch die Rotation des Phasendiagramms um $\Delta\phi_{\rm T} = 15°$ wird der Abstand der Nutzabtastwerte von der Schwelle um cos$(15°) \approx 0.966$ geringer. Daraus folgt:

$$p_{\rm B} = {\rm Q}(0.966 \cdot 4) \approx {\rm Q}(3.86)\hspace{0.1cm}\underline {= 0.57 \cdot 10^{-4}}.$$

(2) Analog zu Teilaufgabe (1) erhält man mit cos$(45°) \approx 0.707$:

$$p_{\rm B} = {\rm Q}(0.707 \cdot 4) \approx {\rm Q}(2.83)\hspace{0.1cm}\underline {= 0.233 \cdot 10^{-2}}.$$

(3) Bei 4–QAM wird durch die Rotation um $\Delta\phi_{\rm T}$ im Uhrzeigersinn der Abstand

von der horizontalen Schwelle (Entscheidung des ersten Bits) gleich $s_{0} \cdot \cos(45° + \Delta\phi_{\rm T})$, also kleiner als ohne Phasenversatz,
von der vertikalen Schwelle (Entscheidung des zweiten Bits) gleich $s_{0} \cdot \cos(45° + \Delta\phi_{\rm T})$, also größer als ohne Phasenversatz.

Damit erhält man für die mittlere Fehlerwahrscheinlichkeit:

$$p_{\rm B} = \frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ+{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}} \right ) + \frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ-{\rm \Delta} \phi_{\rm T}) \cdot s_0}{0.25 \cdot s_0 / \sqrt{2}}\right ).$$

Hierbei ist der kleinere Rauscheffektivwert der 4–QAM bereits berücksichtigt. Zur Kontrolle berechnen wir die Fehlerwahrscheinlichkeit für $\Delta\phi_{\rm T} = 0$:

$$p_{\rm B} = \frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +\frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(45^\circ) \cdot 4}{1 / \sqrt{2}} \right )= {\rm Q}(4) = 0.317 \cdot 10^{-4}.$$

Dagegen erhält man mit $\Delta\phi_{\rm T} = 15°$:

$$p_{\rm B} = \ \frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(60^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +\frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(30^\circ) \cdot 4}{1 / \sqrt{2}} \right )=\\ = \ \frac{1}{2} \cdot \left [{\rm Q}(2.83)+ {\rm Q}(4.90)\right] \approx \frac{1}{2} \cdot \left [0.233 \cdot 10^{-2}+ 0.479 \cdot 10^{-6}\right] \hspace{0.1cm}\underline {= 0.117 \cdot 10^{-2}}.$$

(4) Bei einem Phasenversatz von $45°$ erhält man aus der oben allgemein hergeleiteten Gleichung:

$$p_{\rm B} = \ \frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(90^\circ) \cdot 4}{1 / \sqrt{2}} \right ) +\frac{1}{2} \cdot {\rm Q}\left ( \frac{\cos(0^\circ) \cdot 4}{1 / \sqrt{2}} \right )=\\ = \ \frac{1}{2} \cdot \left [{\rm Q}(0)+ {\rm Q}(5.66)\right] \hspace{0.1cm}\underline {\approx 0.25}.$$

Das heißt: Die Fehlentscheidung für das erste Bit ist $50\%$. Dagegen wird das zweite Bit nahezu fehlerfrei $(\approx 10^{–8})$ entschieden. Insgesamt ergibt sich so eine mittlere Fehlerwahrscheinlichkeit von ca. $25\%$.