Exercise 4.09: Decision Regions at Laplace

Drei verschiedene Entscheidungsregionen für Laplace

Wir betrachten ein Übertragungssystem, basierend auf den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$. Die zwei gleichwahrscheinlichen Sendesignale sind durch die Signalpunkte

$$\boldsymbol{ s }_0 = (-\sqrt{E}, \hspace{0.1cm}-\sqrt{E})\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (+\sqrt{E}, \hspace{0.1cm}+\sqrt{E})\hspace{0.05cm}$$

gegeben. Im Folgenden normieren wir zur Vereinfachung den Energieparameter zu $E = 1$ und erhalten somit

$$\boldsymbol{ s }_0 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (-1, \hspace{0.1cm}-1) \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_0\hspace{0.05cm}, $$

$$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (+1, \hspace{0.1cm}+1)\hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_1\hspace{0.05cm}.$$

Die Nachrichten $m_0$ und $m_1$ sind den so festgelegten Signalen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ eindeutig zugeordnet.

Die zwei Rauschkomponenten $n_1(t)$ und $n_2(t)$ seien unabhängig voneinander und jeweils laplace–verteilt mit Parameter $a = 1$:

$$p_{n_1} (\eta_1) = {1}/{2} \cdot {\rm e}^{- | \eta_1|} \hspace{0.05cm}, \hspace{0.2cm} p_{n_2} (\eta_2) = {1}/{2} \cdot {\rm e}^{- | \eta_2|} \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} \boldsymbol{ p }_{\boldsymbol{ n }} (\eta_1, \eta_2) = {1}/{4} \cdot {\rm e}^{- | \eta_1|- | \eta_2|} \hspace{0.05cm}. $$

Die Eigenschaften eines solchen Laplace–Rauschens werden in der Aufgabe Z4.9 noch eingehend behandelt.

Das Empfangssignal $\boldsymbol{r}$ setzt sich additiv aus dem Sendesignal $\boldsymbol{s}$ und dem Rauschsignal $\boldsymbol{n}$ zusammen:

$$\boldsymbol{ r } \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \boldsymbol{ s } + \boldsymbol{ n } \hspace{0.05cm}, \hspace{0.45cm}\boldsymbol{ r } = ( r_1, r_2) \hspace{0.05cm},$$

$$ \boldsymbol{ s } \hspace{-0.1cm} \ = \ \hspace{-0.1cm} ( s_1, s_2) \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol{ n } = ( n_1, n_2) \hspace{0.05cm}. $$

Die entsprechenden Realisierungen sind wie folgt bezeichnet:

$$\boldsymbol{ s }\hspace{-0.1cm} \ : \ \hspace{-0.1cm} \hspace{0.1cm} (s_{01},s_{02}){\hspace{0.15cm}\rm bzw. \hspace{0.15cm}} (s_{11},s_{12}) \hspace{0.05cm},$$

$$ \boldsymbol{ r } \hspace{-0.1cm} \ : \ \hspace{-0.1cm} \hspace{0.1cm} (\rho_{1},\rho_{2}) \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol{ n }: \hspace{0.1cm} (\eta_{1},\eta_{2}) \hspace{0.05cm}.$$

Die Entscheidungsregel des MAP– und des ML–Empfängers (beide sind aufgrund der gleichen Symbolwahrscheinlichkeiten identisch) lauten:

Entscheide für das Symbol $m_0$, falls

$$p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } ( \rho_{1},\rho_{2} |m_0 ) > p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\rho_{1},\rho_{2} |m_1 ) \hspace{0.05cm}.$$

Mit den weiteren Voraussetzungen kann hierfür (Entscheidung für $m_0$) auch geschrieben werden:

$${1}/{4} \cdot {\rm exp}\left [- | \rho_1 +1|- | \rho_2 +1| \hspace{0.1cm} \right ] > {1}/{4} \cdot {\rm exp}\left [- | \rho_1 -1|- | \rho_2 -1| \hspace{0.1cm} \right ] $$

$$\Rightarrow \hspace{0.3cm} | \rho_1 +1|+ | \rho_2 +1| < | \rho_1 -1|+ | \rho_2 -1|$$

$$\Rightarrow \hspace{0.3cm} L (\rho_1, \rho_2) = | \rho_1 +1|+ | \rho_2 +1| - | \rho_1 -1|- | \rho_2 -1| < 0 \hspace{0.05cm}.$$

Auf diese Funktion $L(\rho_1, \rho_2)$ wird in den nachfolgenden Aufgaben häufig Bezug genommen.

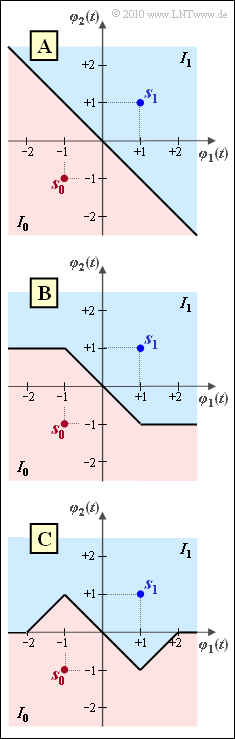
Die Grafik zeigt drei verschiedene Entscheidungsregionen ($I_0, I_1$). Bei AWGN–Rauschen wäre nur die obere Variante A optimal. Auch beim hier betrachteten Laplace–Rauschen führt die Variante A zur kleinstmöglichen Fehlerwahrscheinlichkeit, siehe Aufgabe Z4.9:

$$p_{\rm min} = {\rm Pr}({\cal{E}} \hspace{0.05cm}|\hspace{0.05cm} {\rm optimaler\hspace{0.15cm} Empf\ddot{a}nger}) = {\rm e}^{-2} \approx 13.5\,\%\hspace{0.05cm}.$$

Zu untersuchen ist, ob die Variante B bzw. die Variante C ebenfalls optimal ist, das heißt, ob auch deren Fehlerwahrscheinlichkeiten kleinstmöglich gleich $\rho_{\rm min}$ sind.

Hinweis:

Die Aufgabe bezieht sich auf die letzten Theorieseiten des Kapitels Approximation der Fehlerwahrscheinlichkeit.

Fragebogen

Musterlösung

Solution

(1) Die Verbundwahrscheinlichkeitsdichten unter den Bedingungen $m_0$ bzw. $m_1$ lauten:

$$p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } ( \rho_{1},\rho_{2} |m_0 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{4} \cdot {\rm exp}\left [- | \rho_1 +1|- | \rho_2 +1| \hspace{0.05cm} \right ]\hspace{0.05cm},$$

$$p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } ( \rho_{1},\rho_{2} |m_1 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{4} \cdot {\rm exp}\left [- | \rho_1 -1|- | \rho_2 -1| \hspace{0.05cm} \right ]\hspace{0.05cm}.$$

Bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$ lautet die MAP–Entscheidungsregel: Entscheide für das Symbol $m_0$ ⇔ Signal $s_0$, falls

$$p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } ( \rho_{1},\rho_{2} |m_0 ) > p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\rho_{1},\rho_{2} |m_1 ) \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} {1}/{4} \cdot {\rm exp}\left [- | \rho_1 +1|- | \rho_2 +1| \hspace{0.05cm} \right ] > {1}/{4} \cdot {\rm exp}\left [- | \rho_1 -1|- | \rho_2 -1|\hspace{0.05cm} \right ] $$

$$\Rightarrow \hspace{0.3cm} | \rho_1 +1|+ | \rho_2 +1| < | \rho_1 -1|+ | \rho_2 -1|$$

$$\Rightarrow \hspace{0.3cm} L (\rho_1, \rho_2) = | \rho_1 +1|- | \rho_1 -1|+ | \rho_2 +1| - | \rho_2 -1| < 0 \hspace{0.05cm}.$$

Richtig sind demnach die Lösungsvorschläge 1 und 2.

(2) Alle Aussagen treffen zu: Für $x ≥ 1$ ist

$$| x +1|- | x -1| = x +1 -x +1 =2 \hspace{0.05cm}.$$

Ebenso gilt für $x ≤ \, –1$, zum Beispiel $x = \, –3$:

$$| x +1|- | x -1| = | -3 +1|- | -3 -1| = 2-4 = -2 \hspace{0.05cm}.$$

Dagegen gilt im mittleren Bereich $–1 ≤ x – +1$:

$$| x+1|- | x -1| = x +1 -1 +x =2x \hspace{0.05cm}.$$

(3) Das Ergebnis von Teilaufgabe (1) lautete: Entscheide für das Symbol $m_0$, falls

$$L (\rho_1, \rho_2) = | \rho_1 +1| - | \rho_1 -1|+ | \rho_2 +1| - | \rho_2 -1| < 0 \hspace{0.05cm}.$$

Im betrachteten (inneren) Bereich $–1 ≤ \rho_1 ≤ +1$, $–1 ≤ \rho_2 ≤ +1$ gilt mit dem Ergebnis der Teilaufgabe (2):

$$| \rho_1+1| - | \rho_1 -1| = 2\rho_1 \hspace{0.05cm}, \hspace{0.2cm} | \rho_2+1| - | \rho_2 -1| = 2\rho_2 \hspace{0.05cm}.$$

Setzt man dieses Ergebnis oben ein, so ist genau dann für $m_0$ zu entscheiden, falls

$$L (\rho_1, \rho_2) = 2 \cdot ( \rho_1+\rho_2) < 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \rho_1+\rho_2 < 0\hspace{0.05cm}.$$

Richtig ist also der Lösungsvorschlag 1.

(4) Für $\rho_1 > 1$ ist $|\rho_1+1| \, –|\rho_1 \, –1| = 2$, während für $D_2 = |\rho_2+1| \, –|\rho_2 \, –1|$ alle Werte zwischen $–2$ und $+2$ möglich sind. Die Entscheidungsgröße ist somit $L(\rho_1, \rho_2) = 2 + D_2 ≥ 0$. In diesem Fall führt die Regel zu einer $m_1$–Entscheidung. Richtig ist demnach hier der Lösungsvorschlag 2.

(5) Nach ähnlicher Rechnung wie in der Teilaufgabe (3) kommt man zum Ergebnis:

$$L (\rho_1, \rho_2) = -2 + D_2 \le 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Entscheidung\hspace{0.15cm} auf\hspace{0.15cm}} m_0\hspace{0.05cm},$$

was dem Lösungsvorschlag 1 entspricht.

(6) Ähnlich der Teilaufgabe (4) gilt hier:

$$D_1 = | \rho_1 +1| - | \rho_1 -1| \in \{-2, ... \hspace{0.05cm} , +2 \} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}L (\rho_1, \rho_2) = 2 + D_1 \ge 0 \hspace{0.05cm}.$$

Richtig ist also hier der Lösungsvorschlag 2: Entscheidung auf $m_1$.

(7) Nach ähnlicher Überlegung wie in der letzten Teilaufgabe kommt man zum Ergebnis:

$$L (\rho_1, \rho_2) = -2 + D_1 \le 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Entscheidung\hspace{0.15cm} auf\hspace{0.15cm}} m_0\hspace{0.05cm}.$$

Dies entspricht dem Lösungsvorschlag 1.

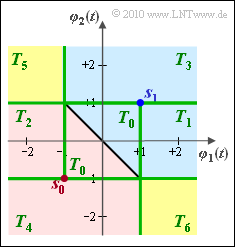
(8) Die Ergebnisse der Teilaufgaben (3) bis (7) sind in der folgenden Grafik zusammengefasst:

Teilgebiet T_0: Entscheidung auf $m_0$ bzw. $m_1$ gemäß Aufgabe (3).

Zusammenfassung der Ergebnisse

Teilgebiet T_1: Entscheidung auf $m_1$ gemäß Aufgabe (4).
Teilgebiet T_2: Entscheidung auf $m_0$ gemäß Aufgabe (5).
Teilgebiet T_3: Entscheidung auf $m_1$ gemäß Aufgabe (6).
Teilgebiet T_4: Entscheidung auf $m_0$ gemäß Aufgabe (7).
Teilgebiet T_5: Nach dem Ergebnis von Aufgabe (5) sollte man auf $m_0$ entscheiden, nach Aufgabe (6) auf $m_1$. Das bedeutet: Bei Laplace–Rauschen ist es egal, ob man $T_5$ der Region $I_0$ oder $I_1$ zuordnet.
Teilgebiet T_6: Auch dieses Gebiet kann man aufgrund der Ergebnisse von Aufgabe (4) und (7) sowohl der Region $I_0$ als uach der Region $I_1$ zuordnen.

Für die Teilaufgabe $T_0, \ ... \ , T_4$ gibt es eine feste Zuordnung zu den Entscheidungsregionen $I_0$ (rot) bzw. $I_1$ (blau). Dagegen können die beiden gelb markierten Bereiche $T_5$ und $T_6$ ohne Verlust an Optimalität sowohl $I_0$ als auch $I_1$ zugeordnet werden. Vergleicht man diese Grafik mit den Varianten $A, B und C auf der Angabenseite, so erhält man das Ergebnis: * Die Varianten A und B sind gleich gut und beide sind optimal. Die Fehlerwahrscheinlichkeit ergibt sich in beiden Fällen zu $p_{\rm min} = {\rm e}^{\rm –2}$. * Die Variante C ist nicht optimal; bezüglich der Teilaufgabe $T_1$ und $T_2$ gibt es Fehlzuordnungen. Die Fehlerwahrscheinlichkeit ist demzufolge größer als $p_{\rm min}$. Richtig sind also die Vorschläge 1 und 2.

	$\rho_{\it r\|m}(\rho_1, \ \rho_2\|m_0) > p_{\it r\|m}(\rho_1, \ \rho_2\|m_1)$,
	$L(\rho_1, \ \rho_2) = \|\rho_1+1\| \, –\|\rho_1 \, –1\| + \|\rho_2+1\| \, –\|\rho_2 \, –1\| < 0$,
	$L(\rho_1, \ \rho_2) = \rho_1 + \rho_2 ≥ 0$.

	Für $x ≥ 1$ ist $\|x + 1\| \, –\|x \, –1\| = 2$.
	Für $x ≤ \, –1$ ist $\|x+1\| \, –\|x \, –1\| = \, –2$.
	Für $–1 ≤ x ≤ 1$ ist $\|x+1\| \, –\|x \, –1\| = 2x$.

	Entscheidung für $m_0$, falls $\rho_1 + \rho_2 < 0$.
	Entscheidung für $m_1$, falls $\rho_1 + \rho_2 < 0$.

	Entscheidung für $m_0$ im gesamten Bereich.
	Entscheidung für $m_1$ im gesamten Bereich.
	Entscheidung für $m_0$ nur, falls $\rho_1 + \rho_2 < 0$.

	Die Variante A führt zur minimalen Fehlerwahrscheinlichkeit.
	Die Variante B führt zur minimalen Fehlerwahrscheinlichkeit.
	Die Variante C führt zur minimalen Fehlerwahrscheinlichkeit.