Exercise 5.3: AWGN and BSC Model
From LNTwww
AWGN–Kanal und BSC–Modell
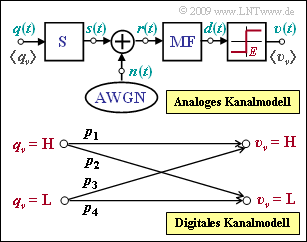
Die Grafik zeigt oben das analoge Kanalmodell eines digitalen Übertragungssystems, wobei das additive Rauschsignal $n(t)$ mit der Rauschleistungsdichte $N_0/2$ wirksam ist. Es handelt sich um AWGN–Rauschen. Die Varianz des Rauschanteils vor dem Entscheider (nach dem Matched–Filter) ist dann
- $$\sigma^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$
Weiter soll gelten:
- Es treten keine Impulsinterferenzen auf. Wurde das Symbol $q_{\nu} = \boldsymbol{\rm H} \mathbf{H}$ gesendet, so ist der Nutzanteil des Detektionssignal gleich $+s_0$, bei $q_{\nu} = \boldsymbol{L}$ dagegen $–s_0$.
- Der Schwellenwertentscheider berücksichtigt eine Schwellendrift, das heißt, die Schwelle E kann durchaus vom Optimalwert $E = 0$ abweichen. Die Entscheidungsregel lautet:
- $$\upsilon_\nu = \left\{ \begin{array}{c} \mathbf{H} \\ \mathbf{L} \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}d (\nu \cdot T) > E \hspace{0.05cm}, \\ {\rm falls} \hspace{0.15cm} d (\nu \cdot T) \le E\hspace{0.05cm}.\\ \end{array}$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
