Exercise 1.7: Coding for Broadband ISDN
Beim herkömmlichen ISDN über Kupferleitungen wird der HDB3–Code verwendet (siehe Aufgabe A1.5). Dieser wurde vom sog. AMI–Code abgeleitet, ist wie dieser ein Pseudoternärcode, vermeidet aber mehr als drei aufeinander folgende „$0$”–Symbole, indem die strenge AMI–Codierregel bei längeren Nullfolgen bewusst verletzt wird.
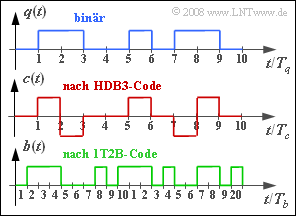
Die Grafik zeigt das HDB3–codierte Signal $c(t)$, das sich aus dem binären redundanzfreien Quellensignal $q(t)$ ergibt. Da im Quellensignal nicht mehr als drei aufeinanderfolgende Nullen auftreten, ist $c(t)$ identisch mit dem AMI–codierten Signal.
Das Ende der 1990–Jahre geplante Breitband–ISDN sollte Datenraten bis $155 \ \rm Mbit/s$ bereitstellen im Vergleich zu $144 \ \rm kbit/s$ des herkömmlichen ISDN mit zwei B–Kanälen und einem D–Kanal). Um diese hohe Datenrate zu erreichen, musste zum einen eine neuere Technik (ATM) verwendet werden, zum zweiten aber auch das Übertragungsmedium gewechselt werden, von der Kupferleitung zur Glasfaser.
Da das HDB3–codierte Signal $c(t) ∈ \{–1, 0, +1\}$ aber mittels Licht nicht übertragen werden kann, war eine zweite Codierung erforderlich. Der hierfür vorgesehene 1T2B–Code ersetzt jedes Ternärsymbol durch zwei Binärsymbole. Das untere Diagramm zeigt beispielhaft das Binärsignal $b(t) ∈ \{0, 1\}$, das sich nach dieser 1T2B–Codierung aus dem Signal $c(t)$ ergibt.
Gehen Sie bei dieser Aufgabe davon aus, dass die Bitrate des redundanzfreien Quellensignals $q(t)$ gleich $R_{q} = 2.048 \ \rm Mbit/s$ beträgt. Die jeweiligen Symboldauern der Signale $q(t), c(t)$ und $b(t)$ werden mit $T_{q}, T_{c}$ und $T_{b}$ bezeichnet.
Die äquivalente Bitrate des pseudoternären Signals $c(t)$ ist $R_{c} = {\rm ld}(3)/T_{c}$, woraus mit der (echten) Bitrate $R_{q} = 1/T_{q}$ des Quellensignals die relative Redundanz des AMI– bzw. HDB3–Codes berechnet werden kann:
- $$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm ld}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm ld}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$
Für den 1T2B–Code kann eine ähnliche Gleichung aufgestellt werden, ebenso wie für die beiden Codes in Kombination.
Hinweis:
Die Aufgabe gehört zum Weiterentwicklungen von ISDN des vorliegenden Buches. Die Redundanz wird im Grundlagen der codierten Übertragung des Buches „Digitalsignalübertragung” definiert und an Beispielen verdeutlicht.
Fragebogen
Musterlösung
(1) (2) (3) (4) (5) (6) (7)