Exercise 3.14: Error Probability Bounds
From LNTwww
Für den häufig verwendeten Faltungscode mit
- der Coderate $R = 1/2$,
- dem Gedächtnis $m = 2$,
- der Übertragungsfunktionsmatrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big ) $$
lautet die Erweiterte Pfadgewichtsfunktion:
- $$T_{\rm enh}(X, U) = \frac{UX^5}{1- 2 \hspace{0.05cm}U \hspace{-0.05cm}X} \hspace{0.05cm}.$$
Mit der schon häufiger benutzten Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + \ ... $ kann hierfür auch geschrieben werden:
- $$T_{\rm enh}(X, U) = U X^5 \cdot \left [ 1 + (2 \hspace{0.05cm}U \hspace{-0.05cm}X) + (2 \hspace{0.05cm}U\hspace{-0.05cm}X)^2 + (2 \hspace{0.05cm}U\hspace{-0.05cm}X)^3 + ... \hspace{0.10cm} \right ] \hspace{0.05cm}.$$
Die „einfache” Pfadgewichtsfunktion $T(X)$ ergibt sich daraus, wenn man die zweite Variable $U = 1$ setzt.
Anhand dieser Funktionen können Fehlerwahrscheinlichkeitsschranken angegeben werden:
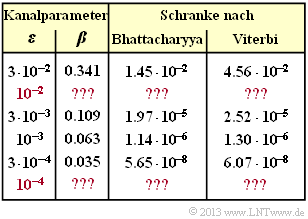
- Die Burstfehlerwahrscheinlichkeit wird durch die Bhattacharyya–Schranke begrenzt:
- $${\rm Pr(Burstfehler)} \le {\rm Pr(Bhattacharyya)} = T(X = \beta) \hspace{0.05cm}.$$
- Dagegen ist die Bitfehlerwahrscheinlichkeit stets kleiner (oder gleich) der Viterbi–Schranke:
- $${\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac [[:Template:\rm d]]{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1}} \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Kapitel ....
- Der Bhattacharyya–Parameter für BSC lautet:
- $$\beta = 2 \cdot \sqrt{\varepsilon \cdot (1- \varepsilon)} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)