Exercise 4.1: Log Likelihood Ratio

Betrachtete Kanalmodelle

Zur Interpretation von Log–Likelihood–Verhältnissen (kurz $L$–Werten) gehen wir wie im Theorieteil vom Binary Symmetric Channel (BSC) aus. Die englische Bezeichung ist Log Likelihood Ratio (LLR).

Für die binären Zufallsgrößen am Eingang und Ausgang gelte

$$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$

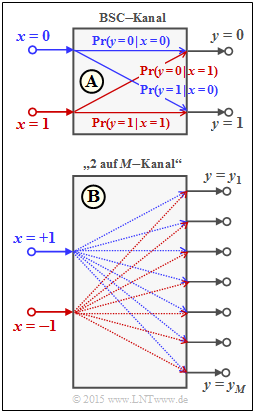
Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als Modell A bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:

$${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$

$${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$

Die Verfälschungswahrscheinlichkeit $\epsilon$ ist der entscheidende Parameter des BSC–Modells.

Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ das Log Likelihood Ratio (LLR) zu betrachten.

Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition:

$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$

wobei der Index „A” auf die Apriori–Wahrscheinlichkeit hinweist.

Beispielsweise ergibt sich für ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ das Apriori–LLR $L_{\rm A}(x) = \, –1.382$.

Aus dem BSC–Modell lässt sich zudem der $L$–Wert der bedingten Wahrscheinlichkeiten ${\rm Pr}(y|x)$ in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit $L_{\rm V}(y)$ bezeichnet wird:

$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.05cm} y = 0, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$

Beispielsweise ergibt sich für $\epsilon = 0.1$:

$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$

Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten ${\rm Pr}(x|y)$, die mit den Vorwärtswahrscheinlichkeiten ${\rm Pr}(y|x)$ sowie den Eingangswahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ über den Satz von Bayes in Zusammenhang stehen. Der entsprechende $L$–Wert wird in dieser Aufgabe mit $L_{\rm R}(y)$ bezeichnet:

$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$

Hinweise:

Die Aufgabe bezieht sich auf die ersten Seiten des Kapitels Soft–in Soft–out Decoder.
In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen $L_{\rm A}, \ L_{\rm V}$ und $L_{\rm R}$ auch auf den unten skizzierten „2–auf–$M$–Kanal” übertragen werden können. Hierzu wählen wir für die Eingangssymbole eine bipolare Betrachtungsweise: „$0$” → „$+1$” sowie „$1$” → „$–1$”.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

Musterlösung

Solution

(1) Für die bedingten Wahrscheinlichkeiten gilt nach dem Satz von Bayes mit der Schnittmenge $A ∩ B$:

$$\rm Pr(\it B \hspace{0.05cm}|\hspace{0.05cm} \it A) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it A)}\hspace{0.05cm}, \hspace{0.3cm} \rm Pr(\it A \hspace{0.05cm}|\hspace{0.05cm} \it B) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it B)}$$

$$\Rightarrow \hspace{0.3cm} \rm Pr(\it A \hspace{0.05cm}|\hspace{0.05cm} \it B) = \rm Pr(\it B \hspace{0.05cm}|\hspace{0.05cm} \it A) \cdot \frac{\rm Pr(\it A)}{\rm Pr(\it B)}\hspace{0.05cm}.$$

Richtig ist der Lösungsvorschlag 3. Im Sonderfall ${\rm Pr}(B) = {\rm Pr}(A)$ wäre auch der Vorschlag 1 richtig.

(2) Mit $A$ ⇒ „$x = 0$” und $B$ ⇒ „$y = 0$” ergibt sich sofort die Gleichung gemäß Lösungsvorschlag 1:

$${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$

(3) Wir berechnen den $L$–Wert der Rückschlusswahrscheinlichkeiten. Unter der Annahme $y = 0$ gilt:

$$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = $$

$$\ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} = $$

$$\ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)} + {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}$$

$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$

In gleicher Weise ergibt sich unter er Annahme $y = 1$:

$$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$

Die beiden Ergebnisse lassen sich mit $y ∈ \{0, \, 1\}$ und

dem Eingangs–LLR,

$$L_{\rm A}(x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}\hspace{0.05cm},$$

sowie dem Vorwärts–LLR,

$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} \hspace{0.05cm},$$

wie folgt zusammenfassen:

$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$

Die Identität $L_{\rm R} &equal; L_{\rm V}(y)$ erfordert $L_{\rm A}(x) = 0$ ⇒ gleichwahrscheinliche Symbole ⇒ Vorschlag 2.

(4) Der Aufgabenbeschreibung können Sie entnehmen, dass mit der Verfälschungswahrscheinlichkeit $\epsilon = 0.1$ der Ausgangswert $y = 1$ zum Vorwärts–LLR $L_{\rm V}(y = 1) = \, –2.197$ führt. Wegen ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$ gilt somit auch:

$$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{-2.197}\hspace{0.05cm}.$$

(5) Bei gleicher Verfälschungswahrscheinlichkeit $\epsilon = 0.1$ unterscheidet sich $L_{\rm V}(y = 0)$ von $L_{\rm V}(y = 1)$ nur durch das Vorzeichen. Mit ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, –1.382$ erhält man somit:

$$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$

(6) Wie Sie sicher gerne nachprüfen werden, gilt der Zusammenhang „$L_{\rm R} = L_{\rm V} + L_{\rm A}$” auch für den „2–auf–$M$–Kanal”, unabhängig vom Umfang $M$ des Ausgangsalphabets ⇒ Antwort Ja.

(7) Der AWGN–Kanal wird durch den skizzierten „2–auf–$M$–Kanal” mit $M &8594; ∞$ ebenfalls beschrieben ⇒ Antwort Ja.

	${\rm Pr}(A \| B) = {\rm Pr}(B \| A)$,
	${\rm Pr}(A \| B) = {\rm Pr}(B \| A) \cdot {\rm Pr}(B) / {\rm Pr}(A)$,
	${\rm Pr}(A \| B) = {\rm Pr}(B \| A) \cdot {\rm Pr}(A) / {\rm Pr}(B)$.

	${\rm Pr}(x = 0 \| y = 0) = {\rm Pr}(y = 0 \| x = 0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)$,
	${\rm Pr}(x = 0 \| y = 0) = {\rm Pr}(y = 0 \| x = 0) \cdot {\rm Pr}(y = 0) / {\rm Pr}(x = 0)$.

	Für jede beliebige Eingangsverteilung ${\rm Pr}(x = 0), \ {\rm Pr}(x = 1)$.
	Nur für die Gleichverteilung: $\hspace{0.2cm} {\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2$.

	Ja.
	Nein.

	Ja.
	Nein.