Exercise 1.12: Hard Decision vs. Soft Decision

• Return to book

Blockfehlerrate des (7, 4, 3)-Codes bei Hard Decision und Soft Decision

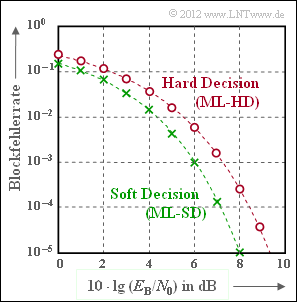
Die Abbildung zeigt die Blockfehlerwahrscheinlichkeit für den (7, 4, 3)–Hamming–Code, wobei für den Empfänger zwei Varianten berücksichtigt sind:

• Bei Maximum–Likelihood–Detektion mit harten Entscheidungen (Hard Decision, HD), die im vorliegenden Fall (perfekter Code) auch durch Syndromdecodierung realisiert werden kann, ergibt sich die rote Kurve (Kreismarkierung).

• Der Kanal kann bei Hard Decision vereinfacht durch das BSC–Modell ersetzt werden. Der Zusammenhang zwischen dem BSC–Parameter $\varepsilon$ und dem AWGN–Quotienten $E_{\rm B}/N_{0}$ (in der Grafik verwendet) ist wie folgt gegeben:

$$\varepsilon = {\rm Q}\left ( \sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \right ) \hspace{0.05cm}.$$

Hier bezeichnet Q(x) die komplementäre Gaußsche Fehlerfunktion und R die Coderate.

• Die grüne Kurve (Kreuze) zeigt die Blockfehlerwahrscheinlichkeit bei „weichen” Entscheidungen (Soft Decision, SD). Dieser Funktionsverlauf lässt sich nicht in geschlossen–mathematischer Form angeben. In der Grafik eingezeichnet ist eine in [Fri96] angegebene obere Schranke:

$${\rm Pr(Blockfehler)} \hspace{-0.15cm}\ \le \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{ 3 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right )+\\ \hspace{-0.15cm}\ + \ \hspace{-0.15cm}7 \cdot {\rm Q}\left ( \sqrt{ 4 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) + {\rm Q}\left ( \sqrt{ 7 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) \hspace{0.05cm}.$$

Der jeweils erste Faktor im Argument der Q–Funktion gibt die möglichen Hamming–Distanzen an: $i = 3, 4 {\rm und} 7$. Die Vorfaktoren berücksichtigen die Vielfachheiten $W_{3} = W_{4} = 7 {\rm und} W_{7} = 1$, und $R = 4/7$ beschreibt die Coderate. Für $10 · {\rm lg} \ E_{\rm B}/N_{0} > 8 \ {\rm dB}$ ist Pr(Blockfehler) kleiner als $10^{–5}$.

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel Decodierung linearer Blockcodes. Verwenden Sie für numerische Ergebnisse das folgende Berechnungsmodul:

Komplementäre Gaußsche Fehlerfunktion

Fragebogen

1

Wir betrachten bis einschließlich Teilaufgabe (4) stets Hard Decision. Welche Blockfehlerwahrscheinlichkeit besitzt der (7, 4, 3)–Hamming–Code?

$\varepsilon = 0.01: {\rm Pr(Blockfehler)}$ $\ \cdot 10^{-3}$

$\varepsilon = 0.001: {\rm Pr(Blockfehler)}$ $\ \cdot 10^{-5}$

2

Wie kann man die Fehlerwahrscheinlichkeit eines Hamming–Codes annähern?

	${\rm Pr(Blockfehler)} = n · (n–1)/2 · \varepsilon^2.$
	${\rm Pr(Blockfehler)} = n · \varepsilon^2.$
	${\rm Pr(Blockfehler)} = n · \varepsilon^n.$

3

Welcher Hamming–Code besitzt die kleinste Blockfehlerwahrscheinlichkeit bei konstantem BSC–Parameter $\varepsilon$?

	der Hamming–Code (3, 1, 3) ⇒ Repetition Code (3, 1, 3),
	der Hamming–Code (7, 4, 3),
	der Hamming–Code (15, 11, 3).

4

Welcher numerische Zusammenhang besteht zwischen dem BSC–Parameter $\varepsilon$ und dem AWGN–Quotienten $E_{\rm B}/N_{0}$?

$\varepsilon = 0.01: \ \ 10 · {\rm lg} \ E_{\rm B}/N_{0}$ $\ \rm dB$

$\varepsilon = 0.001: \ \ 10 · {\rm lg} \ E_{\rm B}/N_{0}$ $\ \rm dB$

5

Welcher Gewinn (in dB) ist durch Soft Decision (SD) zu erzielen, wenn die Blockfehlerwahrscheinlichkeit den Wert $10^{–5}$ nicht überschreiten soll?

$\ 10 · {\rm lg} G_{\rm SD}$ = $\ \rm dB$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.