Exercise 2.3Z: xDSL Frequency Band

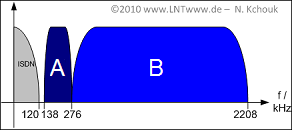
Vorgegebene xDSL-Frequenzbandbelegung

Die Abbildung zeigt die Frequenzbandbelegung eines gebräuchlichen xDSL–Systems. Im unteren Bereich befindet sich das ISDN–Band, danach folgen zwei Bänder $A$ und $B$, die für Downstream und Upstream stehen. Über die Reihenfolge der beiden Bänder wird nichts ausgesagt. Dies ist die Fragestellung zur Teilaufgabe 2).

Weiter ist bei xDSL/DMT standardisiert, dass

pro Sekunde $4000$ Rahmen übertragen werden,
nach $68$ Datenrahmen jeweils ein Synchronisationsrahmen eingefügt wird,
die Symboldauer wegen des zyklischen Präfix noch um den Faktor $16/17$ verkürzt werden muss,
jeder Datenrahmen zu einem DMT–Symbol codiert wird.

Damit ist auch die Integrationsdauer $T$ festgelegt, die beim Empfänger zur Detektion ausgewertet wird, und gleichzeitig auch die Grundfrequenz $f_{0} = 1/T$ des hier betrachteten DMT–Verfahrens (Discrete Multitone Transmission).

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel xDSL als Übertragungstechnik dieses Buches. Informationen zum zyklischen Präfix finden Sie im Kapitel Verfahren zur Senkung der Bitfehlerrate bei DSL.

Fragebogen

	ADSL,
	ADSL2+,
	VDSL.

	$A$ kennzeichnet den Upstream und $B$ den Downstream.
	$A$ kennzeichnet den Downstream und $B$ den Upstream.

$T \ = \ $

$\ \mu \rm s$

$ f_{0} \ = \ $

$\ \rm kHz$

$ K_{\rm max} \ = \ $

$K \ = \ $

$ b \ = \ $

$\ \rm bit$

Musterlösung

Solution

(1) Richtig ist der zweite Lösungsvorschlag. Bei ADSL endet das Frequenzband bei $1104 \ \rm kHz$. VDSL hat je nach Bandplan eine deutlich größere Bandbreite, wobei sich Upstream– und Downstream–Bänder jeweils abwechseln.

(2) Richtig ist der erste Lösungsvorschlag. Dem Upstream wurden die besseren (niedrigeren) Frequenzen zugewiesen, da sich ein Ausfall der wenigeren Upstream–Kanäle prozentual ungünstiger auswirkt als der Ausfall eines Downstream–Kanals.

(3) Ohne Berücksichtigung der Synchronisationsrahmen (nach jeweils $68$ nur mit Nutzdaten belegten Rahmen) und des Guard–Intervalls ergäbe sich für die Rahmendauer $T = 1/(4000/{\rm s}) = 250 \ \mu \rm s$. Mit Berücksichtigung dieses Overheads ist die Symboldauer um den Faktor $68/69 \cdot 16/17$ kürzer:

$$T = \frac{68}{69} \cdot \frac{16}{17} \cdot 250\, {\rm \mu s} \hspace{0.15cm}\underline{ \approx 232\, {\rm \mu s}} \hspace{0.05cm}.$$

(4) Die Subträger liegen bei DMT bei allen Vielfachen von $f_0$, wobei

$$f_0 = \frac{1}{T} \hspace{0.15cm}\underline{= 4.3125 \, {\rm kHz}}$$

gelten muss. Die Zeitfensterung entspricht nämlich der Multiplikation der cosinusförmigen Trägersignale mit einer Rechteckfunktion der Dauer $T$. Im Frequenzbereich ergibt sich damit die Faltung mit der si–Funktion. Würden die Systemgrößen $T$ und $f_0 = 1/T$ nicht aufeinander abgestimmt sein, so käme es zu einer De–Orthogonalisierung der einzelnen DMT–Kanäle und damit zu Intercarrier–Interferenzen.

(5) Ohne Berücksichtigung der ISDN/Upstream–Reservierung erhält man $K = 2208/4.3125 \underline{= 512}.$

(6) Die unteren $276/4.3125 = 64$ Kanäle sind beim hier betrachteten System ADSL2+ für ISDN und Upstream reserviert. Somit verbleiben $K = 512 – 64 \underline{= 448}$ nutzbare Kanäle.

(7) Für die Bitrate gilt

$$R_{\rm B} = 4000 \, \,\frac {\rm Rahmen}{\rm s} \cdot K \cdot b \hspace{0.05cm}.$$

Daraus ergibt sich für die (mittlere) Bitbelegung pro Subkanal (Bin):

$$b = \frac{R_{\rm B}}{ 4000 \, \, {\rm Rahmen}/{\rm s} \cdot K} = \frac{25 \cdot 10^6 \,\, {\rm bit/s}}{ 4000 \, \, {1}/{\rm s} \cdot 448} \hspace{0.15cm}\underline{= 13.95 \, \, {\rm bit}}\hspace{0.05cm}.$$