Exercise 1.2: ISDN and PCM
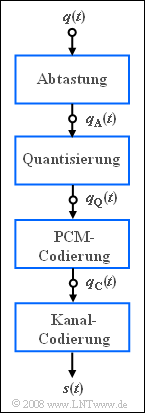
Die Umwandlung des analogen Sprachsignals $q(t)$ in das Binärsignal $q_{\rm C}(t)$ geschieht bei ISDN (Integrated Services Digital Network) entsprechend den Richtlinien der Pulscodemodulation (PCM) durch
- Abtastung im Abstand $T_{\rm A} = 1/f_{\rm A}$,
- Quantisierung auf $M = 256$ diskrete Werte,
- binäre PCM–Codierung mit $N$ Bit pro Quantisierungswert.
Die Netto–Datenrate eines so genannten $\rm B$–Kanals (Bearer Channel) ist $64 \ \rm kbit/s$ und entspricht der Bitrate des redundanzfreien Binärsignals $q_{\rm C}(t)$. Wegen der anschließenden redundanten Kanalcodierung und der eingefügten Signalisierungsbits ist allerdings die Brutto–Datenrate – also die Übertragungsrate des Sendesignals $s(t)$ – größer.
Ein Maß für die Qualität des gesamten (ISDN–)Übertragungssystems ist das Sinken–SNR
- $$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$
als das Verhältnis der Leistungen des auf den Bereich $300 \ {\rm Hz}\ \text{...}\ 3400 \ {\rm Hz}$ bandbegrenzten Analogsignals $q(t)$ und des Fehlersignals $\varepsilon (t) = v (t) - q(t)$. Für das Sinkensignal $\upsilon (t)$ wird hierbei eine ideale Signalrekonstruktion mit einem idealen rechteckförmigen Tiefpass vorausgesetzt.
Hinweis:
Die Aufgabe bezieht sich auf Allgemeine Beschreibung von ISDN dieses Buches sowie auf Pulscodemodulation des Buches „Modulationsverfahren”.
Fragebogen
Musterlösung
(1) Die Quantisierungsstufenzahl $M$ wird meist als Zweierpotenz gewählt und für die Bitanzahl $N = {\log_2}\hspace{0.05cm}(M)$.
Aus $M = 2^{8} = 256$ folgt $\underline{N = 8}$.
(2) Für die Bitrate gilt $R_{\rm B} = N \cdot f_{\rm A}$. Aus $R_{\rm B} = 64 \ \rm kbit/s$ und $N = 8$ erhält man somit $f_{\rm A} \hspace{0.15cm}\underline{= 8 \ \rm kHz}$.
(3) Durch die Bandbegrenzung ist die höchste im Signal $q(t)$ enthaltene Frequenz gleich $3.4 \ \rm kHz$. Nach dem Abtasttheorem müsste deshalb $f_{\rm A} ≥ 6.8 \ \rm kHz$ gelten. Mit $f_{\rm A} = 8 \ \rm kHz$ ist die Bedingung erfüllt ⇒ $\underline {\rm JA}$.
(4) Richtig sind die beiden letzten Aussagen:
- Auch wenn der Einfluss des AWGN–Rauschens gering ist (kleine Rauschleistungsdichte $N_{0}$), kann das Sinken–SNR $\rho_{v}$ einen durch das Quantisierungsrauschen gegebenen Grenzwert nicht unterschreiten:
- $$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$
- Bei größerer Rauschstörung wird $\rho_{v}$ durch die dann vorhandenen Übertragungsfehler weiter (signifikant) verringert.
- Dagegen führt die Abtastung zu keinem Qualitätsverlust, wenn das Abtasttheorem eingehalten wird.
- Die Abtastung kann dann vollständig rückgängig gemacht werden, wenn das Quellensignal $q(t)$ bandbegrenzt ist und die Signalrekonstruktion (ein idealer Tiefpass) richtig dimensioniert ist.