Exercise 4.3: Pointer Diagram Representation

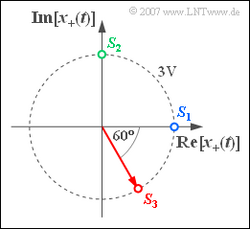
Wir betrachten ein analytisches Signal $x_+(t)$, welches durch das gezeichnete Diagramm in der komplexen Ebene festgelegt ist. Je nach Wahl der Signalparameter ergeben sich daraus drei physikalische BP–Signale $x_1(t)$, $x_2(t)$ und $x_3(t)$, die sich durch verschiedene Startpunkte $S_i = x_i(t = 0)$ unterscheiden (blauer, grüner und roter Punkt). Zudem seien auch die Winkelgeschwindigkeiten der drei Konstellationen unterschiedlich:

Das analytische Signal $x_{1+}(t)$ beginnt bei $S_1$ = 3 V. Die Winkelgeschwindigkeit ist $\omega_1 = \pi \cdot 10^{4} \ 1/\text{s}$.
Das Signal $x_{2+}(t)$ beginnt beim grünen Startpunkt $S_2 = {\rm j} \cdot 3 \ \text{V}$ und dreht gegenüber $x_{1+}(t)$ mit doppelter Winkelgeschwindigkeit ⇒ $\omega_2 = 2 \cdot \omega_1$.
Das Signal $x_{3+}(t)$ beginnt beim rot markierten Ausgangspunkt $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\pi /3}$ und dreht mit gleicher Geschwindigkeit wie das Signal $x_{2+}(t)$.

Hinweise:

Die Aufgabe gehört zum Kapitel Analytisches Signal und zugehörige Spektralfunktion.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$A$ =

$\text{V}$

$f_1$ =

$\text{kHz}$

$\varphi_1$ =

$\text{Grad}$

$f_2$ =

$\text{kHz}$

$\varphi_2$ =

$\text{Grad}$

$f_3$ =

$\text{kHz}$

$\varphi_3$ =

$\text{Grad}$

$t_1$ =

$\text{ms}$

$t_2$ =

$\text{ms}$

Musterlösung

Solution

1. Die Amplitude der harmonischen Schwingung ist gleich der Zeigerlänge. Für alle Signale gilt $A \; \underline{= 3 \ \text{V}}$.

2. Die gesuchte Frequenz ergibt sich zu $f_1 = \omega_1/(2\pi ) \; \underline{= 5 \ \text{kHz}}$. Die Phase kann aus $S_1 = 3 \ \text{V} \cdot \text{e}^{–\text{j} \cdot \varphi_1}$ ermittelt werden und ist $\varphi_1 \; \underline{= 0}$. Insgesamt ergibt sich

$$x_1(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$

3. Wegen $\omega_2 = 2\omega_1$ beträgt nun die Frequenz $f_2 = 2 \cdot f_1 \; \underline{= 10 \ \text{kHz}}$ . Die Phase ergibt sich mit dem Startzeitpunkt $S_2$ zu $\text{e}^{–\text{j} \cdot \varphi_2} = \text{j}$ ⇒ $\varphi_2 \; \underline{= –\pi /2 \; (–90^{\circ})}$. Somit lautet die Zeitfunktion:

$$x_2(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$

Dieses Signal ist somit „minus–sinusförmig”, was auch direkt am Zeigerdiagramm abgelesen werden kann:

Der Realteil von $x_{2+}(t)$ zum Zeitpunkt $t = 0$ ist 0. Da der Zeiger entgegen dem Uhrzeigersinn dreht, ergibt sich zunächst ein negativer Realteil.
Nach einer viertel Umdrehung ist $x_2(T/4) = - 3 \ \text{V}$. Dreht man nochmals in Schritten von $90^\circ$ entgegen dem Uhrzeigersinn weiter, so ergeben sich die Signalwerte $0 \ \text{V}$, $3 \ \text{V}$, und $0 \ \text{V}$.

4. Diese Teilaufgabe kann analog zu den Fragen 2) und 3) gelöst werden: $f_3 \; \underline{= 10 \ \text{kHz}}$, $\varphi_3 \; \underline{= 60^\circ}$.

5. Der Zeiger benötigt für eine Umdrehung genau die Periodendauer $T_3 = 1/f_3 \; \underline{= 0.1 \ \text{ms}} \;(= t_1)$.

6. Das analytische Signal startet bei $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}60^{\circ}}$. Dreht das Signal um $120^\circ$ weiter, so ergibt sich genau der gleiche Realteil. Es gilt dann mit $t_2 = t_1/3 \; \underline{= 0.033 \ \text{ms}} $ die folgende Beziehung:

$$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} .$$