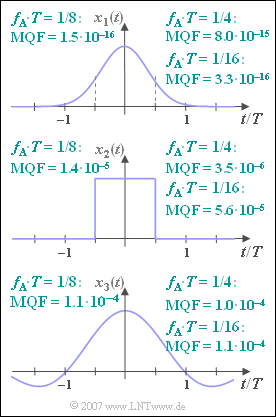
Exercise 5.3: Mean Square Error

Gaußimpuls, Rechteckimpuls, Spaltimpuls und einige Kenngrößen

Wir betrachten drei impulsartige Signale, nämlich

einen Gaußimpuls mit Amplitude $A$ und äquivalenter Dauer $T$:

$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$

einen Rechteckimpuls $x_2(t)$ mit Amplitude $A$ und Dauer $T$:

$$x_2(t) = \left\{ \begin{array}{c} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \hspace{0.05cm}, \\ \end{array}$$

einen so genannten Spaltimpuls gemäß nachfolgender Definition:

$$x_3(t) = A \cdot {\rm si}(\pi \cdot t/ T) ,\hspace{0.15cm}{\rm si}(x) = \sin(x)/x\hspace{0.05cm}.$$

Die Signalparameter seien $A = 1\ {\rm V}$ und $T = 1\ {\rm ms}$. Die konventionelle Fouriertransformation führt zu folgenden Spektralfunktionen:

$X_1(f)$ ist ebenfalls gaußförmig,
$X_2(f)$ verläuft entsprechend der si–Funktion,
$X_3(f)$ ist für $|f| < 1/(2 T$) konstant und außerhalb 0.

Für alle Spektralfunktionen gilt $X(f = 0) = A \cdot T$.

Ermittelt man das frequenzdiskrete Spektrum durch die Diskrete Fouriertransformation (DFT) mit den DFT-Parametern

$N = 512$ ⇒ Anzahl der berücksichtigten Abtastwerte im Zeit– und Frequenzbereich,
$f_{\rm A}$ ⇒ Stützstellenabstand im Frequenzbereich,

so wird dies aufgrund von Abbruch– und/oder Aliasingfehler zu Verfälschungen führen.

Die weiteren DFT–Parameter liegen mit $N$ und $f_{\rm A}$ eindeutig fest. Für diese gilt:

$$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm P}/N \hspace{0.05cm}.$$

Die Genauigkeit der jeweiligen DFT–Approximation wird durch den mittleren quadratischen Fehler (MQF) erfasst:

$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$

Die sich ergebenden MQF–Werte sind in obiger Grafik angegeben für $N = 512$ sowie für

$f_{\rm A} \cdot T = 1/4$,
$f_{\rm A} \cdot T = 1/8$,
$f_{\rm A} \cdot T = 1/16$.

Hinweise:

Die Aufgabe gehört zum Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Die Theorie zu diesem Kapitel ist im Lernvideo Fehlermöglichkeiten bei Anwendung der DFT zusammengefasst.

Fragebogen

Musterlösung

Solution

1. Mit den DFT–Parametern $N = 512$ und $f_{\rm A} \cdot T = 1/8$ folgt nach Multiplikation $$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$ Dadurch wird der Frequenzbereich $–f_{\rm P}/2 \leq f < f_{\rm P}/2$ erfasst: $f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$

2. Die Periodifizierung der Zeitfunktion basiert auf dem Parameter $T_{\rm P} = 1/f_{\rm A} = 8T$. Der Abstand zweier Abtastwerte beträgt somit

$$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$

3. Mit dieser Maßnahme wird gleichzeitig $T_{\rm P}$ von $8T$ auf $4T$ halbiert. Berücksichtigt werden somit nur noch Abtastwerte im Bereich $–2T \leq t < 2T$, was zu einer (geringfügigen) Erhöhung des Abbruchfehlers führt. Der mittlere quadratische Fehler (MQF) steigt dadurch beim Gaußimpuls $x_1(t)$ von $0.15 \cdot 10^{–15}$ auf $8 \cdot 10^{–15}$, obwohl der Aliasingfehler durch diese Maßnahme etwas kleiner wird.

4. Durch die Halbierung von $f_{\rm A}$ wird auch $f_{\rm P}$ halbiert. Dadurch erhöht sich der Aliasingfehler bei gleichzeitig kleinerem Abbruchfehler. Insgesamt steigt beim Gaußimpuls $x_1(t)$ der mittlere quadratische Fehler von $1.5 \cdot 10^{–16}$ auf $3.3 \cdot 10^{–16}$.

5. Wie aus der Grafik zu ersehen ist, trifft die letzte Aussage nicht zu im Gegensatz zu den ersten beiden. Aufgrund des langsamen, si–förmigen Abfalls der Spektralfunktion dominiert der Aliasingfehler. Der MQF–Wert ist bei $f_{\rm A} \cdot T = 1/8$ mit $1.4 \cdot 10^{–5}$ deshalb deutlich größer als beim Gaußimpuls ( $1.5 \cdot 10^{–16}$ ).

6. Die Spektralfunktion $X_3(f)$ hat hier einen rechteckförmigen Vorlauf, so dass die beiden ersten Aussagen nicht zutreffen. Dagegen ist bei dieser si–förmigen Zeitfunktion ein Abbruchfehler unvermeidbar. Dieser führt zu den angegebenen großen MQF–Werten ⇒ Lösungsvorschlag 3.

	Der Abbruchfehler wird vergrößert.
	Der Aliasingfehler wird vergrößert.

	MQF wird größer, da die Spektralfunktion $X_2(f)$ asymptotisch langsamer abfällt als $X_1(f)$.
	Es dominiert der Aliasingfehler.
	Es dominiert der Abbruchfehler.