Exercise 2.1Z: Which Tables Describe Groups?

Verschiedene Additionstabellen für $q = 3$

In dieser Aufgabe betrachten wir Mengen mit jeweils drei Elementen, allgemein bezeichnet mit $\{z_0, \, z_1, \, z_2\}$. Die Elemente können dabei sein:

Zahlen, beispielsweise $z_0 = 0, \ z_1 = 1, \ z_2 = 2$,
algebraische Ausdrücke wie $z_0 = A, \ z_1 = B, \ z_2 = C$,
irgendwas, beispielsweise $z_0 = „{\rm Apfel}”, \ z_1 = „{\rm Birne}”, \ z_2 = „{\rm Citrone}”$.

Eine Gruppe $(G, \ „+”)$ hinsichtlich der Addition ergibt sich dann, wenn durch eine Tabelle die „$+$”–Verknüpfung zwischen je zwei Elementen so definiert wurde, dass folgende Bedingungen erfüllt sind (die Laufvariablen $i, \ j, \ k$ können dabei jeweils die Werte $0, \ 1, \ 2$ annehmen):

Für alle $z_i ∈ G$ und $z_j ∈ G$ gilt $(z_i + z_j) ∈ G$ ⇒ Closure–Kriterium. Die Bedingung muss auch für $i = j$ erfüllt sein.
Für alle $z_i, \ z_j, \ z_k$ gilt $(z_i + z_j) + z_k = z_i + (z_j + z_k)$ ⇒ Assoziativgesetz.
Es gibt ein hinsichtlich Addition neutrales Element $N_{\rm A} ∈ G$, so dass für alle $z_i ∈ G$ gilt: $z_i + N_{\rm A} = z_i$.
Für alle $z_i ∈ G$ gibt es ein hinsichtlich Addition inverses Element ${\rm Inv}_{\rm A}(z_i) ∈ G$, so dass $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A}$ gilt.

Wird zudem für alle $z_i ∈ G$ und $z_j ∈ G$ noch das Kommutativgesetz ⇒ $z_i + z_j = z_j + z_i$ erfüllt, so spricht man von einer kommutativen Gruppe oder – nach dem norwegischen Mathematiker Niels Hendrik Abel – von einer abelschen Gruppe.

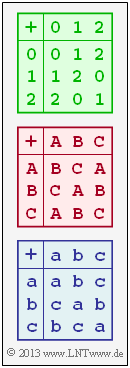
Die Zahlenmenge $\{0, \, 1, \, 2\}$ ist eine abelsche (kommutative) Gruppe. Entsprechend der grün umrandeten Additionstabelle in obiger Grafik ist hier die Addition modulo $3$ zu verstehen. Somit ist auch die Summe stets $0, \ 1$ oder $2$. Das neutrale Element ist $N_{\rm A} = 0$ und das zu $z_i$ inverse Element ${\rm Inv}_{\rm A}(z_i) = -z_i$:

$${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0.1cm}{\rm Inv_A}(1) = (-1)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 2 \hspace{0.05cm},\hspace{0.1cm}{\rm Inv_A}(2) = (-2)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 1 \hspace{0.05cm}.$$

In dieser Aufgabe sollen Sie überprüfen, ob auch die beiden weiteren in der obigen Grafik dargestellten Additionstabellen jeweils zu einer algebraischen Gruppe gehören.

Hinweise:

Die Aufgabe gehört zum Kapitel Einige Grundlagen der Algebra.
Bezug genommen wird insbesondere auf die Seite Definition und Beispiele einer algebraischen Gruppe.

Fragebogen

	Das neutrale Element ist $N_{\rm A} = {\rm C}$.
	Die Inversen sind $\rm Inv_A(A) = B, \ Inv_A(B) = A, \ Inv_A(C) = C$.
	Es handelt sich hier um eine additive Gruppe $(G, \ +)$.
	Auch die Bedingung einer abelschen Gruppe wird erfüllt.

	Ja.
	Nein.

	Das neutrale Element ist $N_{\rm A} = a$.
	Die additiven Inversen sind $\rm Inv_A(a) = a, \ Inv_A(b) = b, \ Inv_A(c) = c$.
	Es handelt sich um eine abelsche Gruppe.

Musterlösung

Solution

(1) Es treffen alle Aussagen zu. Das neutrale Element $N_{\rm A} = {\rm C}$ erkennt man aus der letzten Zeile der Additionstabelle. Aus der Bedingung $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A} = {\rm C}$ erhält man:

$\rm Inv_A(A) = B$, da an der zweiten Stelle der ersten Zeile das einzige $\rm C$ steht,
$\rm Inv_A(B) = A$, da an der ersten Stelle der zweiten Zeile das einzige $\rm C$ steht,
$\rm Inv_A(C) = C$, da an der letzten Stelle der dritten Zeile das einzige $\rm C$ steht.

Das Assoziativgesetz überprüfen wir (unzulässigerweise) nur an einem einzigen Beispiel. Durch zweimalige Anwendung der Additionstabelle erhält man beispielsweise $\rm (A + B) + C = C + C$. Das gleiche Ergebnis ergibt sich für $\rm A + (B + C) = A + B = C$.

Damit sind alle Bedingungen für eine additive Gruppe erfüllt. Die Gültigkeit des Kommutativgesetzes erkennt man aus der Symmetrie der Additionstabelle zur Diagonalen. Damit ist die Gruppe auch abelsch.

Übrigens: Die (rote) Additionstabelle ergibt sich aus der grünen Tabelle durch die Umbenennungen $0 → \rm C, \ 1 → A$ und $2 → \rm B$ und anschließender $\rm ABC$–Sortierung.

(2) Richtig ist Nein. Alle Aussagen sind allein durch die Additionstabelle bestimmt und nicht durch die Bedeutung der Elemente. Auch der Autor dieser Aufgabe kann allerdings nicht tiefergehend begründen, warum die Modulo–3–Addition von „$\rm Apfel$” und „$\rm Birne$” das neutrale Element „$\rm Zitrone$” ergibt.

(3) Die beiden ersten Aussagen treffen zu im Gegensatz zur letzten. Das Kommutativgesetz wird verletzt (keine Symmetrie bezüglich der Tabellendiagonalen). Beispielsweise gilt:

$$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$

$${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$

$${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$

Damit ist die hier betrachtete Verknüpfung keine abelsche (kommutative) Gruppe. Mehr noch, wegen der Verletzung des Assoziativgesetzes liegen hier auch die Grundvoraussetzungen einer Gruppe nicht vor. Beispielsweise gilt:

$${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$

$$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$