Exercise 5.7: OFDM Transmitter using IDFT
From LNTwww
Blockschaltbild der IDFT
In dieser Aufgabe wird ein OFDM–Sender genauer betrachtet, der mit Hilfe der Inversen Diskreten Fouriertransformation (IDFT) realisiert ist. Dabei gelte:
- Das System habe $N = 4$ Träger.
- Die Rahmendauer sei $T_{\ \rm R} = 0.25 \ \rm ms$.
- Ein Guard–Intervall wird nicht verwendet.
- In jedem Rahmen werden $16$ Bit übertragen.
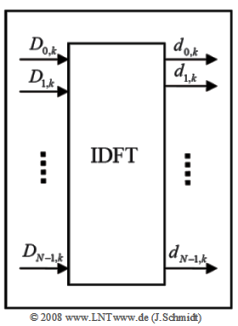
- Die rechte obere Grafik zeigt den Block „IDFT„ der OFDM–Senderstruktur.
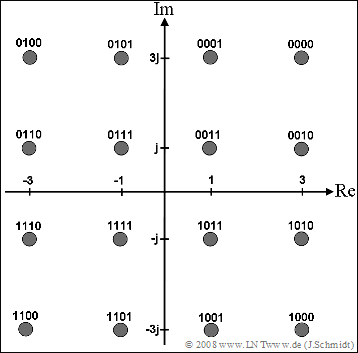
- Jeweils vier Bit ergeben hierbei ein komplexes Symbol gemäß der unten links skizzierten 16–QAM–Signalraumzuordung.
Vorgeschlagene 16–QAM-Signalraumzuordnung
Hinweise:
- Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
- Bezug genommen wird auch auf das Kapitel Diskrete Fouriertransformation.
- Die Gleichung der IDFT lautet mit $ν = 0$, ... , $N–1$:
- $$\quad d_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu ,k} \cdot w^{ - \nu \cdot \mu } } \quad {\rm{mit}} \quad w = {\rm{e}}^{ - {\rm{j}} {\rm{2\pi}}/N}.$$
Fragebogen
Musterlösung
(1) Da hier kein Guard–Intervall berücksichtigt wird, ist die Symboldauer $T$ gleich der Rahmendauer $T_{\rm{R}} = 0.25 \ \rm ms$. Bei $N = 4$ Trägern und 16–QAM gilt für die Bitrate am Eingang:
- $$R_{\rm{B}} = \frac{1}{T_{\rm{B}}} = \frac{4 \cdot {\rm{log}_2}\hspace{0.08cm}(16)}{T} = \frac{4 \cdot 4}{0.25\,\,{\rm ms}}\hspace{0.15cm}\underline {= 64\,\,{\rm kbit/s}}.$$
(2) Aus der Signalraumzuordnung folgt für die Trägerkoeffizienten (auf den Index k wird verzichtet):
- $${\rm{Bitfolge}}\hspace{0.2cm}1111:\hspace{0.5cm} D_0 = -1 - {\rm{j}}\hspace{0.4cm}\Rightarrow\hspace{0.3cm}{\rm Re}[D_0]\hspace{0.15cm}\underline{=-1},\hspace{0.2cm}{\rm Im}[D_0]\hspace{0.15cm}\underline{=-1},$$
- $${\rm{Bitfolge}}\hspace{0.2cm}0111:\hspace{0.5cm} D_1 = -1 + {\rm{j}}\hspace{0.4cm}\Rightarrow\hspace{0.3cm}{\rm Re}[D_1]\hspace{0.15cm}\underline{=-1},\hspace{0.2cm}{\rm Im}[D_1]\hspace{0.15cm}\underline{=+1},$$
- $${\rm{Bitfolge}}\hspace{0.2cm}1000:\hspace{0.5cm} D_2 = +3 - 3{\rm{j}},\hspace{0.15cm}\Rightarrow\hspace{0.3cm}{\rm Re}[D_2]\hspace{0.15cm}\underline{=+3},\hspace{0.2cm}{\rm Im}[D_2]\hspace{0.15cm}\underline{=-3},$$
- $${\rm{Bitfolge}}\hspace{0.2cm}0000:\hspace{0.5cm} D_3 = +3 + 3{\rm{j}}\hspace{0.2cm}\Rightarrow\hspace{0.3cm}{\rm Re}[D_3]\hspace{0.15cm}\underline{=+3},\hspace{0.2cm}{\rm Im}[D_3]\hspace{0.15cm}\underline{=+3}.$$
(3) Die angegebene IDFT–Gleichung lautet mit $N = 4$:
- $$d_{\nu } = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu } \cdot {\rm{e}}^{ \hspace{0.04cm} {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} \pi/2 \hspace{0.04cm}\cdot \hspace{0.04cm}\nu \hspace{0.04cm}\cdot \hspace{0.04cm} \mu } } .$$
Daraus erhält man für $ν = 0$, ... , $3$:
- $$d_0 = D_0 + D_1 +D_2 +D_3 = 4 \hspace{2.9cm}\Rightarrow\hspace{0.4cm}{\rm Re}[d_0]\hspace{0.15cm}\underline{=4},\hspace{0.2cm}{\rm Im}[d_0]\hspace{0.15cm}\underline{=0},$$
- $$d_1 = D_0 + {\rm{j}} \cdot D_1 - D_2 -{\rm{j}} \cdot D_3 = -2 + 2 \cdot {\rm{j}}\hspace{0.4cm}\Rightarrow\hspace{0.4cm}{\rm Re}[d_1]\hspace{0.15cm}\underline{=-2},\hspace{0.2cm}{\rm Im}[d_1]\hspace{0.15cm}\underline{=+2},$$
- $$d_2 = D_0 - D_1 + D_2 - D_3 = -8 \cdot {\rm{j}}\hspace{2.1cm}\Rightarrow\hspace{0.4cm}{\rm Re}[d_2]\hspace{0.15cm}\underline{=0},\hspace{0.2cm}{\rm Im}[d_2]\hspace{0.15cm}\underline{=-8},$$
- $$d_3 = D_0 - {\rm{j}} \cdot D_1 - D_2 +{\rm{j}} \cdot D_3 = -6 + 6 \cdot {\rm{j}}\hspace{0.4cm}\Rightarrow\hspace{0.4cm}{\rm Re}[d_3]\hspace{0.15cm}\underline{=-6},\hspace{0.2cm}{\rm Im}[d_3]\hspace{0.15cm}\underline{=+6}.$$
(4) Richtig sind die beiden letzten Lösungsvorschläge:
- Bei OFDM ist der Crest–Faktor eher groß.
- Dies kann bei den verwendeten Verstärkerschaltungen zu Problemen in Bezug auf Linearitätsanforderungen und Energieeffizienz führen.
