Exercise 1.6: Root Nyquist System
From LNTwww
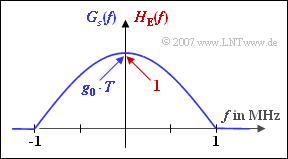
Die nebenstehende Grafik zeigt
- das Spektrum $G_{s}(f)$ des Sendegrundimpulses,
- den Frequenzgang $H_{\rm E}(f)$ des Empfangsfilters
eines binären und bipolaren Übertragungssystems, die zueinander formgleich sind:
- $$G_s(f) = \left\{ \begin{array}{c} A \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}, \\ \end{array}$$
- $$H_{\rm E }(f) = \left\{ \begin{array}{c} 1 \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}. \\ \end{array}$$
In der gesamten Aufgabe gelte $A = 10^{–6} \ \rm V/Hz$ und $f_{2} = 1 \ \rm MHz$.
- Unter der Voraussetzung, dass die Bitrate $R = 1/T$ richtig gewählt wird, erfüllt der Detektionsgrundimpuls $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$ das erste Nyquistkriterium.
- Bei der dazugehörigen Spektralfunktion $G_{d}(f)$ erfolgt dabei der Flankenabfall cosinusförmig ähnlich einem Cosinus–Rolloff–Spektrum.
- Der Rolloff–Faktor $r$ ist in dieser Aufgabe zu ermitteln.
Hinweise:
- Die Aufgabe gehört zum Kapitel Optimierung der Basisbandübertragungssysteme.
- Zahlenwerte der Q–Funktion liefert zum Beispiel das interaktive Applet Komplementäre Gaußsche Fehlerfunktionen.
- Der Crestfaktor ist der Qotient aus Maximalwert und Effektivwert des Sendesignals und damit ein Maß für die sendeseitigen Impulsinterferenzen:
- $$C_{\rm S} = \frac{s_0}{\sqrt{E_{\rm B}/T}} = \frac{{\rm Max}[s(t)]}{\sqrt{{\rm E}[s^2(t)]}}= {s_0}/{s_{\rm eff}}.$$
Fragebogen
Musterlösung
(1) Mit den Funktionen $G_{s}(f)$ und $H_{\rm E}(f)$ gilt für das Spektrum des Detektionsgrundimpulses für $|f| \leq f_{2}$:
- $$G_d(f) = G_s(f) \cdot H_{\rm E}(f) = A \cdot \cos^2 \left( \frac {\pi \cdot f}{2 \cdot f_2} \right).$$
- Nach der allgemeinen Definition des Cosinus–Rolloff–Spektrums ergeben sich die Eckfrequenzen $f_{1} = 0$ und $f_{2} = 1\ \rm MHz$.
- Daraus folgt für die Nyquistfrequenz (Symmetriepunkt bezüglich des Flankenabfalls):
- $$f_{\rm Nyq} = \frac{f_1 +f_2 } {2 } \hspace{0.1cm}\underline { = 0.5\,{\rm MHz}}\hspace{0.05cm}.$$
- Der Rolloff–Faktor beträgt
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.1cm}\underline {= 1} \hspace{0.05cm}.$$
- Das bedeutet: $G_{d}(f)$ beschreibt ein $\cos^{2}$–Spektrum.
(2) Der Zusammenhang zwischen Nyquistfrequenz und Symboldauer $T$ lautet $f_{\rm Nyq} = 1/(2T)$.
- Daraus folgt für die Bitrate $R = 1/T = 2 \cdot f_{\rm Nyq}\ \underline{= 1 \ \rm Mbit/s}$.
- Beachten Sie die unterschiedlichen Einheiten für Frequenz und Bitrate.
(3) Die erste und die dritte Lösungsalternative sind zutreffend:
- Es handelt es sich um ein optimales Binärsystem unter der Nebenbedingung der Leistungsbegrenzung.
- Der Crestfaktor ist bei Leistungsbegrenzung nicht von Bedeutung. Bei den hier gegebenen Voraussetzungen würde $C_{\rm S} > 1$ gelten.
(4) Die Bitfehlerwahrscheinlichkeit eines optimalen Systems kann wie folgt berechnet werden:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$
- Im vorliegenden Beispiel erhält man für die mittlere Energie pro Bit:
- $$E_{\rm B} = \ \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = A^2 \cdot \int_{-1/T}^{+1/T} H_{\rm Nyq}(f) \,{\rm d} f = \ \frac {A^2}{T} = \frac {(10^{-6}\,{\rm V/Hz})^2}{10^{-6}\,{\rm s}} = 10^{-6}\,{\rm V^2s}\hspace{0.05cm}.$$
- Mit $N_{0} = 8 \cdot 10^{–8} \ \rm V^{2}/Hz$ ergibt sich daraus weiter:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot 10^{-6}\,{\rm V^2s}}{8 \cdot 10^{-8}\,{\rm V^2/Hz}}}\right)= {\rm Q} \left( \sqrt{25}\right)= {\rm Q} (5) \hspace{0.1cm}\underline {= 0.287 \cdot 10^{-6}}\hspace{0.05cm}.$$