Zur Erzeugung von Walsh-Funktionen (neues Applet)
Contents
Programmbeschreibung
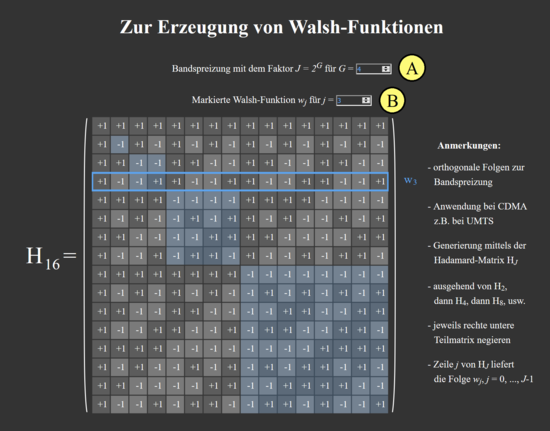
Dieses Applet ermöglicht die Darstellung der Hadamard-Matrizen HJ zur Konstruktion der Walsh-Funktionen wj. Dabei können der Faktor J der Bandspreizung sowie die Markierung der einzelnen Walsh-Funktionen (durch blaue Umrandung der Zeilen der Matrix) verändert werden.
Theoretischer Hintergrund
Anwendung
Die Walsh-Funktionen sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS.
- Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen (periodische KKF) stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar. Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null.
- Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe Aufgabe 5.4.
- Hinsichtlich PAKF (periodische AKF) sind diese Folgen weniger gut: Jede einzelne Walsh–Funktion hat eine andere PAKF und jede einzelne PAKF ist ungünstiger als bei einer vergleichbaren PN–Sequenz. Das bedeutet: Die Synchronisierung ist bei Walsh–Funktionen schwieriger als mit PN–Sequenzen.
Konstruktion
Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der Hadamard-Matrizen erfolgen. Eine Hadamard-Matrix HJ der Ordnung J ist eine J×J-Matrix, die zeilenweise die ±1-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt J=2G für eine natürliche Zahl G. Ausgehend von H1=(+1) und
H2=(+1+1+1−1)
gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen:
H2N=(+HN+HN+HN−HN)
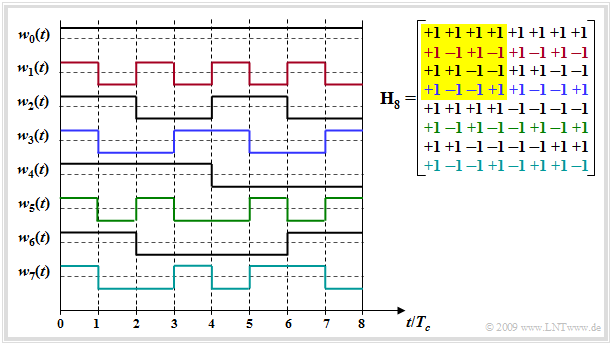
Die Grafik zeigt die Hadamard–Matrix H8 (rechts) und die damit J−1 konstruierbaren Spreizfolgen.
- J−1 deshalb, da die ungespreizte Folge w0(t) meist nicht verwendet wird.
- Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen wj(t).
- Die Matrix H4 ist gelb hinterlegt.
Material, das Sie eventuell noch verwenden könnten
Spreizfolgen mit sehr günstigen PKKF–Eigenschaften sind die so genannten Walsh–Funktionen, deren Konstruktion auf der Hadamard–Matrix basiert und durch Rekursion in einfacher Weise durchführbar ist. Ausgehend von der Matrix H2 können weitere Hadamard–Matrizen H2J wie folgt generiert werden:
- H2=[+1+1+1−1]⇒H2J=[HJHJHJ−HJ]⇒H4=[+1+1+1+1+1−1+1−1+1+1−1−1+1−1−1+1].
Die J Zeilen einer solchen Matrix beschreiben die J möglichen Spreizfolgen (jeweils der Länge J), die mit w0(t) bis w_{J–1}(t) durchnummeriert werden.
Die Grafik zeigt die Hadamard–Matrix \mathbf H_8 (rechts) und die damit J -1 konstruierbaren Spreizfolgen.
- J - 1 deshalb, da die ungespreizte Folge w_0(t) meist nicht verwendet wird.
- Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen w_j(t).
- Die Matrix \mathbf H_4 ist gelb hinterlegt.
Die Animation Zur Erzeugung von Walsh–Funktionen zeigt den Konstruktionsalgorithmus solcher Folgen. Weiter gilt:
- Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null. Somit sind Walsh–Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA–System aufgrund ihrer Orthogonalität optimale Spreizfolgen.
- Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe Aufgabe 5.4.
- Hinsichtlich PAKF (periodische AKF) sind diese Folgen weniger gut: Jede einzelne Walsh–Funktion hat eine andere PAKF und jede einzelne PAKF ist ungünstiger als bei einer vergleichbaren PN–Sequenz. Das bedeutet: Die Synchronisierung ist bei Walsh–Funktionen schwieriger als mit PN–Sequenzen.
Zur Handhabung des Applets
(A) Auswahl des Faktors zur Bandspreizung als Zweierpotenz von G
(B) Auswahl der jeweiligen Walsh-Funktion w_j
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2007 von Thomas Großer im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018/2019 wurde das Programm von Marwen Ben Ammar und Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.
