Exercise 2.1Z: Which Tables Describe Groups?

Additionstabellen für $q = 3$

In dieser Aufgabe betrachten wir Mengen mit jeweils drei Elementen, allgemein bezeichnet mit $\{z_0, \, z_1, \, z_2\}$. Die Elemente können dabei sein:

Zahlen, beispielsweise $z_0 = 0, \ z_1 = 1, \ z_2 = 2$,
algebraische Ausdrücke wie $z_0 = A, \ z_1 = B, \ z_2 = C$,
irgendwas, beispielsweise $z_0 = \ „\hspace{-0.05cm}{\rm Apfel}\hspace{0.05cm}”, \ z_1 = \ „\hspace{-0.05cm}{\rm Birne}\hspace{0.05cm}”, \ z_2 = \ „\hspace{-0.05cm}{\rm Citrone}\hspace{0.05cm}”$.

Eine Gruppe $(G, \ „+”)$ hinsichtlich der Addition ergibt sich dann, wenn durch eine Tabelle die „$+$”–Verknüpfung zwischen je zwei Elementen so definiert wurde, dass folgende Bedingungen erfüllt sind (die Laufvariablen $i, \ j, \ k$ können dabei jeweils die Werte $0, \ 1, \ 2$ annehmen):

Für alle $z_i ∈ G$ und $z_j ∈ G$ gilt $(z_i + z_j) ∈ G$ ⇒ Closure–Kriterium. Die Bedingung muss auch für $i = j$ erfüllt sein.
Für alle $z_i, \ z_j, \ z_k$ gilt $(z_i + z_j) + z_k = z_i + (z_j + z_k)$ ⇒ Assoziativgesetz.
Es gibt ein hinsichtlich Addition neutrales Element ⇒ $N_{\rm A} ∈ G$, so dass für alle $z_i ∈ G$ gilt: $z_i + N_{\rm A} = z_i$.
Für alle $z_i ∈ G$ gibt es ein hinsichtlich Addition inverses Element ⇒ ${\rm Inv}_{\rm A}(z_i) ∈ G$, so dass $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A}$ gilt.

Wird zudem für alle $z_i ∈ G$ und $z_j ∈ G$ noch das Kommutativgesetz ⇒ $z_i + z_j = z_j + z_i$ erfüllt, so spricht man von einer kommutativen Gruppe oder – nach dem norwegischen Mathematiker Niels Hendrik Abel – von einer Abelschen Gruppe.

Die Zahlenmenge $\{0, \, 1, \, 2\}$ ist eine Abelsche (kommutative) Gruppe.

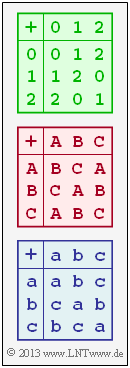
Entsprechend der grün umrandeten Additionstabelle in obiger Grafik ist hier die Addition modulo $3$ zu verstehen.
Somit ist auch die Summe stets $0, \ 1$ oder $2$.
Das neutrale Element ist $N_{\rm A} = 0$ und das zu $z_i$ inverse Element ${\rm Inv}_{\rm A}(z_i) = -z_i$:

$${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(1) = (-1)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 2 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(2) = (-2)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 1 \hspace{0.05cm}.$$

In dieser Aufgabe sollen Sie überprüfen, ob auch die beiden weiteren in der obigen Grafik dargestellten Additionstabellen jeweils zu einer algebraischen Gruppe gehören.

Hinweise:

Die Aufgabe gehört zum Kapitel Einige Grundlagen der Algebra.
Bezug genommen wird insbesondere auf die Seite Definition und Beispiele einer algebraischen Gruppe.

Fragebogen

	Das neutrale Element ist $N_{\rm A} = {\rm C}$.
	Die Inversen sind $\rm Inv_A(A) = B, \ \ Inv_A(B) = A, \ \ Inv_A(C) = C$.
	Es handelt sich hier um eine additive Gruppe $(G, \ +)$.
	Auch die Bedingung einer Abelschen Gruppe wird erfüllt.

	Ja.
	Nein.

	Das neutrale Element ist $N_{\rm A} = a$.
	Die additiven Inversen sind $\rm Inv_A(a) = a, \ \ Inv_A(b) = b, \ \ Inv_A(c) = c$.
	Es handelt sich um eine Abelsche Gruppe.

Musterlösung

Solution

(1) Es treffen alle Aussagen zu:

Das neutrale Element $N_{\rm A} = {\rm C}$ erkennt man aus der letzten Zeile der Additionstabelle.
Aus der Bedingung $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A} = {\rm C}$ erhält man:

$\rm Inv_A(A) = B$, da an der zweiten Stelle der ersten Zeile das einzige $\rm C$ steht,
$\rm Inv_A(B) = A$, da an der ersten Stelle der zweiten Zeile das einzige $\rm C$ steht,
$\rm Inv_A(C) = C$, da an der letzten Stelle der dritten Zeile das einzige $\rm C$ steht.

Das Assoziativgesetz überprüfen wir (unzulässigerweise) nur an einem einzigen Beispiel. Durch zweimalige Anwendung der Additionstabelle erhält man beispielsweise $\rm (A + B) + C = C + C=C$. Das gleiche Ergebnis ergibt sich für $\rm A + (B + C) = A + B = C$.

Damit sind alle Bedingungen für eine additive Gruppe erfüllt. Die Gültigkeit des Kommutativgesetzes erkennt man aus der Symmetrie der Additionstabelle zur Diagonalen. Damit ist die Gruppe auch „abelsch”.

Übrigens: Die (rote) Additionstabelle ergibt sich aus der grünen Tabelle durch die Umbenennungen $0 → \rm C, \ 1 → A$ und $2 → \rm B$ und anschließender $\rm ABC$–Sortierung.

(2) Richtig ist Nein:

Alle Aussagen sind allein durch die Additionstabelle bestimmt und nicht durch die Bedeutung der Elemente.
Auch der Autor dieser Aufgabe kann allerdings nicht tiefergehend begründen, warum die Modulo–3–Addition von „$\rm Apfel$” und „$\rm Birne$” das neutrale Element „$\rm Citrone$” ergibt.

(3) Die beiden ersten Aussagen treffen zu im Gegensatz zur letzten:

Das Kommutativgesetz wird verletzt (keine Symmetrie bezüglich der Tabellendiagonalen). Beispielsweise gilt:

$$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$

$${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$

$${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$

Damit ist die hier betrachtete Verknüpfung keine Abelsche (kommutative) Gruppe.
Mehr noch, wegen der Verletzung des Assoziativgesetzes liegen hier bereits die Grundvoraussetzungen einer Gruppe nicht vor. Beispielsweise gilt:

$${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$

$$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$