Exercise 4.08: Repetition to the Convolutional Codes

Zustandsübergangsdiagramm eines nichtrekursiven Codes

Die Turbocodes basieren auf Faltungscodes, die im Kapitel Grundlagen der Faltungscodierung auführlich behandelt werden.

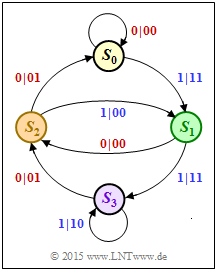
Ausgehend vom nebenstehenden Zustandsübergangsdiagramm sollen wesentliche Eigenschaften und Kenngrößen des betrachteten Rate–$1/2$–Faltungscodes ermittelt werden, wobei wir ausdrücklich auf folgende Theorieseiten verweisen:

Im Zustandsübergangsdiagramm wird grundsätzlich vom Zustand $S_0$ ausgegangen. Von jedem Zustand gehen zwei Pfeile ab. Die Beschriftung lautet „$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$”. Bei einem systematischen Code gilt dabei:

Das erste Codebit ist identisch mit dem Informationsbit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$
Das zweite Codebit ist das Prüfbit (Paritybit): $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$.

Hinweise:

Die Aufgabe bezieht sich auf das Kapitel Grundlegendes zu den Turbocodes.
In den Fragen zu dieser Aufgabe werden folgende semi–infinite Vektoren verwendet:

Informationssequenz $\ \underline{u} = (u_1, \, u_2, \text{ ...})$,
Paritysequenz $\ \underline{p} = (p_1, \, p_2, \text{ ...})$,
Impulsantwort $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \text{ ...})$.

Fragebogen

Musterlösung

Solution

(1) Richtig ist der Lösungsvorschlag 2:

Die Impulsantwort $\underline{g}$ ist gleich der Ausgangsfolge $\underline{p}$ für die Eingangsfolge $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$.
Ausgehend vom Zustand $S_0$ ergeben sich im Zustandsübergangsdiagramm folgende Übergänge:

$$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm Impulsantwort} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$

Für ein nichtrekursives Filter mit Gedächtnis $m$ gilt $g_i ≡ 0$ für $i > m$. In unserem Beispiel ist $m = 2$.
Der Lösungsvorschlag 1 gilt dagegen für das rekursive Filter (RSC) entsprechend der Aufgabe 4.9.

(2) Es sei $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ und $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Dann gilt für die Paritysequenz aufgrund der Linearität:

$$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0 ,\hspace{0.05cm} 0,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...})= $$

$$\ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...}\hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) $$

$$\Rightarrow \hspace{0.3cm}\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.$$

Richtig sind also die Lösungsvorschläge 1 und 2 im Gegensatz zur Antwort 3:

Für $u_7 = 1$ gilt $p_7 = 1, \ p_8 = 0, \ p_9 = 1$ und $p_i ≡ 0$ für $i > 9$.

(3) Richtig ist der Lösungsvorschlag 2:

Aus dem Zustandsübergangsdiagramm erkennt man die Codeparameter $k = 1$ und $n = 2$.
Das heißt: Die Übertragungsfunktionsmatrix $\mathbf{G}(D)$ besteht aus zwei Elementen ⇒ der Vorschlag 3 ist falsch.
Die erste Komponente von $\mathbf{G}(D)$ ist tatsächlich 1, da ein systematischer Code vorliegt: $\ \underline{x}^{(1)} ≡ \underline{z}$.
Die zweite Komponente von $\mathbf{G}(D)$ ist gleich der $D$–Transformierten der Impulsantwort $\underline{g}$, wobei die Dummy–Variable $D$ eine Verzögerung um ein Bit angibt:

$$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$

Über die Fragestellung hinausgehend betrachten wir hier auch noch die vorliegende Filterstruktur:

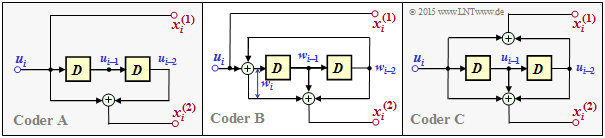
Drei Beispiele für Rate–1/2–Faltungscodierer

In der Grafik ist der hier betrachtete Coder als Coder $\rm A$ links dargestellt.

Dieser ist ebenso wie der Coder $\rm B$ systematisch, und
basiert im Gegensatz zu Coder $\rm B$ aber auf einem nichtrekursiven Filter.
Der Coder $\rm C$ hat ebenfalls eine nichtrekursive Struktur, ist aber nicht systematisch.
Die äquivalente systematische Repräsentation von Coder $\rm C$ ist der Coder $\rm B$.

(4) Richtig sind die Lösungsvorschläge 2 und 3:

Die Aufgabe könnte in gleicher Weise gelöst werden wie die Teilaufgabe (2).
Wir wählen hier aber zur Abwechslung den Weg über die $D$–Transformation:

$$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D^2 + D^5$$

$$\Rightarrow \hspace{0.3cm} P(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} U(D) \cdot G(D) = (1+ D^2 + D^5) \cdot (1+ D^2 ) =1+ D^2 + D^5 + D^2 + D^4 + D^7 = 1+ D^4 + D^5 + D^7$$

$$\Rightarrow \hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})\hspace{0.05cm}.$$

(5) Die freie Distanz $d_{\rm F}$ eines Faltungscoders ist gleich der Anzahl der Bits, durch die sich zwei beliebigen Sequenzen dieses Codes mindestens unterscheiden.

Gehen wir wie allgemein üblich als Bezugsgröße von der Nullsequenz $\underline{0} \ \Rightarrow \ S_0 → S_0 → S_0 → S_0 → \ \text{ ...} \ $ aus, so ergibt sich $d_{\rm F}$ gleichzeitig als das minimale Hamming–Gewicht (Anzahl der Einsen) einer zulässigen Codesequenz $\underline{x} ≠ \underline{0}$.

Aus dem Zustandsübergangsdiagramm erkennt man, dass die freie Distanz zum Beispiel durch den Pfad

$$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$

gekennzeichnet ist, also durch die Codesequenz $00 \hspace{0.1cm} 11 \hspace{0.1cm} 00 \hspace{0.1cm} 01 \hspace{0.1cm} 00 \text{ ...} \ .$

Dementsprechend gilt für die freie Distanz dieses nichtrekursiven Codes: $\hspace{0.2cm} d_{\rm F} \ \underline{= 3}$.

	Es gilt $\underline{g} = (1, \, 1, \,1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \text{ ...})$.
	Es gilt $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{ ...})$.

	Die ersten sechs Bit der Paritysequenz sind „$1, \, 0, \, 1, \, 1, \, 0, \, 1$”.
	Mit $u_7 = 0$ gilt $p_i = 0$ für $i > 6$.
	Mit $u_7 = 1$ gilt $p_i = 0$ für $i > 8$.

	Es gilt $\mathbf{G}(D) = \big [1, \ 1 + D \big ]$.
	Es gilt $\mathbf{G}(D) = \big [1, \ 1 + D^2 \big ]$.
	Es gilt $\mathbf{G}(D) = \big [1 + D^2 \big ]$.

	Die ersten acht Bit der Parityfolge sind „$1, \, 0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0$”.
	Die ersten acht Bit der Parityfolge sind „$1, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1$”.
	Es gilt $p_i = 0$ für $i ≥ 9$.