Exercise 3.9: Conditional Mutual Information

• Return to book

Ergebnis  $W$  als Funktion
von  $X$,  $Y$,  $Z$

Wir gehen von den statistisch unabhängigen Zufallsgrößen  $X$,  $Y$  und  $Z$  mit den folgenden Eigenschaften aus:

$$X \in \{1,\ 2 \} \hspace{0.05cm},\hspace{0.35cm} Y \in \{1,\ 2 \} \hspace{0.05cm},\hspace{0.35cm} Z \in \{1,\ 2 \} \hspace{0.05cm},\hspace{0.35cm} P_X(X) = P_Y(Y) = \big [ 1/2, \ 1/2 \big ]\hspace{0.05cm},\hspace{0.35cm}P_Z(Z) = \big [ p, \ 1-p \big ].$$

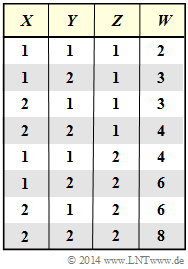
Aus  $X$,  $Y$  und  $Z$  bilden wir die neue Zufallsgröße  $W = (X+Y) \cdot Z$.

• Es ist offensichtlich, dass es zwischen  $X$  und  $W$  statistische Abhängigkeiten gibt   ⇒   Transinformation  $I(X; W) ≠ 0$.
• Außerdem wird auch  $I(Y; W) ≠ 0$  sowie  $I(Z; W) ≠ 0$  gelten, worauf in dieser Aufgabe jedoch nicht näher eingegangen wird.

In dieser Aufgabe werden drei verschiedene Transinformationsdefinitionen verwendet:

• die herkömmliche  Transinformation zwischen  $X$  und  $W$:

$$I(X;W) = H(X) - H(X|\hspace{0.05cm}W) \hspace{0.05cm},$$

• die bedingte  Transinformation zwischen  $X$  und  $W$  bei gegebenem Festwert  $Z = z$:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}|\hspace{0.05cm} Z = z) - H(X|\hspace{0.05cm}W ,\hspace{0.05cm} Z = z) \hspace{0.05cm},$$

• die bedingte  Transinformation zwischen  $X$  und  $W$  bei gegebener Zufallsgröße  $Z$:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}|\hspace{0.05cm} Z ) - H(X|\hspace{0.05cm}W \hspace{0.05cm} Z ) \hspace{0.05cm}.$$

Der Zusammenhang zwischen den beiden letzten Definitionen lautet:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z ) = \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.2cm} P_Z(z) \cdot I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = z)\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Verschiedene Entropien zweidimensionaler Zufallsgrößen.
• Insbesondere wird auf die Seite  Bedingte Transinformation Bezug genommen .

Fragebogen

1

Wie groß ist die Transinformation zwischen  $X$  und  $W$,  falls stets  $Z = 1$  gilt?

$I(X; W | Z = 1) \ = \ $ $\ \rm bit$

2

Wie groß ist die Transinformation zwischen  $X$  und  $W$,  falls stets  $Z = 2$  gilt?

$I(X; W | Z = 2) \ = \ $ $\ \rm bit$

3

Nun gelte  $p = {\rm Pr}(Z = 1)$.  Wie groß ist die bedingte Transinformation zwischen  $X$  und  $W$, falls  $z \in Z = \{1,\ 2\}$  bekannt ist?

$p = 1/2\text{:} \ \ \ I(X; W | Z) \ = \ $ $\ \rm bit$

$p = 3/4\text{:} \ \ \ I(X; W | Z) \ = \ $ $\ \rm bit$

4

Wie groß ist die unkonditionierte Transinformation für  $p = 1/2$?

$I(X; W) \ = \ $ $\ \rm bit$

Musterlösung

Solution

2D-Wahrscheinlichkeitsfunktionen für  $Z = 1$

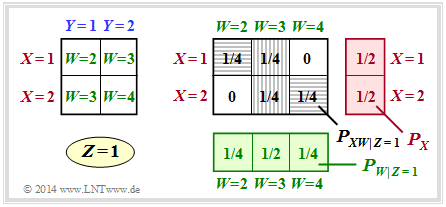
(1)  Die obere Grafik gilt für  $Z = 1$   ⇒   $W = X + Y$. 

• Unter den Voraussetzungen  $P_X(X) = \big [1/2, \ 1/2 \big]$  sowie  $P_Y(Y) = \big [1/2, \ 1/2 \big]$  ergeben sich somit die Verbundwahrscheinlichkeiten  $P_{ XW|Z=1 }(X, W)$  entsprechend der rechten Grafik (graue Hinterlegung).

• Damit gilt für die Transinformation unter der festen Bedingung  $Z = 1$:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 1) \hspace{-0.05cm} = \hspace{-1.1cm}\sum_{(x,w) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XW}\hspace{0.01cm}|\hspace{0.01cm} Z\hspace{-0.03cm} =\hspace{-0.03cm} 1)} \hspace{-1.1cm} P_{XW\hspace{0.01cm}|\hspace{0.01cm} Z\hspace{-0.03cm} =\hspace{-0.03cm} 1} (x,w) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{XW\hspace{0.01cm}|\hspace{0.01cm} Z\hspace{-0.03cm} =\hspace{-0.03cm} 1} (x,w) }{P_X(x) \cdot P_{W\hspace{0.01cm}|\hspace{0.01cm} Z\hspace{-0.03cm} =\hspace{-0.03cm} 1} (w) }$$

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 1) = 2 \cdot \frac{1}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/2 \cdot 1/4} + 2 \cdot \frac{1}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/4}{1/2 \cdot 1/2}$$

$$\Rightarrow \hspace{0.3cm} I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 1) \hspace{0.15cm} \underline {=0.5\,{\rm (bit)}} \hspace{0.05cm}.$$

• Der erste Term fasst die beiden horizontal schraffierten Felder in der Grafik zusammen, der zweite Term die vertikal schraffierten Felder.
• Letztere liefern wegen  $\log_2 (1) = 0$  keinen Beitrag.

2D-Wahrscheinlichkeitsfunktionen für  $Z = 2$

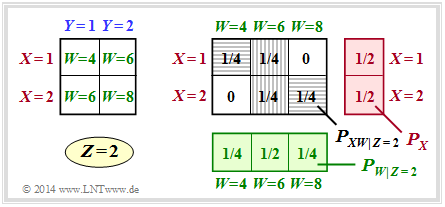
(2)  Für  $Z = 2$  gilt zwar $W = \{4,\ 6,\ 8\}$, es ändert sich aber hinsichtlich der Wahrscheinlichkeitsfunktionen gegenüber der Teilaufgabe  (1)  nichts.

• Demzufolge erhält man auch die gleiche bedingte Transinformation:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 2) = I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 1) \hspace{0.15cm} \underline {=0.5\,{\rm (bit)}} \hspace{0.05cm}.$$

(3)  Die Gleichung lautet für  $Z = \{1,\ 2\}$  mit  ${\rm Pr}(Z = 1) =p$  und  ${\rm Pr}(Z = 2) =1-p$:

$$I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z) = p \cdot I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 1) + (1-p) \cdot I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z = 2)\hspace{0.15cm} \underline {=0.5\,{\rm (bit)}} \hspace{0.05cm}.$$

• Es ist berücksichtigt, dass nach den Teilaufgaben  (1)  und  (2)  die bedingten Transinformationen für gegebenes  $Z = 1$  und gegebenes  $Z = 2$  gleich sind.
• Damit ist  $I(X; W|Z)$, also unter der Bedingung einer stochastischen Zufallsgröße  $Z = \{1,\ 2\}$  mit  $P_Z(Z) = \big [p, \ 1 – p\big ]$  unabhängig von  $p$.
• Das Ergebnis gilt insbesondere auch für  $\underline{p = 1/2}$  und  $\underline{p = 3/4}$.

Zur Berechnung der Verbundwahrscheinlichkeit für $XW$

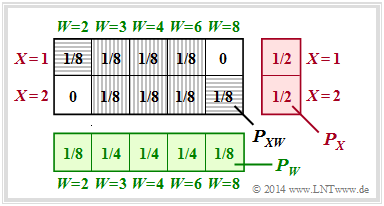
(4)  Die Verbundwahrscheinlichkeit  $P_{ XW }$  hängt von den  $Z$–Wahrscheinlichkeiten  $p$  und  $1 – p$  ab.

• Für  $Pr(Z = 1) = Pr(Z = 2) = 1/2$  ergibt sich das rechts skizzierte Schema.
• Zur Transinformation tragen nur wieder die beiden horizontal schraffierten Felder bei:

$$I(X;W) = 2 \cdot \frac{1}{8} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/8}{1/2 \cdot 1/8} \hspace{0.15cm} \underline {=0.25\,{\rm (bit)}} \hspace{0.35cm} < \hspace{0.35cm} I(X;W \hspace{0.05cm}|\hspace{0.05cm} Z) \hspace{0.05cm}.$$

Das Ergebnis  $I(X; W|Z) > I(X; W)$  trifft für dieses Beispiel, aber auch für viele andere Anwendungen zu:

• Kenne ich  $Z$, so weiß ich mehr über die 2D–Zufallsgröße  $XW$  als ohne diese Kenntnis.
• Man darf dieses Ergebnis aber nicht verallgemeinern:

Manchmal gilt tatsächlich  $I(X; W) > I(X; W|Z)$, so wie im  Beispiel 3 im Theorieteil.