Das Gram-Schmidt-Verfahren

Programmbeschreibung

Das Applet verdeutlicht das Gram–Schmidt–Verfahren. Dieses ermöglicht, eine Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale mit Hilfe von $N \le M$ orthonormalen Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ in folgender Form darzustellen:

$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$

Der vektorielle Repräsentant der Musterfunktion $s_1(t)$ lautet dann: $$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$

Das Applet zeigt alle Grafiken, die zum Verständnis des Gram–Schmidt–Verfahrens erforderlich sind, und als jeweiliges Ergebnis

die 2D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=2$,
die 3D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=3$.

Theoretischer Hintergrund

Signaldarstellung mit orthonormalen Basisfunktionen

Wir gehen von einer Menge $\{s_i(t)\}$ möglicher Sendesignale aus, die den möglichen Nachrichten $m_i$ eineindeutig zugeordnet sind. Mit $i = 1$, ... , $M$ gelte:

$$m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: \hspace{0.3cm} m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.$$

Für das Folgende setzen wir weiter voraus, dass die $M$ Signale $s_i(t)$ energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.

$\text{Satz:}$ Eine jede Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale lässt sich in $N \le M$ orthonormale Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ entwickeln. Es gilt:

$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$

Jeweils zwei Basisfunktionen $\varphi_j(t)$ und $\varphi_k(t)$ müssen orthonormal zueinander sein, das heißt, dass gelten muss $(\delta_{jk}$ nennt man das Kronecker–Symbol$)$:

$$<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.4cm}j = k\hspace{0.1cm} \\ {\rm falls}\hspace{0.4cm} j \ne k \hspace{0.1cm}\\ \end{array} \hspace{0.05cm}.$$

Der Parameter $N$ gibt dabei an, wieviele Basisfunktionen $\varphi_j(t)$ benötigt werden, um die $M$ möglichen Sendesignale darzustellen. Mit anderen Worten: $N$ ist die Dimension des Vektorraums, der von den $M$ Signalen aufgespannt wird. Dabei gilt:

Ist $N = M$, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien $E_i = \ <\hspace{-0.01cm}s_i(t), \hspace{0.05cm}s_i(t) \hspace{-0.01cm}>$ können durchaus ungleich Eins sein.
Der Fall $N < M$ ergibt sich, wenn mindestens ein Signal $s_i(t)$ als Linearkombination von Basisfunktionen $\varphi_j(t)$ dargestellt werden kann, die sich bereits aus anderen Signalen $s_j(t) \ne s_i(t)$ ergeben haben.

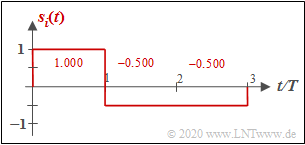
Darstellung der drei Sendesignale durch zwei Basisfunktionen

$\text{Beispiel 1:}$ Wir betrachten $M = 3$ energiebegrenzte Signale gemäß der Grafik.

Man erkennt sofort:

Die Signale $s_1(t)$ und $s_2(t)$ sind zueinander orthogonal.

Die Energien sind $E_1 = A^2 \cdot T = E$ und $E_2 = (A/2)^2 \cdot T = E/4$.

Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sind jeweils formgleich mit $s_1(t)$ bzw. $s_2(t)$.
Beide Signale besitzen jeweils die Energie „Eins”:

$$\varphi_1(t)=\frac{s_1(t)}{\sqrt{E_1} } = \frac{s_1(t)}{\sqrt{A^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_1(t)}{A}$$

$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},$$

$$\varphi_2(t) =\frac{s_2(t)}{\sqrt{E_2} } = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T} } = \frac{1}{\sqrt{ T} } \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}$$

$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = {\sqrt{E} }/{2}\hspace{0.05cm}.$$

Das Signal $s_3(t)$ kann durch die vorher bestimmten Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ ausgedrückt werden:

$$s_3(t) =s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},$$

$$\hspace{0.5cm}\Rightarrow \hspace{0.1cm} s_{31} = {A}/{2} \cdot \sqrt {T}= {\sqrt{E} }/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.$$

Trotz $M=3$ gilt also im vorliegenen Fall nur $N=2$.

Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ als Achsen dargestellt, wobei $E = A^2 \cdot T$ gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist.

Die vektoriellen Repräsentanten der Signale $s_1(t)$, $s_2(t)$ und $s_3(t)$ in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:

$$\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.5cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.5cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.$$

Das Verfahren nach Gram-Schmidt

Im letzten $\text{Beispiel}$ war die Bestimmung der beiden orthonormalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sehr einfach, da diese formgleich mit $s_1(t)$ bzw. $s_2(t)$ waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_N(t)$ für beliebig vorgebbare Signale $s_1(t)$, ... , $s_M(t)$, und zwar wie folgt:

Die erste Basisfunktion $\varphi_1(t)$ ist stets formgleich mit $s_1(t)$. Es gilt:

$$\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.$$

$\text{Hinweise zur Nomenklatur:}$

(1) Ausgehend von zwei reellen und energiebegrenzten Zeitfunktionen $x(t)$ und $y(t)$ erhält man für das innere Produkt allgemein:

$$<\hspace{-0.01cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.01cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm}.$$

(2) Daraus ergibt sich die Euklidische Norm der Zeitfunktion $s_1(t)$:

$$\vert \vert s_1(t) \vert \vert = \sqrt{<\hspace{-0.01cm}s_1(t), \hspace{0.15cm}s_1(t) \hspace{-0.01cm}>} $$

Es wird nun angenommen, dass aus den Signalen $s_1(t)$, ... , $s_{k-1}(t)$ bereits die Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ berechnet wurden $(n \le k)$.

Dann berechnen wir mittels der nächsten Funktion $s_k(t)$ die Hilfsfunktion

$$\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{kj} = \hspace{0.01cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.01cm} >, \hspace{0.2cm} j = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm}, n-1\hspace{0.05cm}.$$

Hat diese Hilfsfunktion die Norm $||\theta_k(t)|| = 0$, so liefert $s_k(t)$ keine neue Basisfunktion. Vielmehr lässt sich dann $s_k(t)$ durch die $n-1$ bereits vorher gefundenen Basisfunktionen $\varphi_1(t)$, ... , $\varphi_{n-1}(t)$ ausdrücken:

$$s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.$$

Eine neue Basisfunktion (nämlich die $n$–te) ergibt sich nur für den Fall $||\theta_k(t)|| \ne 0$:

$$\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.$$

Diese Prozedur wird solange fortgesetzt, bis alle $M$ Signale berücksichtigt wurden.

Danach hat man alle $N \le M$ orthonormalen Basisfunktionen $\varphi_j(t)$ gefunden.
Der Sonderfall $N = M$ ergibt sich nur dann, wenn alle $M$ Signale linear voneinander unabhängig sind.

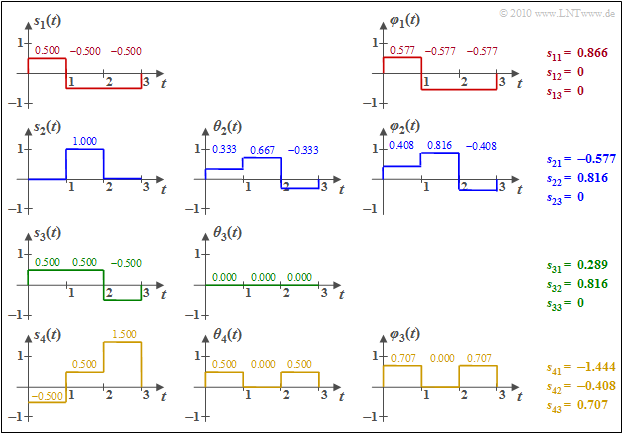
$\text{Beispiel 2:}$ Wir betrachten die $M = 4$ energiebegrenzten Signale $s_1(t)$, ... , $s_4(t)$ entsprechend der Grafik. Zur Vereinfachung der Berechnungen sind hier sowohl die Amplituden als auch die Zeit normiert.

Zum Gram-Schmidt-Verfahren

Man erkennt aus diesen Skizzen:

Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$. Wegen $E_1 = \vert \vert s_1(t) \vert \vert ^2 = 3 \cdot 0.5^2 = 0.75$ ergibt sich $s_{11} = \vert \vert s_1(t) \vert \vert = 0.866$. $\varphi_1(t)$ selbst besitzt abschnittsweise die Werte $\pm 0.5/0.866 = \pm0.577$.

Zur Berechnung der Hilfsfunktion $\theta_2(t)$ berechnen wir

$$s_{21} = \hspace{0.1cm} < \hspace{-0.01cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.01cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577$$

$$ \Rightarrow \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, \hspace{0.15cm} 0.667, \hspace{0.15cm} -0.333) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\vert \vert \theta_2(t) \vert \vert^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667$$

$$ \Rightarrow \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.3cm} \varphi_2(t) = \theta_2(t)/s_{22} = (0.408, \hspace{0.15cm} 0.816, \hspace{0.15cm} -0.408)\hspace{0.05cm}. $$

Die inneren Produkte zwischen $s_1(t)$ mit $\varphi_1(t)$ bzw. $\varphi_2(t)$ liefern folgende Ergebnisse:

$$s_{31} \hspace{0.01cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289,$$

$$s_{32} \hspace{0.1cm} = \hspace{0.01cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.01cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816$$

$$\Rightarrow \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.$$

Das bedeutet: Die grüne Funktion $s_3(t)$ liefert keine neue Basisfunktion $\varphi_3(t)$, im Gegensatz zur Funktion $s_4(t)$. Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.

Die verschiedenen Rubriken bei der Auswahl der Programmparameter

Das Programm bietet insgesamt $4 \cdot 6 = 24$ Möglichkeiten zur Einstellung der jeweiligen Menge $\{s_i(t)\}$ möglicher Sendesignale. Diese $24$ Parametersätze sind in vier Rubriken eingeteilt. Die vier Rubriküberschriften treffen den Sachverhalt nicht hundertprozentig und sind deshalb in Hochkommata gesetzt:

(1) Rubrik „Basisband” ⇒ gültig für die Einstellungen $\rm (A)$ ... $\rm (F)$:

Signalform bei „Basisband”

Jedes Mustersignal $s_i(t)$ besteht aus drei Rechteckfunktionen unterschiedlicher Höhen und jeweiliger Dauer $T$.
Die einzelnen Rechteckhöhen sind Vielfache von $\pm 0.25$ und die gesamte Signaldauer ergibt $3T$.
Mit dem seitlichen Slider kann man das Signal $s_i(t)$ um Vielfache von $\pm 0.25$ nach oben und unten verschieben.
Solche Signale treten zum Beispiel bei der binären oder mehrstufigen Basisbandübertragung auf.
Im $\text{Beispiel 2}$ des hier angegebenen Links erkennt man zum Beispiel die grafischen Darstellungen

eines binären Signals $q(t)$,
eines ternären Signals $s_3(t)$,
eines quaternären Signals $s_4(t)$.

(2) Rubrik „M–ASK / BPSK” ⇒ gültig für die Einstellungen $\rm (G)$ ... $\rm (L)$:

Signalform bei „M–ASK / BPSK”

Die Mustersignale $s_i(t)$ haben ebenfalls die Dauer $3T$ und sind ähnlich aufgebaut wie bei der Rubrik (1).
Im Unterschied zu (1) wird jede Rechteckfunktion $($Dauer $T)$ durch eine Periode einer Sinusfunktionen ersetzt.
Der angegebene Zahlenwert gibt hier die Amplitude des sinusförmigen Teilstücks an.
Bei negativem Vorzeichen wird aus dem „Sinus” die Funktion „Minus–Sinus”.
Mit dem seitlichen Slider kann man die Amplitude von $s_i(t)$ um Vielfache von $\pm 0.25$ vergrößern oder verkleinern.
Solche Signale können zum Beispiel bei der M–ASK (mehrstufiges Amplitude Shift Keying) auftreten, ebenso bei BPSK (Binary Phase Shift Keying).

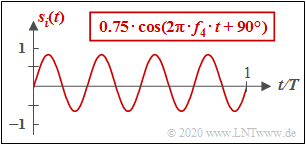
(3) Rubrik „Nur eine Frequenz” ⇒ gültig für die Einstellungen $\rm (M)$ ... $\rm (R)$:

Signalform bei „Nur eine Frequenz”

Alle Mustersignale $s_i(t)$ haben die Dauer $T$ und sind jeweils Harmonische Schwingungen der Form

$$s_i(t) = A \cdot \cos(2\pi \cdot f \cdot t + \phi)\hspace{0.3cm}\text{mit}\hspace{0.3cm}f=f_k.$$

Der Parameter $k$ gibt die Anzahl der Schwingungen innerhalb der Periodendauer $T$ an.
Die Grafik gilt für: $A=0.75, \hspace{0.3cm}f= f_4 =4/T \hspace{0.3cm}\Rightarrow\hspace{0.3cm}k=4, \hspace{0.3cm}\phi= -90^\circ$ ⇒ sinusförmiger Verlauf.
Die Eigenschaft „Nur eine Frequenz” bezieht sich auf die einzelnen Mustersignale $s_i(t)$. Die $M$ Signalformen eines Sets können durchaus unterschiedliche Frequenzen $f$ aufweisen.
Mit dem Slider lässt sich die Phase von $s_i(t)$ um Vielfache von $\pm 22.5^\circ$ in beide Richtungen variieren.
Solche Harmonische haben für alle (analogen und digitalen) Nachrichtensysteme große Bedeutung.

(4) Rubrik „Mehrere Frequenzen” ⇒ gültig für die Einstellungen $\rm (S)$ ... $\rm (X)$:

Es gelten ähnliche Voraussetzungen wie für die „Rubrik 3”, es sind aber nun stets mehrere Frequenzen beteiligt.
Die Eigenschaft „Mehrere Frequenzen” bezieht sich auf einzelne Mustersignale $s_i(t)$ oder auch auf den gesamten Set $\{s_i(t)\}$.
Möglich sind somit auch Mustersignale der folgenden Form $($mit $k=0$ ⇒ $f=f_0 = k/T = 0$ ⇒ Gleichsignal$)$:

$$s_i(t) = 1 \cdot \cos(2\pi \cdot f_0 \cdot t) - 0.5 \cdot \cos(2\pi \cdot f_2 \cdot t)-0.5 \cdot \cos(2\pi \cdot f_3 \cdot t).$$

Der Parameter $k$ muss auch nicht ganzzahlig sein. Beispielsweise kennzeichnet $k= 4.5$ viereinhalb Schwingunen Schwingungen innerhalb der Zeitdauer $T$.
Mit dem Slider können die Frequenzkenngrößen $k$ um Vielfache von $0.25$ vergrößert oder verkleinert werden.

Versuchsdurchführung

Noch anpassen

Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
Lösung nach Drücken von „Musterlösung”.

Die Nummer 0 entspricht einem „Reset”:

Gleiche Einstellung wie beim Programmstart.
Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.

Bis hierher

(1) Es gilt die Einstellung $\rm A$. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”.

Einstellung $\rm A$ beschreibt das $\text{Beispiel 2}$ im Theorieteil. Die Basisfunktion $\varphi_1(t)$ ist identisch mit dem Signal $s_1(t)$, aber mit Signalenergie $E=1$.
Es gibt hier nur $N=3$ Basisfunktionen, da die Hilfsfunktion $\theta_3(t)$ identisch Null ist.
Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ können im 3D–Vektorraum abgelesen werden; Beispiel: $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.

(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.

Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$.

(3) Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?

Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$, $\varphi_2(t) = s_2(t)$, $\varphi_3(t) = s_3(t)$.

(4) Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.

Es gilt $s_3(t) = s_1(t)/4 - s_2(t)/2$ und $s_4(t) = -s_1(t) - s_2(t)$. Das heißt: $s_3(t)$ und $s_4(t)$ liefern keine neuen Basisfunktionen.

(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$.

Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$.
Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).

(6) Welches Ergebnis liefern die vier Signale gemäß der Einstellung $\rm F$?

Die die Signale $s_1(t)$, ... , $s_4(t)$ basieren alle auf einer einzigen Basisfunktion $\varphi_1(t)$, die formgleich mit $s_1(t)$ ist. Es gilt $N=1$.
Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ sind $\pm 0.866$ und $\pm 1.732$. Sie liegen alle auf einer Linie.

(7) Es gilt nun die „M–ASK / BPSK”–Einstellung $\rm G$. Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen.

Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm A$.
Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor $\sqrt{2}$ aus.
Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (-1.021, \hspace{0.15cm} -0.289, \hspace{0.15cm} +0.500)$ anstelle von $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
Bei der Einstellung $\rm H$ sind gegenüber $\rm G$ alle Amplituden verdoppelt. Somit ergibt sich hier $\mathbf{s}_4 = (-2.041, \hspace{0.15cm} -0.577, \hspace{0.15cm} +1.000)$.

(8) Es gelte die „M–ASK / BPSK”–Einstellung $\rm I$. Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.

Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm C$, aber nun mit nur halb so großen Energien.
Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$.
Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$.
Ebenso wird mit der „M–ASK / BPSK”–Einstellung $\rm J$ eine ähnliche Konstellation betrachtet wie mit der „Basisband”–Einstellung $\rm D$. Gleiches gilt für $\rm K$ und $\rm E$.

(9) Es gelte die „M–ASK / BPSK”–Einstellung $\rm L$. Interpretieren Sie das Ergebnis. Gibt es einen Zusammenhang zu einer früheren Aufgabe?

?????.

(10) Es gelte die „Nur eine Frequenz”–Einstellung $\rm M$. Interpretieren Sie die dargestellten Grafiken.

Alle Signale $s_i(t)$ haben die Amplitude $A_i = 1$ und die Frequenz $f=f_0$. Die Phasen sind $\phi_1 = +45^\circ$, $\phi_2 = -135^\circ$, $\phi_3 = +135^\circ$ und $\phi_4 = -45^\circ$.
Die $M=4$ Signale lassen sich durch nur $N=2$ Basisfunktionen ausdrücken. Dies gilt für (fast) alle Einstellungen der dritten Rubrik.
Die Basisfunktion $\varphi_1(t)$ ist formgleich mit $s_1(t)$ und $\varphi_2(t)$ formgleich mit $s_2(t)$. Auch dies gilt für die meisten Einstellungen der dritten Rubrik.

(11) Wählen Sie die Einstellungen $M=4 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ und variieren Sie $f_{\rm G}/R_{\rm B}$. Interpretieren Sie die Ergebnisse.

$f_{\rm G}/R_{\rm B}=0.48$ führt zur minimalen Fehlerwahrscheinlichkeit $p_{\rm U} \approx 0.21\%$. Kompromiss zwischen $ö_{\rm norm}= 0.312$ und $\sigma_{\rm norm}= 0.109$.
Bei zu kleiner Grenzfrequenz dominieren die Impulsinterferenzen. Beispiel: $f_{\rm G}/R_{\rm B}= 0.3$: $ö_{\rm norm}= 0.157; $ $\sigma_{\rm norm}= 0.086$ ⇒ $p_{\rm U} \approx 3.5\%$.
Bei zu großer Grenzfrequenz dominiert das Rauschen. Beispiel: $f_{\rm G}/R_{\rm B}= 1.0$: $ö_{\rm norm}= 0.333; $ $\sigma_{\rm norm}= 0.157$ ⇒ $p_{\rm U} \approx 1.7\%$.
Aus dem Vergleich mit (9) erkennt man: Bei Quaternärcodierung ist es günstiger, Impulsinterferenzen zuzulassen.

(12) Welche Unterschiede zeigt das Auge für $M=3 \text{ (AMI-Code), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ gegenüber dem vergleichbaren Binärsystem? Interpretation.

Der Detektionsgrundimpuls $g_d(t)$ ist in beiden Fällen gleich. Die Abtastwerte sind jeweils $g_0 = 0.771, \ g_1 = 0.114$.
Beim AMI–Code gibt es zwei Augenöffnungen mit je $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$. Beim Binärcode: $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$.
Die AMI–Folge besteht zu 50% aus Nullen. Die Symbole $+1$ und $-1$ wechseln sich ab ⇒ es gibt keine lange $+1$–Folge und keine lange $-1$–Folge.
Darin liegt der einzige Vorteil des AMI–Codes: Dieser kann auch bei einem gleichsignalfreien Kanal ⇒ $H_{\rm K}(f= 0)=0$ angewendet werden.

(13) Gleiche Einstellung wie in (12), zudem $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Analysieren Sie die Fehlerwahrscheinlichkeit des AMI–Codes.

Trotz kleinerem $\sigma_{\rm norm} = 0.103$ hat der AMI–Code eine höhere Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2\%$ als der Binärcode: $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
Für $f_{\rm G}/R_{\rm B}<0.34$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ ⇒ $p_{\rm U} =50\%$. Beim Binärcode: Für $f_{\rm G}/R_{\rm B}>0.34$ ist das Auge geöffnet.

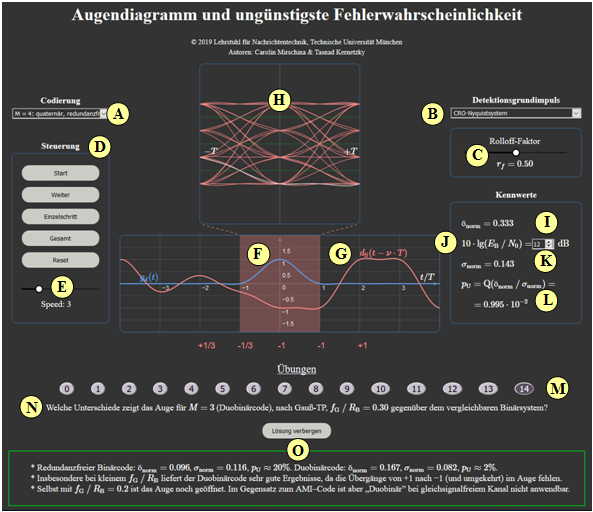
(14) Welche Unterschiede zeigt das Auge für $M=3 \text{ (Duobinärcode), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.30$ gegenüber dem vergleichbaren Binärsystem?

Redundanzfreier Binärcode: $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\% $ Duobinärcode: $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\% $.
Insbesondere bei kleinem $f_{\rm G}/R_{\rm B}$ liefert der Duobinärcode gute Ergebnisse, da die Übergänge von $+1$ nach $-1$ (und umgekehrt) im Auge fehlen.
Selbst mit $f_{\rm G}/R_{\rm B}=0.2$ ist das Auge noch geöffnet. Im Gegensatz zum AMI–Code ist aber „Duobinär” bei gleichsignalfreiem Kanal nicht anwendbar.

Zur Handhabung des Applets

(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)

(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}

(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)

(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)

(E) Geschwindigkeit der Augendiagrammdarstellung

(F) Darstellung: Detektionsgrundimpuls $g_d(t)$

(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$

(H) Darstellung: Augendiagramm im Bereich $\pm T$

( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)

(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)

(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)

(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)

(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl

(N) Bereich für die Versuchsdurchführung: Aufgabenstellung

(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2008 von Thomas Großer im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab