Korrelation und Regressionsgerade

Open Applet in a new tab

Theoretischer Hintergrund

Erwartungswerte von 2D–Zufallsgrößen und Korrelationskoeffizient

Wir betrachten eine zweidimensionale  $\rm (2D)$–Zufallsgröße  $(X,\ Y)$  mit der Wahrscheinlichkeitsdichtefunktion  $\rm (WDF)$  $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten  $X$  und  $Y$  statistische Abhängigkeiten bestehen.  Ein Sonderfall ist die Korrelation.

$\text{Definition:}$  Unter  Korrelation  versteht man eine lineare Abhängigkeit  zwischen den Einzelkomponenten  $X$  und  $Y$.

• Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
• Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.

Für das Folgende setzen wir voraus, dass  $X$  und  $Y$  mittelwertfrei seien   ⇒   ${\rm E}\big [ X \big ] = {\rm E}\big [ Y \big ]=0$.  Zur Beschreibung der Korrelation genügen dann folgende Erwartungswerte:

• die  Varianzen  in  $X$–  bzw. in  $Y$–Richtung:

$$\sigma_X^2= {\rm E}\big [ X^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}x^2 \cdot f_{X}(x) \, {\rm d}x\hspace{0.05cm},\hspace{0.5cm}\sigma_Y^2= {\rm E}\big [Y^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}y^2 \cdot f_{Y}(y) \, {\rm d}y\hspace{0.05cm};$$

• die  Kovarianz  zwischen den Einzelkomponenten  $X$  und  $Y$:

$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\ \cdot y \cdot f_{XY}(x,y) \, {\rm d}x\, {\rm d}y\hspace{0.05cm}.$$

Bei statististischer Unabhängigkeit der beiden Komponenten  $X$  und  $Y$  ist die Kovarianz  $\mu_{XY} \equiv 0$. 

• Das Ergebnis  $\mu_{XY} = 0$  ist auch bei statistisch abhängigen Komponenten  $X$  und  $Y$  möglich, nämlich dann, wenn diese unkorreliert, also  linear unabhängig  sind.
• Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung  $Y=X^2.$

Man spricht dann von  vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen  $X$  und  $Y$  durch die Gleichung  $Y = K · X$  ausgedrückt wird.

Dann ergibt sich für die Kovarianz:

• $\mu_{XY} = σ_X · σ_Y$  bei positivem Wert von  $K$,
• $\mu_{XY} = -σ_X · σ_Y$  bei negativem  $K$–Wert.

Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.

$\text{Definition:}$  Der  Korrelationskoeffizient  ist der Quotient aus der Kovarianz  $\mu_{XY}$  und dem Produkt der Effektivwerte  $σ_X$  und  $σ_Y$  der beiden Komponenten:

$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}.$$

Der Korrelationskoeffizient  $\rho_{XY}$  weist folgende Eigenschaften auf:

• Aufgrund der Normierung gilt stets  $-1 \le ρ_{XY} ≤ +1$.
• Sind die beiden Zufallsgrößen  $X$  und  $Y$  unkorreliert, so ist  $ρ_{XY} = 0$.
• Bei strenger linearer Abhängigkeit zwischen  $X$  und  $Y$  ist  $ρ_{XY}= ±1$   ⇒   vollständige Korrelation.
• Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem  $X$–Wert im statistischen Mittel auch  $Y$  größer ist als bei kleinerem  $X$.
• Dagegen drückt ein negativer Korrelationskoeffizient aus, dass  $Y$  mit steigendem  $X$  im Mittel kleiner wird.

2D-WDF  $f_{XY}(x, y)$  sowie die zugehörigen Randwahrscheinlichkeitsdichten  $f_{X}(x)$  und  $f_{Y}(y)$

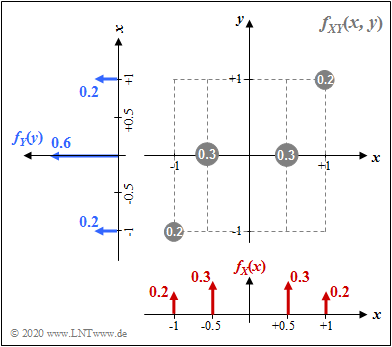
$\text{Beispiel 1:}$  Die 2D–Zufallsgröße  $(X,\ Y)$  sei diskret und kann nur vier verschiedene Werte annehmen:

• $(+0.5,\ 0)$  sowie $(-0.5,\ 0)$  jeweils mit der Wahrscheinlichkeit  $0.3$,
• $(+1,\ +\hspace{-0.09cm}1)$  sowie $(-1,\ -\hspace{-0.09cm}1)$  jeweils mit der Wahrscheinlichkeit  $0.2$.

$\rm (A)$  Die Varianzen bzw. die Streuungen können aus   $f_{X}(x)$  und  $f_{Y}(y)$  berechnet werden:

$$\sigma_X^2 = 2 \cdot \big [0.2 \cdot 1^2 + 0.3 \cdot 0.5^2 \big] = 0.55\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_X = 0.7416,$$

$$\sigma_Y^2 = \big [0.2 \cdot (-1)^2 + 0.6 \cdot 0^2 +0.2 \cdot (+1)^2 \big] = 0.4\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_Y = 0.6325.$$

$\rm (B)$  Für die Kovarianz ergibt sich der folgende Erwartungswert:

$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = 2 \cdot \big [0.2 \cdot 1 \cdot 1 + 0.3 \cdot 0.5 \cdot 0 \big] = 0.4.$$

$\rm (C)$  Damit erhält man für den Korrelationskoeffizient:

$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}=\frac{0.4 } {0.7416 \cdot 0.6325 }\approx 0.8528.$$

Regressionsgerade

Gaußsche 2D-WDF mit Korrelationsgerade

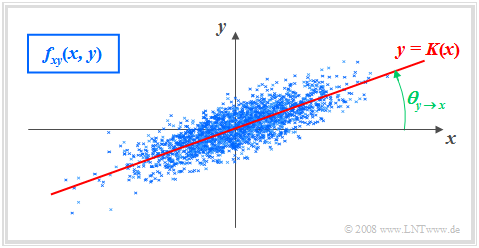
Ziel der linearen Regression ist es, einen einfachen (linearen) Zusammenhang zwischen zwei Zufallsgrößen  $X$  und  $Y$  zu anzugeben, deren $\text{2D-WDF}$  $f_{XY}(x, y)$  durch Punkte  $(x_1, y_1 )$  ...  $(x_N, y_N )$  in der  $(x,\ y)$–Ebene vorgegeben ist. Die Skizze zeigt das Prinzip am Beispiel mittelwertfreier Größen:  Gesucht ist die Gleichung der Geraden  $K$  ⇒   $y=c_{\rm opt} \cdot x$  mit der Eigenschaft, dass der mittlere quadratische (Euklidische) Abstand  $\rm (MQA)$  aller Punkte von dieser Geraden minimal ist. Man bezeichnet diese Gerade auch als  Korrelationsgerade. Diese kann als eine Art  „statistische Symmetrieachse“  interpretiert werden.

Bei einer großen Datenmenge  $N$  ist der mathematische Aufwand beträchtlich, den bestmöglichen Parameter  $C = c_{\rm opt}$  zu ermitteln. Der Aufwand wird deutlich reduziert, wenn man den Abstand nur in  $x$– oder in  $y$–Richtung definiert.

$\text{(a)}\hspace{0.5cm} \text{Regressionsgerade }R_{y \to x}$     (rote Gerade in der App)

Der $y$–Wert wird auf den $x$–Wert zurückgeführt, was in etwa einer der möglichen Bedeutungen „Zurückfallen” des Wortes „Regression” entspricht.

• Geradengleichung,  Winkel  $\theta_{y \to x}$  der Geraden  $R_{y \to x}$  zur   $x$–Achse:

$$y=C_{y \to x} \cdot x \ \ \text{mit} \ \ C_{y \to x}=\frac{\sigma_Y}{\sigma_X}\cdot\rho_{XY}= \frac{\mu_{XY}}{\sigma_X^2},\hspace{0.6cm} \theta_{y \to x}={\rm arctan}\ (C_{y \to x}).$$

• Kriterium:     Der mittlere Abstand aller Punkte  $(x_n, y_n )$  von der Regressionsgeraden $R_{y \to x}$  in  $y$–Richtung ist minimal:

$${\rm MQA}_Y = {\rm E} \big [ y_n - C_{y \to x} \cdot x_n\big ]^2 = \frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_n - C_{y \to x} \cdot x_n\big ]^{\rm 2}={\rm Minimum}.$$

Die zweite Gleichung gilt nur, wenn alle Punkte  $(x_n, y_n )$  der 2D–WDF gleichwahrscheinlich sind.

$\text{(b)}\hspace{0.5cm} \text{Regressionsgerade }R_{x \to y}$     (blaue Gerade in der App)

Die Regression in Gegenrichtung – also von  $x$  auf  $y$ – bedeutet dagegen, dass der $x$–Wert auf den $y$–Wert zurückgeführt wird und sich für  ${\rm MQA}_y$  der minimale Wert ergibt.

• Geradengleichung,  Winkel  $\theta_{x \to y}$  der Geraden  $R_{x \to y}$  zur   $x$–Achse:

$$y=C_{x \to y} \cdot x \ \ \text{mit} \ \ C_{x \to y}=\frac{\sigma_X}{\sigma_Y}\cdot\rho_{XY}= \frac{\mu_{XY}}{\sigma_Y^2},\hspace{0.6cm} \theta_{x \to y}={\rm arctan}\ (C_{x \to y}).$$

• Kriterium:     Der mittlere Abstand aller Punkte  $(x_n, y_n )$  von der Regressionsgeraden $R_{x \to y}$  in  $x$–Richtung ist minimal:

$${\rm MQA}_X = {\rm E} \big [ x_n - y_n/C_{x \to y}\big ]^2 = \frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [x_n - y_n/C_{x \to y}\big ]^{\rm 2}={\rm Minimum}.$$

2D-WDF  $f_{XY}(x, y)$  sowie die zugehörigen Randwahrscheinlichkeitsdichten  $f_{X}(x)$  und  $f_{Y}(y)$

$\text{Beispiel 2:}$  Es gelten die gleichen Voraussetzungen wie im  $\text{Beispiel 1}$  und es werden auch die dort gefundenen Ergebnisse verwendet.

In der oberen Grafik ist die Regressionsgerade  $R_{x \to y}$  als blaue Kurve eingezeichnet:

• Hierfür ergibt sich  $C_{x \to y}=\mu_{XY}/{\sigma_Y^2} = 1$  und dementsprechend  $\theta_{x \to y}={\rm arctan}\ (1) = 45^\circ.$
• Für den mittleren Abstand aller vier Punkte  $(x_n, y_n )$  von der Regressionsgeraden $R_{x \to y}$  in  $x$–Richtung erhält man unter Ausnutzung der Symmetrie (beachten Sie die blaue Horizontale):

$${\rm MQA}_X = {\rm E} \big [ x_n - y_n/C_{x \to y}\big ]^2 = 2 \cdot \big [ 0.2 \cdot \left [1 - 1/1\right ]^{\rm 2} +0.3 \cdot \left [0.5 - 0/1\right ]^{\rm 2}\big ]=0.15.$$

• Jede Gerade mit einem anderen Winkel als  $45^\circ$  führt hier zu einem größeren  ${\rm MQA}_X$.

Betrachten wir nun die rote Regressionsgerade  $R_{y \to x}$  in der unteren Grafik.

• Hierfür ergibt sich  $C_{y \to x}=\mu_{XY}/{\sigma_X^2} = 0.4/0.55\approx0.727$  und  $\theta_{y \to x}={\rm arctan}\ (0.727) \approx 36^\circ.$
• Hier ist nun der mittlere Abstand der vier Punkte  $(x_n, y_n )$  von der Regressionsgeraden $R_{y \to x}$  in  $y$–Richtung minimal (beachten Sie die roten Vertikalen):

$${\rm MQA}_Y = {\rm E} \big [ y_n - C_{y \to x} \cdot x_n\big ]^2 = 2 \cdot \big [ 0.2 \cdot \left [1 - 0.727 \cdot 1\right ]^{\rm 2} +0.3 \cdot \left [0 - 0.727 \cdot 0.5 \right ]^{\rm 2}\big ]\approx 0.109.$$

Die im Text erwähnte „Korrelationsgerade” mit der Eigenschaft, dass der mittlere quadratische Euklidische Abstand  $\rm (MQA)$  aller Punkte von dieser Geraden minimal ist, wird mit Sicherheit zwischen den beiden hier berechneten Regressionsgeraden liegen.

Versuchsdurchführung

Eventuell noch überarbeiten

• Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
• Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
• Lösung nach Drücken von „Hide solution”.
• Aufgabenstellung und Lösung in Englisch.

Die Nummer 0 entspricht einem „Reset”:

• Gleiche Einstellung wie beim Programmstart.
• Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.

Ende Überarbeitung Voreinstellung für Nummer 0 wie bei den Beispielen vorne

In den folgenden Aufgabenbeschreibungen werden folgende Kurzbezeichnungen verwendet:

• Rot:     Regressionsgerade  $R_{y \to x}$  (im Applet rot gezeichnet),
• Blau:   Regressionsgerade  $R_{x \to y}$  (im Applet blau gezeichnet).

(1)  Mit welcher Parametereinstellung sind die beiden Regressionsgerade  $R_{y \to x}$  und  $R_{x \to y}$  deckungsgleich?

•  Es ist offensichtlich, dass gleiche Regressionsgerade nur möglich sind, wenn diese unter dem Winkel  $45^\circ$  verlaufen   ⇒   „Winkelhalbierende”.
•  Da die fest vorgegebenen Punkte  $3$  und  $4$  auf der Winkelhalbierenden liegen, muss dies auch für die Punkte  $1$  und  $2$  gelten   ⇒   $y_1 = x_1$.
•  Dies gilt für alle Parametereinstellungen  $y_1 = x_1$  und auch für alle  $p_1$  im erlaubten Bereich von   $0$  bis  $0.5$.

(2)  Nun gelte $x_1 = 0.5, y_1 = 0, p_1 = 0.3$  Interpretieren Sie die Ergebnisse.  Aktivieren Sie hierzu die Hilfsgerade.

•  Diese Einstellung stimmt mit den Voraussetzungen von  $\text{Beispiel 1}$  und  $\text{Beispiel 2}$  überein.  Insbesondere gilt  $\theta_{x \to y}= 45^\circ.$  und  $\theta_{y \to x}\approx 36^\circ$.
•  Durch Variation des Winkels  $\theta_{\rm H}$  erkennt man, dass tatsächlich für  $\theta_{\rm H}= 45^\circ$  die Kenngröße  ${\rm MQA}_X =0.15$  den kleinsmöglichen Wert annimmt.
•  Ebenso ergibt sich der kleinsmöglicher Abstand  ${\rm MQA}_Y =0.109$  in  $y$–Richtung für  $\theta_{\rm H}= 36^\circ$, also entsprechend der Regressionsgeraden    $R_{y \to x}$.

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder } {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$.

$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158.$

(3)  Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2;$

$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$

(4)  Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.

Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;

$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;

(5)  Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exakt)}$.

$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0 \ ( \approx 0)$

$\hspace{1.85cm} \text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16}/{16!}\approx 2 \cdot 10^{-22}$.

(6)  Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$

$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$

Zur Handhabung des Applets

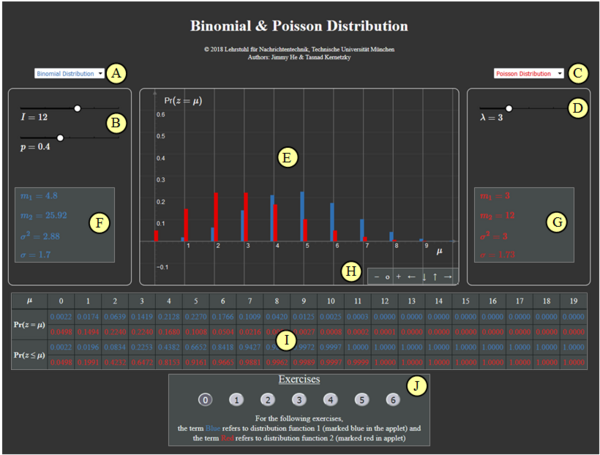
    (A)     Vorauswahl für blauen Parametersatz

    (B)     Parametereingabe $I$ und $p$ per Slider

    (C)     Vorauswahl für roten Parametersatz

    (D)     Parametereingabe $\lambda$ per Slider

    (E)     Graphische Darstellung der Verteilungen

    (F)     Momentenausgabe für blauen Parametersatz

    (G)     Momentenausgabe für roten Parametersatz

    (H)     Variation der grafischen Darstellung

$\hspace{1.5cm}$„$+$” (Vergrößern),

$\hspace{1.5cm}$ „$-$” (Verkleinern)

$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)

$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.

    ( I )     Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$

    (J)     Bereich für die Versuchsdurchführung

Andere Möglichkeiten zur Variation der grafischen Darstellung:

• Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
• Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in a new tab