Exercise 2.3: DSB-AM Realization
Zur Realisierung der so genannten „ZSB–AM mit Träger” soll ein Verstärker mit der Kennlinie
- $$y = g(x) = U \cdot \left( 1 -{\rm e} ^{-x/U}\right)$$
verwendet werden. Hierbei sind $x = x(t)$ und $y = y(t)$ als zeitabhängige Spannungen am Eingang bzw. Ausgang des Verstärkers zu verstehen. Der Parameter $U = 3 \ \rm V$ gibt die Sättigungsspannung des Verstärkers an.
Diese Kennlinie wird im Arbeitspunkt $A_0 = 2\ \rm V$ betrieben. Dies erreicht man beispielsweise durch das Eingangssignal
- $$x(t) = A_0 + z(t) + q(t)\hspace{0.05cm}.$$
Setzen Sie für das Trägersignal und das Quellensignal jeweils Cosinusschwingungen voraus:
- $$ z(t) = A_{\rm T} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} A_{\rm T} = 1\,{\rm V},\hspace{0.2cm} f_{\rm T} = 30\,{\rm kHz},$$
- $$ q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} A_{\rm N} = 1\,{\rm V},\hspace{0.2cm} f_{\rm N} = 3\,{\rm kHz}\hspace{0.05cm}.$$
Verwenden Sie bei der Lösung dieser Aufgabe die Hilfsgröße
- $$w(t) = x(t) - A_0 = z(t) + q(t)\hspace{0.05cm}.$$
Die nichtlineare Kennlinie kann entsprechend einer Taylorreihe um den Arbeitspunkt entwickelt werden:
- $$y(x) = y(A_0) + \frac{1}{1!} \cdot y\hspace{0.08cm}{\rm '}(A_0) \cdot (x - A_0)+ \frac{1}{2!} \cdot y\hspace{0.08cm}''(A_0) \cdot (x - A_0)^2+ \frac{1}{3!} \cdot y\hspace{0.08cm}'''(A_0) \cdot (x - A_0)^3 + \text{ ...}$$
In Abhängigkeit der Hilfsgröße $w(t)$ kann das Ausgangssignal dann auch wie folgt dargestellt werden:
- $$y(t) = c_0 + c_1 \cdot w(t) + c_2 \cdot w^2(t)+ c_3 \cdot w^3(t) +\text{ ...}$$
Das ZSB–AM–Signal $s(t)$ erhält man durch die Bandbegrenzung von $y(t)$ auf den Frequenzbereich von $\text{23 kHz}$ bis $\text{37 kHz}$. Das heißt: Alle anderen Frequenzen als $f_{\rm T}$, $f_{\rm T}±f_{\rm N}$ sowie $f_{\rm T}±2f_{\rm N}$ werden durch den Bandpass entfernt.
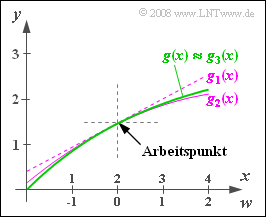
Die Grafik zeigt die Kennlinie $g(x)$ sowie die Näherungen $g_1(x)$, $g_2(x)$ und $g_3(x)$, wenn man die Taylorreihe nach dem ersten, zweiten oder dritten Term abbricht. Man erkennt, dass die Näherung $g_3(x)$ im dargestellten Bereich innerhalb der Zeichengenauigkeit von $g(x)$ nicht mehr zu unterscheiden ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
- Bezug genommen wird auch auf das Kapitel Beschreibung nichtlinearer Systeme im Buch „Lineare zeitinvariante Systeme”.
Fragebogen
Musterlösung
- Die Hilfsgröße $w(t)$ kann somit Werte zwischen $w_{\rm min}\hspace{0.15cm}\underline{ = -2 \ \rm V}$ und $w_{\rm max}\hspace{0.15cm}\underline{ = +2 \ \rm V}$ annehmen.
(2) Der Koeffizient $c_0$ ist gleich dem Kennlinienwert im Arbeitspunkt. Mit $A_0 = 2 \ \rm V$ und $U = 3 \ \rm V$ erhält man:
- $$c_0 = y(A_0) = U \cdot \left( 1 -{\rm e} ^{-A_0/U}\right) \hspace{0.15cm}\underline {= 1.460\,{\rm V}}\hspace{0.05cm}.$$
- Entsprechend gilt für den Taylorkoeffizienten $c_1$:
- $$c_1 = y\hspace{0.06cm}'(A_0)= {\rm e} ^{-A_0/U}\hspace{0.15cm}\underline { = 0.513}\hspace{0.05cm}.$$
(3) Die weiteren Ableitungen $(n ≥ 2)$ lauten:
- $$y^{(n)}(A_0)= \frac{(-1)^{n-1}}{U^{n-1}} \cdot {\rm e} ^{-A_0/U} \hspace{0.05cm}.$$
- Daraus ergeben sich folgende Koeffizienten:
- $$ c_2 = \frac{1}{2!} \cdot y^{(2)}(A_0)= \frac{1}{2U} \cdot {\rm e}^{-A_0/U} \hspace{0.15cm}\underline {= -0.086\,{\rm V^{-1}}}\hspace{0.05cm},$$
- $$c_3 = \frac{1}{3!} \cdot y^{(3)}(A_0)= \frac{1}{6U^2} \cdot {\rm e}^{-A_0/U}\hspace{0.15cm}\underline { = 0.0095\,{\rm V^{-2}}}\hspace{0.05cm}.$$
(4) Setzt man $c_3 = 0$, so lautet das Ausgangssignal des Verstärkers:
- $$y(t) = c_0 + c_1 \cdot (z(t) + q(t)) + c_2 \cdot (z^2(t) + q^2(t) + 2 \cdot z(t) \cdot q(t))\hspace{0.05cm}.$$
- Nach dem Bandpass verbleiben somit noch folgende Signalanteile:
- $$s(t) = c_1 \cdot z(t) + 2 \cdot c_2 \cdot z(t) \cdot q(t) = \left[c_1 \cdot A_{\rm T} + 2 \cdot c_2 \cdot A_{\rm T} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} t)\right] \cdot \cos(\omega_{\rm T} t)\hspace{0.05cm}.$$
- Der Modulationsgrad ist dann als Quotient der „Amplitude” der Nachrichtenschwingung zur „Amplitude” des Trägers zu bestimmen:
- $$m = \frac{2 \cdot |c_2| \cdot A_{\rm T} \cdot A_{\rm N}}{|c_1| \cdot A_{\rm T}} = \frac{2 \cdot |c_2| \cdot A_{\rm N}}{|c_1| }= \frac{2 \cdot 0.086 \cdot 1\,{\rm V}}{0.513 }\hspace{0.15cm}\underline { = 0.335}\hspace{0.05cm}.$$
(5) Richtig sind die Aussagen 2 und 3:
- Unter Berücksichtigung des kubischen Anteils beinhaltet $y(t)$ noch folgende weitere Anteile:
- $$y_3(t) = c_3 \cdot (z(t) + q(t))^3 = c_3 \cdot z^3(t) + 3 \cdot c_3 \cdot z^2(t) \cdot q(t)+ 3 \cdot c_3 \cdot z(t) \cdot q^2(t) + c_3 \cdot q^3(t) \hspace{0.05cm}.$$
- Der erste Term führt zu Anteilen bei $f_{\rm T}$ und $3f_{\rm T}$, der letzte bei $f_{\rm N}$ und $3f_{\rm N}$. Der zweite Term ergibt einen Anteil bei $f_{\rm N}$ und weitere bei $2f_{\rm T} ± f_{\rm N}$:
- $$3 \cdot c_3 \cdot z^2(t) \cdot q(t)= {3}/{2 } \cdot A_{\rm T}^2 \cdot A_{\rm N} \cdot \left[ \cos(\omega_{\rm N} t) + \cos(2\omega_{\rm T} t) \cdot \cos(\omega_{\rm N} t)\right] \hspace{0.05cm}.$$
- Entsprechend führt der dritte Summand in obiger Gleichung zu
- $$3 \cdot c_3 \cdot z(t) \cdot q^2(t)= {3}/{2 } \cdot A_{\rm T} \cdot A_{\rm N}^2 \cdot \left[ \cos(\omega_{\rm T} t) + \cos(\omega_{\rm T} t)\cdot \cos(2 \omega_{\rm N} t)\right] \hspace{0.05cm}.$$
- Innerhalb des Frequenzbereichs von $\text{23 kHz}$ bis $\text{37 kHz}$ kommt es also tatsächlich zu einer Veränderung der Spektrallinie bei $f_{\rm T}$ und es entstehen neue Diraclinien bei $f_{\rm T} ± 2f_{\rm N}$, also bei $\text{24 kHz}$ und $\text{36 kHz}$.
- Die dadurch verbundenen Verzerrungen sind somit nichtlinear ⇒ Antwort 3 ist richtig und Antwort 4 ist falsch.