Exercise 1.1Z: Simple Path Loss Model

• Return to book

Bandbreitenorganisation bei DSL

Radio transmission with line-of-sight can be described by the so-called path loss model, which is given by the following equations: $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$ $$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$

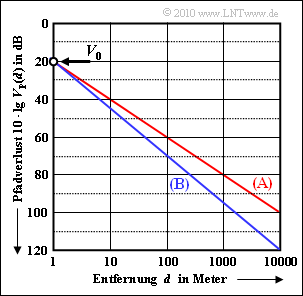
The graphic shows the path loss  $V_{\rm P}(d)$  in  $\rm dB$. The abscissa  $d$  is also displayed logarithmically.

In the above equation, the following parameters are used:

• the distance  $d$  of transmitter and receiver,
• the reference distance  $d_0 = 1 \ \rm m$,
• the path loss exponent  $\gamma$,
• the wavelength  $\lambda$  of the electromagnetic wave.

Two scenarios are shown  $\rm (A)$  and  $\rm (B)$  with the same path loss at distance  $d_0 = 1 \ \rm m$: $$V_{\rm 0} = V_{\rm P}(d = d_0) = 20\,{\rm dB} \hspace{0.05cm}.$$

One of these two scenarios describes the so-called free space attenuation, characterized by the path loss exponent  $\gamma = 2$. However, the equation for the free space attenuation only applies in the far-field, i.e. when the distance  $d$  between transmitter and receiver is greater than the Fraunhofer distance; $$d_{\rm F} = {2 D^2}/{\lambda} \hspace{0.05cm}.$$

Here,  $D$  is the largest physical dimension of the transmitting antenna. With an  $\lambda/2$–antenna, the Fraunhofer distance has a simple expression: $$d_{\rm F} = \frac{2 \cdot (\lambda/2)^2}{\lambda} = {\lambda}/{2}\hspace{0.05cm}.$$

Notes:

• The task belongs to the chapter  Distance-dependent attenuation and shading.
• The speed of light is  $c = 3 \cdot 10^8 \ {\rm m/s}$.

Questionnaire

1

Which path loss exponents apply to the scenarios  $\rm (A)$  and  $\rm (B)$?

$\gamma_{\rm A}\ = \ $

$\gamma_{\rm B} \ = \ $

2

Which scenario describes the free space attenuation?

	scenario  $\rm (A)$,
	Scenario  $\rm (B)$.

3

Which signal frequencies are the basis for the scenarios  $\rm (A)$  and  $\rm (B)$ ?

$f_{\rm A} \ = \ $ $\ \ \rm MHz$

$f_{\rm B} \ = \ $ $\ \ \rm MHz$

Does the free space&ndash scenario apply to all distances between  $1 \ \ \rm m$  and  $10 \ \rm km$?

|type="()"}

+ Yes,

- No.

Sample solution

Solution

'(1)  The (simplest) path loss equation is $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm}.$$

• In scenario (A), the waste per decade (for example, between $d_0 = 1 \ \rm m$ and $d = 10 \ \rm m$) is exactly $20 \ \rm dB$ and in scenario (B) $25 \ \rm dB$.
• It follows:

$$\gamma_{\rm A} \hspace{0.15cm} \underline{= 2}\hspace{0.05cm},\hspace{0.2cm}\gamma_{\rm B} \hspace{0.15cm} \underline{= 2.5}\hspace{0.05cm}.$$

(2)  Correct is solution 1, since the free space attenuation is characterized by the path loss exponent $\gamma = 2$.

(3)  The path loss at $d_0 = 1 \ \rm m$ is in both cases $V_0 = 20 \ \rm dB$. For scenario (A) the same applies: $$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}}\right ]^2 = 20\,{\rm dB} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm A}} = 10 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \lambda_{\rm A} = 4 \pi \cdot 0.1\,{\rm m} = 1,257\,{\rm m} \hspace{0.05cm}.$$

• The frequency $f_{\rm A}$ is related to the wavelength $\lambda_{\rm A}$ over the speed of light $c$:

$$f_{\rm A} = \frac{c}{\lambda_{\rm A}} = \frac{3 \cdot 10^8\,{\rm m/s}}}{1.257\,{\rm m}} = 2.39 \cdot 10^8\,{\rm Hz} \hspace{0.15cm} \underline{\approx 240 \,\,{\rm MHz}} \hspace{0.05cm}.$$

• On the other hand, the scenario (B)

$$10 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ]^{2.5} = 20\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 25 \cdot {\rm lg}\hspace{0.1cm} \left [ \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}}\right ] = 20\,{\rm dB}$$ $$\Rightarrow \hspace{0.3cm} \frac{4 \cdot \pi \cdot d_0}{\lambda_{\rm B}} = 10^{0.8} \approx 6.31 \hspace {0.3cm} \Rightarrow \hspace{0.3cm} {\lambda_{\rm B}} = \frac{10}{6.31} \cdot {\lambda_{\rm A}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {f_{\rm B}}} = \frac{6.31}{10} \cdot {f_{\rm A}}} = 0.631 \cdot 240 \,{\rm MHz}\hspace{0.15cm} \underline {\approx 151.4 \,\,{\rm MHz}} \hspace{0.05cm}.$$

(4)  first suggested solution is correct:

• In free space–scenario (A) the Fraunhofer–distance  $d_{\rm F} = \lambda_{\rm A}/2 \approx 63 \ \rm cm$. Thus, the following always applies  $d > d_{\rm F}$.
• Also in scenario (B) is because of  $\lambda_{\rm B} \approx 2 \ \rm m$  or  $d_{\rm F} \approx 1 \ \rm m$  the entire displayed course correct.