Exercise 3.5Z: Phase Modulation of a Trapezoidal Signal

• Return to book

Trapez– und Rechtecksignal

Ein Phasenmodulator mit dem Eingangssignal  $q_1(t)$  und dem modulierten Signal  $s(t)$  am Ausgang wird durch folgende Gleichung beschrieben:

$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.05cm}\big[\psi(t) \big ]= A_{\rm T} \cdot \cos \hspace{-0.05cm}\big[\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q_1(t) \big ] \hspace{0.05cm}.$$

• Die Trägerkreisfrequenz beträgt  $ω_{\rm T} = 2π · 10^5 \cdot {1}/{\rm s}$.
• Die Augenblickskreisfrequenz  $ω_{\rm A}(t)$  ist gleich der Ableitung der Winkelfunktion  $ψ(t)$  nach der Zeit.
• Die Augenblicksfrequenz ist dann  $f_{\rm A}(t) = ω_{\rm A}(t)/2π$.

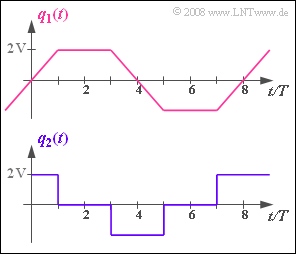
Als Testsignal wird das Trapez–Signal  $q_1(t)$  angelegt, wobei die Nomierungszeitdauer  $T = 10 \ \rm µ s$  beträgt.

Zum gleichen modulierten Signal  $s(t)$  würde ein Frequenzmodulator mit der Winkelfunktion

$$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q_2(t)\hspace{0.15cm}{\rm d}t$$

führen, wenn das rechteckförmige Quellensignal  $q_2(t)$  entsprechend der unteren Skizze angelegt wird.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Frequenzmodulation.
• Bezug genommen wird aber auch auf das Kapitel  Phasenmodulation.

Fragebogen

1

Wie ist die Modulatorkonstante  $K_{\rm PM}$  zu wählen, damit  $ϕ_{\rm max} = 3 \ \rm rad$  beträgt?

$K_{\rm PM} \ = \ $ $\ \rm V^{-1}$

2

Welchen Wertebereich nimmt die Augenblicksfrequenz  $f_{\rm A}(t)$  im Zeitintervall  $0 < t < T$  an?

$f_\text{A, min} \ = \ $ $\ \rm kHz$

$f_\text{A, max} \hspace{0.06cm} = \ $ $\ \rm kHz$

3

Welchen Wertebereich nimmt die Augenblicksfrequenz  $f_{\rm A}(t)$  im Zeitintervall  $T < t < 3T$  an?

$f_\text{A, min} \ = \ $ $\ \rm kHz$

$f_\text{A, max} \hspace{0.06cm} = \ $ $\ \rm kHz$

4

Welchen Wertebereich nimmt die Augenblicksfrequenz  $f_{\rm A}(t)$  im Zeitintervall  $3T < t < 5T$  an?

$f_\text{A, min} \ = \ $ $\ \rm kHz$

$f_\text{A, max} \hspace{0.06cm} = \ $ $\ \rm kHz$

5

Wie muss die Modulatorkonstante  $K_{\rm FM}$  gewählt werden, damit das Signal  $q_2(t)$  nach Frequenzmodulation zum gleichen HF–Signal  $s(t)$  führt?

$K_{\rm FM} \ = \ $ $\ \cdot 10^5 \ \rm V^{-1}s^{-1}$

Musterlösung

Solution

(1)  Die Phasenfunktion berechnet sich zu  $ϕ(t) = K_{\rm PM} · q_1(t)$.  Der Phasenhub  $ϕ_{\rm max}$  ist gleich der sich ergebenden Phase für den Maximalwert des Quellensignals:

$$\phi_{\rm max} = K_{\rm PM} \cdot 2\,{\rm V} = 3\,{\rm rad}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm PM} \hspace{0.15cm}\underline {= 1.5\,{\rm V^{-1}}} \hspace{0.05cm}.$$

(2)  Im Bereich  $0 < t < T$  kann die Winkelfunktion wie folgt dargestellt werden:

$$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm PM} \cdot 2\,{\rm V} \cdot {t}/{T}\hspace{0.05cm}.$$

• Für die Augenblickskreisfrequenz  $ω_{\rm A}(t)$  bzw. die Augenblicksfrequenz  $f_{\rm A}(t)$  gilt dann:

$$\omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}= \omega_{\rm T} + K_{\rm PM} \cdot \frac{2\,{\rm V}}{10\,{\rm µ s}}\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T} + \frac{1.5\,{\rm V}^{-1}}{2 \pi} \cdot 2 \cdot 10^5 \rm {V}/{ s} = 100\,{\rm kHz}+ 47.7\,{\rm kHz}= 147.7\,{\rm kHz}\hspace{0.05cm}.$$

• Die Augenblicksfrequenz ist konstant, so dass  $f_\text{A, min} = f_\text{A, max}\hspace{0.15cm}\underline{ = 147.7 \ \rm kHz}$  gilt.

(3)  Aufgrund des konstanten Quellensignals ist im gesamten hier betrachteten Zeitbereich  $T < t < 3T$  die Ableitung gleich Null, so dass die Augenblicksfrequenz gleich der Trägerfrequenz ist:

$$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} \hspace{0.15cm}\underline {= 100\,{\rm kHz}}\hspace{0.05cm}.$$

(4)  Der lineare Abfall von  $q_1(t)$  im Zeitintervall  $3T < t < 5T$  mit betragsmäßig gleicher Steigung, wie unter Punkt  (2)  berechnet, führt zum Ergebnis:

$$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} - 47.7\,{\rm kHz} \hspace{0.15cm}\underline {= 52.3\,{\rm kHz}}\hspace{0.05cm}.$$

(5)  Durch Differentiation kommt man zur Augenblickskreisfrequenz:

$$\omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q_2(t) \Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T}+\frac{ K_{\rm FM}}{2 \pi} \cdot q_2(t)\hspace{0.05cm}.$$

• Mit dem Ergebnis der Teilaufgabe  (2)  ergibt sich somit:

$$\frac{ K_{\rm FM}}{2 \pi} \cdot 2\,{\rm V} = \frac{ 3 \cdot 10^5}{2 \pi} \cdot {\rm s^{-1}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} \hspace{0.15cm}\underline {= 1.5 \cdot 10^5 \hspace{0.15cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$