Harmonic Oscillation

Definition and Properties

Harmonic oscillations are of particular importance for communications engineering as well as in many natural sciences. The following diagram shows an exemplary signal waveform.

Example of a Harmonic Oscillation

Its importance is also related to the fact that the harmonic oscillation represents the solution of a Differential equation which is found in many disciplines and reads as follows

$$ x(t) + k \cdot\ddot{x} (t) = 0.$$

Here the two dots mark the second derivative of the function $x(t)$ after time.

$\text{Definition:}$ Any harmonic oscillation can be represented in most general form as follows:

$$x(t)= C \cdot \cos(2\pi f_0 t - \varphi).$$

The following signal parameters are used:

the amplitude $C$ – simultaneously the maximum value of the signal,
the signal frequency $f_{0}$ ⇒ the reciprocal of the period duration $T_{0}$, and
the zero phase angle (or briefly the phase) $\varphi$ of the oscillation.

The german learning video Harmonic Oscillations illustrates the properties of harmonic oscillations using scales.

$\text{Comments on nomenclature:}$

In this tutorial - as usual in other literature - when describing harmonic oscillations, Fourier series and Fourier integral, the phase is entered into the equations with a negative sign, whereas in connection with all modulation methods the phase is always entered with a plus sign.
To distinguish between the two variants we use in $\rm LNTwww$ $\varphi$ and $\phi$. Both symbols denote the small Greek "phi". The spelling $\varphi$ is mainly used in the German and $\phi$ in the anglo–american language area.
The indications $\varphi = 90^{\circ}$ and $\phi = -90^{\circ}$ are thus equivalent and both stand for the sine function:

$$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi) = \cos(2 \pi f_0 t + \phi) = \sin(2 \pi f_0 t ).$$

Time Signal Representation

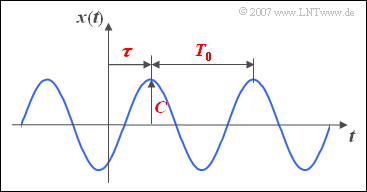
Signal Parameters of a Harmonic Oscillation

The amplitude $C$ can be read directly from the adjacent graphic. The signal frequency $f_0$ is equal to the reciprocal of the period duration $T_0$. If the above equation is written in the form

$$x(t) = C \cdot \cos(2\pi f_0 t - \varphi) = C \cdot \cos \big(2\pi f_0 (t - \tau) \big), $$

it becomes clear that the zero phase angle $\varphi$ and the displacement $\tau$ relative to a cosine signal are related as follows

$$\varphi = \frac{\tau}{T_0} \cdot 2{\pi}. $$

For a cosine signal the parameters $\tau$ and $\varphi$ are zero.
In contrast, a sinusoidal signal is shifted by $\tau = T_0/4$ and accordingly applies to the zero phase angle $\varphi = \pi/2$ (in radians) or $90^{\circ}$.

So it can be stated, that - as assumed for the above sketch - at a positive value of $\tau$ resp. $\varphi$ the $($referring $t = 0)$ nearest signal maximum comes later than at the cosine signal and at negative values earlier. If a cosine signal is present at the system input and the output signal is delayed by a value $\tau$ then the system is called $\tau$ also called the runtime .

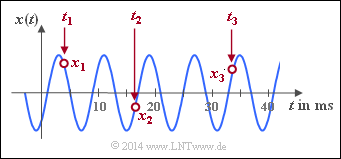
Since a harmonic oscillation is clearly defined by only three signal parameters, the entire time course from $-\infty$ to $+\infty$ can be calculated from only three signal values $x_1=x(t_1)$, $x_2=x(t_2)$, $x_3=x(t_3)$ can be described analytically if the times $t_1$, $t_2$ and $t_3$ have been determined appropriately.

Harmonic Oscillation, defined by
Three Samples

$\text{Example 1:}$ From the three sample values,

$$x_1 = x(t_1 = 3.808 \;{\rm ms}) = +1.609,$$

$$x_2 = x(t_2 = 16.696 \;{\rm ms})=\hspace{0.05 cm} -0.469,$$

$$x_3 = x(t_3 = 33.84 \;{\rm ms}) = +1.227$$

you get the following system of equations:

$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_1 - \varphi) = +1.609\hspace{0.05 cm},$$

$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_2 - \varphi) = \hspace{0.05 cm} -0.469\hspace{0.05 cm},$$

$$C \cdot \cos(2\pi \hspace{0.05 cm} f_0 \hspace{0.05 cm} t_3 - \varphi) = +1.227\hspace{0.05 cm}.$$

After solving this nonlinear system of equations the following signal parameters are obtained:

Signal amplitude $C = 2$,
Period duration $T_0 = 8 \;{\rm ms}$ ⇒ Signal frequency $f_0 = 125 \;{\rm Hz}$,
displacement with respect to a cosine $\tau = 3 \;{\rm ms}$ ⇒ zero phase angle $\varphi = 3\pi /4 = 135^\circ$.

Note: If you set all sampling times $t_1$, $t_2$, $t_3$ in maxima, minima and/or zeros, there is no unique solution for the nonlinear system of equations.

Representation with Cosine and Sine Components

Another representation of the harmonic oscillation is as follows:

$$x(t)=A\cdot\cos(2\pi f_0 t)+ B\cdot\sin(2\pi f_0 t).$$

The terms $A$ and $B$ for the amplitudes of the cosine and sine components are chosen to match the nomenclature of the following chapter Fourier Series .

By applying trigonometric transformations we obtain from the illustration on the last page

$$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)=C\cdot\cos(\varphi)\cdot\cos(2\pi f_0 t)+C\cdot\sin(\varphi)\cdot\sin(2\pi f_0 t).$$

From this follows directly by equating the coefficients:

$$A=C\cdot\cos(\varphi),\hspace{0.5cm}B=C\cdot\sin(\varphi).$$

The magnitude and the zero phase angle of the harmonic oscillation can be calculated from the parameters $A$ and $B$ also according to simple trigonometric considerations

$$C=\sqrt{A^2+B^2}, \hspace{0.5 cm}\varphi = \arctan\left({-B}/{A}\right).$$

$\text{Please consider:}$ The minus-sign at the calculation of the zero-phase-angle $\varphi$ is related to the fact, that $\varphi$ enters the argument of the cosine function with a negative sign.

If one would use the notation "$\cos(2\pi f_0 t - +\phi)$" instead of "$\cos(2\pi f_0 t - \varphi)$" , then $\phi= \arctan(B/A)$. Note the following here:

For Fourier series and Fourier integral, the $\varphi$ representation is common in literature.
For the description of the modulation methods, however, the $\phi$ representation is almost always used.

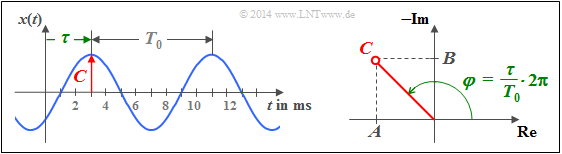
Harmonic oscillation, represented in the complex plane

$\text{Example 2:}$ The oscillation shown in the left graphic as time course is characterized by the parameters

$f_0 = 125 \;{\rm Hz}$,
$\varphi = +135^{\circ}$ ⇒ $\phi = -135^{\circ}$ .

The oscillation is completely described by each of the two equations:

$$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} 2\cdot \cos(2\pi f_0 t-135^{\circ})\hspace{0.05cm},$$

$$x(t) \hspace{-0.05cm}=\hspace{-0.05cm} -\sqrt{2}\cdot \cos(2\pi f_0 t) \hspace{-0.05cm}+\hspace{-0.05cm}\sqrt{2}\cdot \sin(2\pi f_0 t)\hspace{0.05cm}.$$

The right sketch illustrates the trigonometric transformation:

$$A = 2\cdot \cos(-135^{\circ}) = -\sqrt{2}\hspace{0.05cm},$$

$$B = 2\cdot \sin(-135^{\circ}) = +\sqrt{2}\hspace{0.05cm}.$$

Spectral Representation of a Cosine Signal

In order to derive the spectral function, we first restrict ourselves to a cosine signal, which can be written with the complex exponential function and the Euler Theorem also in the following manner:

$$x(t)=A \cdot \cos(2\pi f_0 t)={A}/{2}\cdot \big [{\rm e}^{\rm -j2 \pi \it f_{\rm 0} t} + {\rm e}^{\rm j2\pi \it f_{\rm 0} t} \big ].$$

From this time domain representation it can already be seen that the cosine signal - spectrally seen - contains only one single (physical) frequency, namely the frequency $f_0$.

$\text{Proof:}$ For the mathematical derivation of the spectral function we use the following relations:

the one on the page Dirac Function in Frequency Domain derived functinal relation

$$x(t)=A \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)=A \cdot \rm \delta (\it f).$$

the Displacement theorem (for the frequency range) in anticipation of a later chapter:

$$x(t) \cdot {\rm e}^{\rm j2\pi\it f_{\rm 0} t}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f-f_0). $$

This results in the following Fourier correspondence:

$$x(t)=A\cdot \cos(2\pi f_0t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)={A}/{\rm 2}\cdot {\rm \delta} (f+f_{\rm 0})+{A}/{\rm 2}\cdot {\rm \delta}(\ f-f_{\rm 0}).$$

This means:

The spectral function $X(f)$ of a cosine signal with the frequency $f_0$ is composed of two Dirac functions at $\pm f_0$ .
The pulse weights are each equal to half the signal amplitude.

Spectrum of a cosine signal

$\text{Example 3:}$ The diagram shows the spectrum of a cosine oscillation

with amplitude $A = 4 \;{\rm V}$ and
the frequency $f_0 = 5 \;{\rm kHz}$ ⇒ $T_0 = 200 \;{\rm µ s}$.

Then the following relation to the above equation applies:

The Dirac function at $-f_0$ belongs to the first term $($derivable from the condition $f + f_0 = 0)$.
The Dirac function for $+f_0$ belongs to the second term $($derivable from the condition $f - f_0 = 0)$.
The impulse weights are $A/2 = 2 \;{\rm V}$.

$\text{Please consider:}$ The spectral function of any real time function except the DC signal has components at both positive and negative frequencies.

This fact, which often causes problems for first-year students, is formally derived from the Euler Theorem .
By extending the frequency range from $f \ge 0$ to the set of real numbers you get from the physical to the mathematical frequency.
However, for a negative frequency the definition is not applicable anymore: You cannot interpret „-5 kHz” as "minus 5000 oscillations per second".

In the process of this course you will find that by complicating this simple subject, more complex matters can later be described very elegantly and simply.

General Spectral Representation

For a sinusoidal signal the theorem of Euler applies in a similar way:

$$x(t)=B\cdot \sin(2 \pi f_0 t)= \frac{\it B}{2 \rm j} \cdot \big [{\rm e}^{+{\rm j} 2 \pi \it f_{\rm 0} t}-{\rm e}^{-\rm j2 \pi \it f_{\rm 0} t}\big ]=\rm j\cdot {\it B}/{2} \cdot \big [{\rm e}^{-j2 \pi \it f_{\rm 0} t}-{\rm e}^{+\rm j2 \pi \it f_{\rm 0} t} \big ] .$$

From this follows for the spectral function, which is now purely imaginary:

$$x(t)=B\cdot \sin(2\pi f_0 t)\;\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\; \ X(f)={\rm j} \cdot \big [ {B}/{2} \cdot \delta (f+f_0)- {B}/{2} \cdot \delta (f-f_0) \big ].$$

Spectrum of a sinusoidal signal

$\text{Example 4:}$ The picture shows the purely imaginary spectral function of a sine wave $x(t)$ with

amplitude $B = 3 \;{\rm V},$
frequency $f_0 = 5\;{\rm kHz},$
phase $\varphi=90^{\circ}$ ⇒ $\phi = -90^{\circ}$.

$\text{Please note}$:

For the positive frequency $(f = +f_0)$ the imaginary part is negative.

The negative frequency $(f = -f_0)$ results in a positive imaginary part.

When the cosine and sine components are superimposed according to the relationship

$$x(t)=A \cdot \cos(2\pi f_0 t) +B \cdot \sin(2 \pi f_0 t)$$

the individual spectral functions also overlap and you get

$$X(f)=\frac{A+{\rm j} \cdot B}{2}\cdot {\rm \delta} (f+f_0)+\frac{A-{\rm j} \cdot B}{2} \cdot \delta (f-f_0).$$

With the amplitude $C$ and the phase $\varphi$ this fourier correlation is

$$x(t)=C\cdot \cos(2\pi f_0 t-\varphi)\ \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ X(f)={C}/{2}\cdot {\rm e}^{{\rm j} \varphi} \cdot \delta(f+f_0) + {C}/{2} \cdot {\rm e}^{\rm{-j} \varphi} \cdot \delta (f-f_0).$$

$\text{One recognizes:}$ The spectral function $X(f)$

is not only defined for positive and negative frequencies,
but it is also complex-valued.

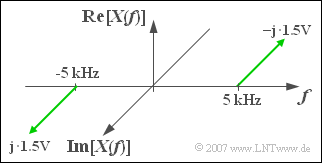
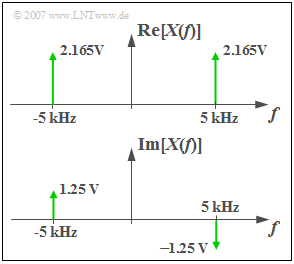
General Spectral Function of a Harmonic Oscillation

$\text{Example 5:}$ With the parameters $C = 5 \;{\rm V}$, $f_0 = 5\;{\rm kHz}$ and $\varphi=90^{\circ}$ $($in radian measure $\pi/6)$ results because

$$2.5 · \cos(30^{\circ}) = 2.165, \hspace{0.3cm} 2.5 · \sin(30^{\circ}) = 1.25$$

The real and/or imaginary part of $X(f)$ according to the graph:

$${\rm Re}\big[X(f)\big]=2.165\,{\rm V} \cdot \delta(f+f_0) + 2.165\,{\rm V} \cdot \delta (f-f_0).$$

$${\rm Im}\big[X(f)\big]=1.25\,{\rm V} \cdot \delta(f+f_0) -1.25\,{\rm V} \cdot \delta (f-f_0).$$

The learning video Harmonic Oscillations (in German) illustrates the properties of harmonic oscillations using the so-called scale.

Exercises for the Chapter

Exercise 2.3: Cosine and Sine Components

Exercise 2.3Z: Oscillation Parameters