Exercise 3.3: From the Signal to the Spectrum
From LNTwww
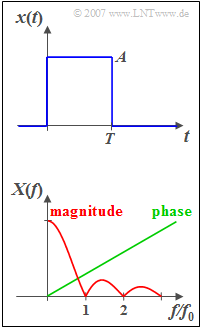
A rectangular pulse $x(t)$ with a duration of $T = 50\,\text{µs}$ and the height of $A = 2\,\text{V}$ is considered. At the jump points at $t = 0$ and $t = T$ the signal value is $A/2$, in each case, but this has no influence on the solution of the task.
In the graphic below, the corresponding spectral function is sketched qualitatively according to magnitude and phase. It is valid:
- $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$
The analytical function progression of $X(f)$ is to be determined.
Hints:
- This exercise belongs to the chapter Special Cases of Impulse Signals.
- The following trigonometric transformations are also given:
- $$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$
Questions
Musterlösung
(1) Mit der Abkürzung $\omega = 2\pi f$ lautet die Spektralfunktion gemäß dem ersten Fourierintegral:
- $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$
- Nach Integration und Einsetzen der Grenzen folgt daraus:
- $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$
- $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$
- Für die Frequenz $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ erhält man:
- $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$
- $${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) Das Betragsquadrat ist die Summe von Real- und Imaginärteil, jeweils quadriert:
- $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$
- Wegen $\sin^2(\alpha) + \cos^2(\alpha) = 1$ kann hierfür auch geschrieben werden:
- $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$
- Setzt man für $\omega = 2\pi f$ und zieht die Wurzel, so erhält man unter der Voraussetzung $A > 0$:
- $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$
- Mit der Abkürzung $\text{si}(x) = \sin(x)/x$ lautet das Ergebnis:
- $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$
- Der Spektralwert bei der Frequenz $f = 1/T = \text{20 kHz}$ ergibt sich zu
- $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$
- Bei der Berechnung des Wertes für $f = 0$ erscheint der Quotient $\text{0 durch 0}$. Durch Anwendung der l'Hospitalschen Regel kann der Grenzwert berechnet werden:
- $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$
- Daraus folgt:
- $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$
- Dieses Ergebnis ist einsichtig, da nach dem ersten Fourierintegral der Spektralwert bei $f = 0$ genau der Fläche unter der Zeitfunktion entspricht.
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Entsprechend dem Ergebnis zur Teilaufgabe (2) treten die Nullstellen im Abstand $f_0 = 1/T$ auf.
- Bei $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ ist zwar der Realteil $0$, aber nicht der Imaginärteil.
- Bei den Argumenten $f \cdot T = 0.5, 1.5, 2.5,\hspace{0.05cm}\text{ ... }$ ist die Sinusfunktion jeweils betragsmäßig gleich $1$, und es gilt:
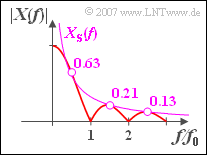
- $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$
- Bei anderen Frequenzen dient $X_{\rm S}(f)$ als obere Schranke, das heißt, es gilt stets $|Xf)| \leq X_{\rm S}(f)$.
- In der Skizze ist diese Schranke zusätzlich zu $|X(f)|$ als violette Kurve eingezeichnet.
(4) Nach der Definition auf der Angabenseite kann man die Phasenfunktion wie folgt berechnen:
- $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$
- Mit den Ergebnissen aus Teilaufgabe (1) gilt somit:
- $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$
- Das Argument dieser Funktion ist entsprechend der Angabe gleich $\tan(\omega T/2) = \tan(\pi fT)$. Daraus folgt ein mit der Frequenz linear ansteigender Verlauf:
- $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$
- Mit $f = 10\,\text{kHz}$ und $T = 50\,\text{µs}$ erhält man daraus den Phasenwinkel $\pi /2$ entsprechend $\underline{90^{\circ}}$ .