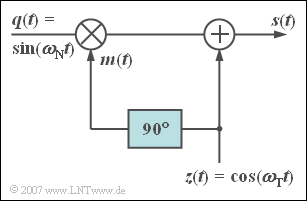
Exercise 4.5Z: Simple Phase Modulator

• Return to book

Modell des betrachteten Phasenmodulators

The diagram shows a quite simple arrangement for approximating a phase modulator. All signals are dimensionless quantities.

The sinusoidal message signal  $q(t)$  of frequency  $f_{\rm N} = 10 \ \text{kHz}$  is multiplied by the signal  $m(t)$ , which results from the cosinusoidal carrier signal  $z(t)$  by phase shifting by  $\phi = 90^\circ$ :

$$m(t) = {\cos} ( \omega_{\rm T} \cdot t + 90^\circ).$$

Then the signal  $z(t)$  with the frequency  $f_{\rm T} = 1 \ \text{MHz}$  is still added directly.

For abbreviation purposes, this task also uses:

• the difference frequency  $f_{\rm \Delta} = f_{\rm T} - f_{\rm N} = 0.99 \ \text{MHz}$,
• the sum frequency  $f_{\rm \Sigma} = f_{\rm T} + f_{\rm N} = 1.01\ \text{MHz}$,
• the two angular frequencies  $\omega_{\rm \Delta} = 2\pi \cdot f_{\rm \Delta}$  and  $\omega_{\rm \Sigma} = 2\pi \cdot f_{\rm \Sigma}$.

Hints:

• This exercise belongs to the chapter  Equivalent Low Pass Signal and Its Spectral Function.

• Consider the trigonomic transformations

$$\sin(\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \sin(\alpha - \beta) + {1}/{2} \cdot \sin(\alpha + \beta),$$

$$\sin(\alpha) \cdot \sin (\beta)= {1}/{2} \cdot \cos(\alpha - \beta) - {1}/{2} \cdot \cos(\alpha + \beta).$$

Questions

1

Which of the following equations correctly describe  $s(t)$ ?

	$s(t) = \cos(\omega_{\rm T} \cdot t) - q(t) \cdot \sin(\omega_{\rm T} \cdot t)$.
	$s(t) = \cos(\omega_{\rm T} \cdot t) + q(t) \cdot \cos(\omega_{\rm T} \cdot t)$.
	$s(t) = \cos(\omega_{\rm T} \cdot t) + 0.5 \sin(\omega_{\rm \Delta} \cdot t) + 0.5 \sin(\omega_{\rm \Sigma} \cdot t)$.
	$s(t) = \cos(\omega_{\rm T} \cdot t) - 0.5 \cos(\omega_{\rm \Delta} \cdot t) + 0.5 \cos(\omega_{\rm \Sigma} \cdot t)$.

2

Calculate the equivalent low pass signal  $s_{\rm TP}(t)$. What are the inphase and quadrature components at time  $t = 0$?

$s_{\rm I}(t = 0)\ = \ $

$s_{\rm Q}(t = 0)\ = \ $

3

Which of the following statements are true for the locus curve  $s_{\rm TP}(t)$ zu?

	The locus curve is a circular arc.
	The locus curve is a horizontal straight line.
	The locus curve is a vertical straight line.

4

Calculate the magnitude  $a(t)$, in particular its maximum and minimum values.

$a_{\rm max}\ = \ $

$a_{\rm min}\ = \ $

Solution

Solution

(1)  The first and last suggestions are correct:

• Due to the phase shift by  $\phi = 90^\circ$  the cosine function becomes the minus-sine function.
• With  $q(t) = \sin(\omega_{\rm N} t)$  holds:

$${s(t)} = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - \sin({ \omega_{\rm T}\hspace{0.05cm} t }) \cdot \sin({ \omega_{\rm N}\hspace{0.05cm} t }) = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - 0.5 \cdot \cos(({ \omega_{\rm T}-\omega_{\rm N})\hspace{0.05cm} t }) + 0.5 \cdot \cos(({ \omega_{\rm T}+\omega_{\rm N})\hspace{0.05cm} t }).$$

(2)  The spectrum of the analytical signal is:

$$S_{\rm +}(f) = \delta (f - f_{\rm T}) - 0.5 \cdot \delta (f - f_{\rm \Delta})+ 0.5 \cdot \delta (f - f_{\rm \Sigma}) .$$

• By shitfing  $f_{\rm T}$  one arrives at the spectrum of the equivalent low pass signal:

$$S_{\rm TP}(f) = \delta (f ) - 0.5 \cdot \delta (f + f_{\rm N})+ 0.5 \cdot \delta (f - f_{\rm N}) .$$

• This leads to the time function

$$s_{\rm TP}(t) = {\rm 1 } - 0.5 \cdot {\rm e}^{{-\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t }+ 0.5 \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t } = 1 + {\rm j} \cdot \sin(\omega_{\rm N} \hspace{0.05cm} t ).$$

• At time  $t = 0$ ist $s_{\rm TP}(t) = 1$, is real. Thus:

• $s_{\rm I}(t = 0) = \text{Re}[s_{\rm TP}(t = 0)]\; \underline{= 1}$,

• $s_{\rm Q}(t = 0) = \text{Ime}[s_{\rm TP}(t = 0)]\; \underline{= 0}$.

Locus curve of a simple phase modulator

(3)  The locus curve is a vertical straight line   ⇒   Proposition 3 with the following values:

$$s_{\rm TP}(t = 0) = s_{\rm TP}(t = {\rm 50 \hspace{0.05cm} µ s}) = \text{ ...} = 1,$$

$$s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 125 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 + {\rm j},$$

$$s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 175 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 - {\rm j}.$$

(4)  The magnitude (the pointer length) varies between   $a_{\rm max} = \sqrt{2}\; \underline{\approx 1.414}$  and  $a_{\rm min} \;\underline{= 1}$. It holds:

$$a(t) = \sqrt{1 + \sin^2(\omega_{\rm N} \hspace{0.05cm} t )}.$$

With ideal phase modulation, on the other hand, the envelope  $a(t)$  would have to be constant.

(5)  The real part is always  $1$, the imaginary part equal to  $\sin(\omega_{\rm N} \cdot t)$. From this follows the phase function:

$$\phi(t)= {\rm arctan} \hspace{0.1cm}{\left(\sin(\omega_{\rm N} \hspace{0.05cm} t )\right)}.$$

• The maximum value of the sine function is  $1$. From this follows:

$$\phi_{\rm max} = \arctan (1) \; \underline{= \pi /4 } \; \Rightarrow \; \underline{45^\circ}.$$