Exercise 5.1: Sampling Theorem

• Return to book

Zur Abtastung eines analogen Signals  $x(t)$

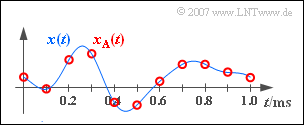
Given is an analogue signal  $x(t)$  according to the sketch:

• It is known that this signal does not contain any frequencies higher than  $B_{\rm NF} = 4 \ \text{kHz}$ .
• By sampling with the sampling rate  $f_{\rm A}$ , the signal  $x_{\rm A}(t)$ sketched in red in the diagram is obtained.
• For signal reconstruction a low-pass filter is used, for whose frequency response applies:

$$H(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_1 \hspace{0.05cm}, \\ |f| > f_2 \hspace{0.05cm} \\ \end{array}$$

The range between the frequencies  $f_1$  and  $f_2 > f_1$  is not relevant for the solution of this task.

The corner frequencies  $f_1$  and  $f_2$  are to be determined in such a way that the output signal  $y(t)$  of the low-pass filter exactly matches the signal  $x(t)$ .

Hints:

• This task belongs to the chapter  Time Discrete Signal Representation.

• There is an interactive applet for the topic dealt with here:  Abtastung periodischer Signale & Signalrekonstruktion

Questions

1

Determine the underlying sampling rate from the graph.

$f_{\rm A}\ = \ $  $\text{kHz}$

2

At which frequencies does the spectral function  $X_{\rm A}(f)$  have no components with certainty?

	$f = 2.5 \ \text{kHz},$
	$f= 5.5 \ \text{kHz},$
	$f= 6.5 \ \text{kHz},$
	$f= 34.5 \ \text{kHz}.$

3

What is the minimum size of the lower cut-off frequency  $f_1$  that the signal is perfectly reconstructed?

$f_{1,\ \text{min}}\ = \ $  $\text{kHz}$

4

What is the maximum size of the upper corner frequency  $f_2$  for the signal to be perfectly reconstructed?

$f_{2,\ \text{max}}\ = \ $  $\text{kHz}$

Solution

Solution

(1)  The distance between two adjacent samples is  $T_{\rm A} = 0.1 \ \text{ms}$. Thus, for the sampling rate  $f_{\rm A} = 1/ T_{\rm A} \;\underline {= 10 \ \text{kHz}}$is obtained.

Spectrum  $X_{\rm A}(f)$  of the sampled signal (schematic representation)

(2)  Proposed solutions 2 and 4 are correct:

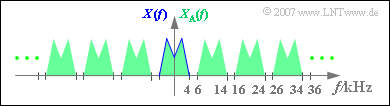
• The spectrum  $X_{\rm A}(f)$  of the sampled signal is obtained from  $X(f)$  by periodic continuation at a distance of  $f_{\rm A} = 10 \ \text{kHz}$.
• From the sketch you can see that  $X_{\rm A}(f)$  can have parts at  $f = 2.5 \ \text{kHz}$  and  $f = 6.5 \ \text{kHz}$ .
• In contrast, there are no components at  $f = 5.5 \ \text{kHz}$ .
• Also at  $f = 34.5 \ \text{kHz}$  will be valid in any case.  $X_{\rm A}(f) = 0$ .

(3)  It must be ensured that all frequencies of the analogue signal are weighted with  $H(f) = 1$ .

• From this follows according to the sketch:

$$f_{1, \ \text{min}} = B_{\rm NF} \;\underline{= 4 \ \text{kHz}}.$$

(4)  Likewise, it must be guaranteed that all spectral components of  $X_{\rm A}(f)$, that are not contained in  $X(f)$  are removed by the low-pass filter.

• According to the sketch, the following must therefore apply:

$$f_{2, \ \text{max}} = f_{\rm A} – B_{\rm NF} \;\underline{= 6 \ \text{kHz}}.$$