Exercise 5.2: Inverse Discrete Fourier Transform

• Return to book

Fünf verschiedene Sätze für die Spektralkoeffizienten  $D(\mu)$

Bei der Diskreten Fouriertransformation  (DFT) werden

• aus den  $N$  Zeitkoeffizienten  $d(\nu)$   ⇒   Abtastwerte des zeitkontinuierlichen Signals  $x(t)$ –
• die  $N$  Spektralbereichskoeffizienten  $D(\mu)$

berechnet. Mit  $\nu = 0$, ... , $N – 1$  und  $\mu = 0$, ... , $N – 1$  gilt:

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

Hierbei bezeichnet  $w$  den komplexen Drehfaktor:

$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$

Für die Inverse Diskrete Fouriertransformation  (IDFT)   ⇒   „Umkehrfunktion” der DFT gilt entsprechend:

$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

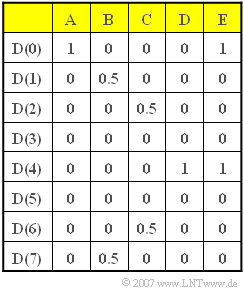
In dieser Aufgabe sollen für verschiedene Beispielfolgen  $D(\mu)$  (die in der obigen Tabelle mit  $\rm A$, ... ,  $\rm E$ bezeichnet sind) die Zeitkoeffizienten  $d(\nu)$  ermittelt werden. Es gilt somit stets  $N = 8$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Diskrete Fouriertransformation (DFT).

• Die hier behandelte Thematik wird auch im interaktiven Applet  Diskrete Fouriertransformation und Inverse behandelt.

Fragebogen

1

Wie lauten die Zeitkoeffizienten  $d(\nu)$  für die  $D(\mu)$–Werte von Spalte  $\rm A$?

$d(0)\ = \ $

$d(1)\ = \ $

2

Wie lauten die Zeitkoeffizienten  $d(ν)$  für die  $D(\mu)$–Werte von Spalte  $\rm B$?

$d(0)\ = \ $

$d(1)\ = \ $

3

Wie lauten die Zeitkoeffizienten  $d(ν)$  für die  $D(\mu)$–Werte von Spalte  $\rm C$?

$d(0)\ = \ $

$d(1)\ = \ $

4

Wie lauten die Zeitkoeffizienten  $d(ν)$  für die  $D(\mu)$–Werte von Spalte  $\rm D$?

$d(0)\ = \ $

$d(1)\ = \ $

5

Wie lauten die Zeitkoeffizienten  $d(ν)$  für die  $D(\mu)$–Werte von Spalte  $\rm E$?

$d(0)\ = \ $

$d(1)\ = \ $

Musterlösung

Solution

(1)  Aus der IDFT–Gleichung wird mit  $D(\mu) = 0$  für  $\mu \ne 0$:

$$d(\nu) = D(0) \cdot w^0 = D(0) =1\hspace{0.5cm}(0 \le \nu \le 7)\ \hspace{0.5cm} \Rightarrow\hspace{0.5cm}\hspace{0.15 cm}\underline{d(0) = d(1) = 1}.$$

• Dieser Parametersatz beschreibt die diskrete Form der Fourierkorrespondenz des Gleichsignals:

$$x(t) = 1 \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {\delta}(f) \hspace{0.05cm}.$$

(2)  Alle Spektralkoeffizienten sind Null mit Ausnahme von  $D_1 = D_7 = 0.5$. Daraus folgt für  $0 ≤ ν ≤ 7$:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} \hspace{0.05cm}.$$

• Aufgrund der Periodizität gilt aber auch:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{4} \cdot \nu \right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) = {1}/{\sqrt{2}} \approx 0.707} \hspace{0.05cm}.$$

• Es handelt sich also um das zeitdiskrete Äquivalent zu

$$x(t) = \cos(2 \pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + f_{\rm A}) + {1}/{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$

wobei  $f_{\rm A}$  die kleinste in der DFT darstellbare Frequenz bezeichnet.

(3)  Gegenüber der Teilaufgabe  (2)  ist nun die Schwingungsfrequenz doppelt so groß, nämlich  $2 f_{\rm A}$  anstelle von  $f_{\rm A}$:

$$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + 2f_{\rm A}) + {1}/{2} \cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$

• Damit beschreibt die Folge  $\langle \hspace{0.1cm}d(ν)\hspace{0.1cm}\rangle$  zwei Perioden der Cosinusschwingung, und es gilt für  $0 ≤ ν ≤ 7$:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{2} \cdot \nu \right)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = 0} \hspace{0.05cm}.$$

(4)  Durch eine weitere Verdoppelung der Cosinusfrequenz auf  $4 f_{\rm A}$  kommt man schließlich zur zeitkontinuierlichen Fourierkorrespondenz

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) \hspace{0.05cm}$$

und damit zu den Zeitkoeffizienten

$$d(0) =d(2) =d(4) =d(6) \hspace{0.15 cm}\underline{= +1}, \hspace{0.2cm}d(1) =d(3) =d(5) =d(7) \hspace{0.15 cm}\underline{= -1} \hspace{0.05cm}.$$

• Zu beachten ist, dass hier die beiden Diracfunktionen in der zeitdiskreten Darstellung aufgrund der Periodizität zusammenfallen.
• Die Koeffizienten  $D (+4) = 0.5$  und  $D (-4) = 0.5$  ergeben zusammen  $D (4) = 1$.

(5)  Die Diskrete Fouriertransformation ist ebenfalls linear. Deshalb ist das Superpositionsprinzip weiterhin anwendbar:

• Die Koeffizienten  $D(\mu )$  aus Spalte  $\rm E$  ergeben sich als die Summen der Spalten  $\rm A$  und  $\rm D$.
• Deshalb wird aus der alternierenden Folge  $\langle \hspace{0.1cm}d(ν) \hspace{0.1cm}\rangle$  entsprechend Teilaufgabe  (4)  die um  $1$  nach oben verschobene Folge:

$$\hspace{0.15 cm}\underline{d(0) =d(2) =d(4) =d(6)= 2}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) =d(3) =d(5) =d(7) = 0} \hspace{0.05cm}.$$