Exercise 5.2: Inverse Discrete Fourier Transform

• Return to book

Five different sets for the spectral coefficients  $D(\mu)$

With the Discrete Fourier Transform  (DFT), the following are obtained

• from the  $N$  time coefficients  $d(\nu)$   ⇒   samples of the continuous-time signal  $x(t)$ –
• the  $N$  spectral range coefficients  $D(\mu)$

are calculated. With  $\nu = 0$, ... , $N – 1$  and  $\mu = 0$, ... , $N – 1$  holds:

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

Here  $w$  denotes the complex rotation factor:

$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$

For the Inverse Discrete Fourier Transform  (IDFT)   ⇒   „inverse function” of the DFT, the following applies accordingly:

$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

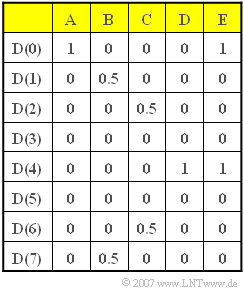
In this task, the time coefficients  $d(\nu)$  are to be determined for various example sequences (which are labelled  $\rm A$, ... ,  $\rm E$ in the table above)  $D(\mu)$  ermittelt werden. Thus,  $N = 8$ always applies.

Hints:

• This task belongs to the chapter  Discrete Fourier Transformation (DFT).

• The topic dealt with here is also dealt with in the interactive applet  Discrete Fourier Transform and Inverse.

Questions

1

What are the time coefficients  $d(\nu)$  for the  $D(\mu)$–values of column  $\rm A$?

$d(0)\ = \ $

$d(1)\ = \ $

2

What are the time coefficients  $d(ν)$  for the  $D(\mu)$–values of column  $\rm B$?

$d(0)\ = \ $

$d(1)\ = \ $

3

What are the time coefficients  $d(ν)$  for the  $D(\mu)$–values of column  $\rm C$?

$d(0)\ = \ $

$d(1)\ = \ $

4

What are the time coefficients  $d(ν)$  for the  $D(\mu)$–values of column  $\rm D$?

$d(0)\ = \ $

$d(1)\ = \ $

5

What are the time coefficients  $d(ν)$  for the  $D(\mu)$–values of column  $\rm E$?

$d(0)\ = \ $

$d(1)\ = \ $

Solution

Solution

(1)  From the IDFT equation, with  $D(\mu) = 0$  for  $\mu \ne 0$:

$$d(\nu) = D(0) \cdot w^0 = D(0) =1\hspace{0.5cm}(0 \le \nu \le 7)\ \hspace{0.5cm} \Rightarrow\hspace{0.5cm}\hspace{0.15 cm}\underline{d(0) = d(1) = 1}.$$

• This set of parameters describes the discrete form of the Fourier correspondence of the DC signal:

$$x(t) = 1 \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {\delta}(f) \hspace{0.05cm}.$$

(2)  All spectral coefficients are zero except  $D_1 = D_7 = 0.5$. It follows for  $0 ≤ ν ≤ 7$:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} \hspace{0.05cm}.$$

• However, due to periodicity, also holds:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{4} \cdot \nu \right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) = {1}/{\sqrt{2}} \approx 0.707} \hspace{0.05cm}.$$

• It is therefore the discrete-time equivalent of

$$x(t) = \cos(2 \pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + f_{\rm A}) + {1}/{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$

where  $f_{\rm A}$  denotes the smallest frequency that can be represented in the DFT.

(3)  Compared to subtask  (2) , the oscillation frequency is now twice as large, namely  $2 f_{\rm A}$  instead of  $f_{\rm A}$:

$$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + 2f_{\rm A}) + {1}/{2} \cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$

• Thus the sequence  $\langle \hspace{0.1cm}d(ν)\hspace{0.1cm}\rangle$  describes two periods of the cosine oscillation, and it holds for  $0 ≤ ν ≤ 7$:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{2} \cdot \nu \right)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = 0} \hspace{0.05cm}.$$

(4)  By further doubling the cosine frequency to  $4 f_{\rm A}$  one finally arrives at the continuous-time Fourier correspondence

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) \hspace{0.05cm}$$

and thus to the time coefficients

$$d(0) =d(2) =d(4) =d(6) \hspace{0.15 cm}\underline{= +1}, \hspace{0.2cm}d(1) =d(3) =d(5) =d(7) \hspace{0.15 cm}\underline{= -1} \hspace{0.05cm}.$$

• Note that here the two Dirac functions coincide in the discrete-time representation due to periodicity.
• The coefficients  $D (+4) = 0.5$  and  $D (-4) = 0.5$  together give  $D (4) = 1$.

(5)  The Discrete Fourier Transform is also linear. Therefore, the superposition principle is still applicable:

• The coefficients  $D(\mu )$  from column  $\rm E$  result as the sums of columns  $\rm A$  and  $\rm D$.
• Therefore, the alternating sequence  $\langle \hspace{0.1cm}d(ν) \hspace{0.1cm}\rangle$  becomes the sequence shifted up by  $1$  according to subtask  (4) :

$$\hspace{0.15 cm}\underline{d(0) =d(2) =d(4) =d(6)= 2}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) =d(3) =d(5) =d(7) = 0} \hspace{0.05cm}.$$